Analyse de corrélation et de régression: exemple, tâches, application. Méthode d'analyse de corrélation et de régression

Analyse de régression de corrélation - C’est l’une des méthodes les plus courantes pour étudier la relation entre les valeurs numériques. Son objectif principal est de trouver la relation entre les deux paramètres et son degré avec la dérivation ultérieure de l'équation. Par exemple, nous avons des étudiants qui ont réussi l'examen de mathématiques et d'anglais. Nous pouvons utiliser la corrélation pour déterminer si le succès d'un test affecte les résultats dans un autre sujet. En ce qui concerne l’analyse de régression, il est utile de prévoir les notes en mathématiques en fonction des points obtenus lors d’un examen d’anglais, et inversement.

Qu'est-ce qu'un tableau de corrélation?

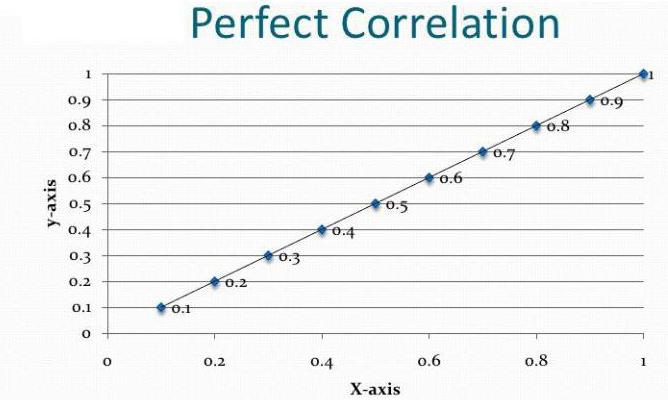
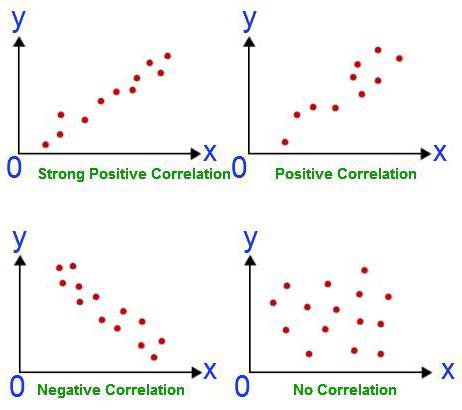
Toute analyse commence par la collecte d'informations. Plus le résultat est élevé, plus le résultat obtenu est précis. Dans l'exemple ci-dessus, nous avons deux disciplines dans lesquelles les étudiants doivent passer un examen. Leur taux de réussite est une estimation. L'analyse de corrélation-régression indique si le résultat d'une matière affecte les points obtenus lors du deuxième examen. Afin de répondre à cette question, il est nécessaire d'analyser les évaluations de tous les étudiants en parallèle. Mais vous devez d’abord choisir la variable dépendante. Dans ce cas, ce n'est pas si important. Supposons qu'un examen de mathématiques ait eu lieu plus tôt. Les points dessus sont une variable indépendante (ils sont reportés en abscisse). L'anglais est à l'horaire plus tard. Par conséquent, les estimations basées sur cette variable constituent une variable dépendante (en ordonnée). Plus le graphique ainsi obtenu ressemble à une ligne droite, plus la corrélation linéaire entre les deux valeurs sélectionnées est forte. Cela signifie que les étudiants en mathématiques sont plus susceptibles d'avoir cinq ans à l'examen d'anglais.

Hypothèses et simplifications

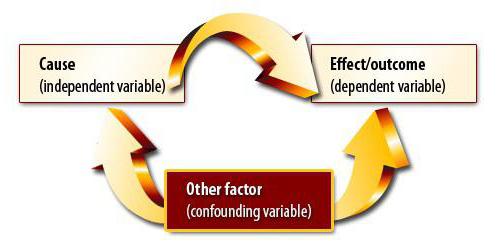
La méthode d'analyse de corrélation et de régression implique la recherche d'une relation de cause à effet. Cependant, à la première étape, vous devez comprendre que les changements dans les deux quantités peuvent être dus à une troisième, non encore prise en compte par le chercheur. Il peut également exister des relations non linéaires entre les variables. L'obtention d'un coefficient égal à zéro n'est donc pas la fin de l'expérience.

Corrélation linéaire de Pearson

Ce coefficient peut être utilisé sous deux conditions. Le premier - toutes les valeurs des variables sont des nombres rationnels, le second - il est prévu que les valeurs changent proportionnellement. Ce coefficient est toujours compris entre -1 et 1. S'il est supérieur à zéro, il existe alors une dépendance directement proportionnelle, moins - inversement égale, égale - ces valeurs ne s'affectent en aucune manière. La possibilité de calculer cet indicateur est la base de l'analyse de corrélation et de régression. Pour la première fois, ce coefficient a été développé par Karl Pearson sur la base de l’idée de Francis Galton.

Propriétés et précautions

Le coefficient de corrélation de Pearson est un outil puissant, mais il convient également de l'utiliser avec prudence. Les avertissements suivants sont utilisés:

1. Le coefficient de Pearson indique la présence ou l'absence d'une relation linéaire. L'analyse de corrélation-régression ne s'arrête pas là, il se peut que les variables soient néanmoins interconnectées.
2. Il faut être prudent dans l'interprétation de la valeur du coefficient. Une corrélation peut être trouvée entre la taille de la jambe et le niveau de QI.Mais cela ne signifie pas qu'un indicateur en détermine un autre.
3. Le coefficient de Pearson ne dit rien sur le lien de causalité entre les indicateurs.

Coefficient de corrélation de rang de Spearman

Si une modification de la valeur d'un indicateur entraîne une augmentation ou une diminution de la valeur d'un autre, cela signifie qu'ils sont liés. L'analyse de corrélation-régression, dont un exemple sera donné ci-dessous, est précisément liée à de tels paramètres. Le coefficient de classement vous permet de simplifier les calculs.

Analyse de corrélation et de régression: un exemple

Supposons qu'il existe une évaluation de l'efficacité de dix entreprises. Nous avons deux juges qui leur donnent des points. L'analyse de corrélation et de régression de l'entreprise dans ce cas ne peut pas être effectuée sur la base du coefficient linéaire de Pearson. Nous ne sommes pas intéressés par la relation entre les notations des juges. Les rangs des entreprises selon les juges sont importants.

Ce type d'analyse présente les avantages suivants:

• Forme non paramétrique des relations entre les quantités étudiées.
• Facilité d'utilisation, car les rangs peuvent être attribués à la fois par ordre croissant de valeur et par ordre décroissant.

La seule exigence de ce type d'analyse est la nécessité de convertir les données source.

Problèmes d'application

L'analyse de corrélation et de régression repose sur les hypothèses suivantes:

• Les observations sont considérées comme indépendantes (une perte de «l'aigle» de cinq fois n'affecte pas le résultat du prochain lancer de pièce).
• Dans l'analyse de corrélation, les deux variables sont considérées comme aléatoires. En régression - un seul (dépendant).
• Lors du test d'une hypothèse, une distribution normale doit être observée. La modification de la variable dépendante doit être la même pour chaque valeur en abscisse.
• Le diagramme de corrélation n'est que le premier test de l'hypothèse sur la relation entre les deux séries de paramètres et non le résultat final de l'analyse.

Dépendance et causalité

Supposons que nous ayons calculé le coefficient de corrélation du volume des exportations et du PIB. Il s'est avéré être égal à l'unité modulo. Avons-nous fait l'analyse de corrélation et de régression jusqu'au bout? Bien sur que non Le résultat obtenu ne signifie nullement que le PIB puisse être exprimé par les exportations. Nous n'avons pas encore prouvé de lien de causalité entre les indicateurs. Analyse de corrélation-régression - prévision des valeurs d'une variable en fonction d'une autre. Cependant, vous devez comprendre que souvent, de nombreux facteurs affectent le paramètre. L'exportation détermine le PIB, mais pas seulement. Il y a d'autres facteurs. Il existe ici une corrélation et un lien de causalité, bien ajusté pour tenir compte des autres composantes du produit intérieur brut.

Une autre situation est beaucoup plus dangereuse. Au Royaume-Uni, une enquête a montré que les enfants dont les parents fumaient étaient plus souvent des délinquants. Cette conclusion repose sur une forte corrélation entre l'indicateur. Mais est-il correct? Premièrement, la dépendance pourrait être inverse. Les parents pourraient commencer à fumer en raison du stress causé par le fait que leurs enfants subissent constamment des modifications et enfreignent la loi. Deuxièmement, les deux paramètres peuvent être dus au troisième. Ces familles appartiennent à des classes sociales basses, caractérisées par les deux problèmes. Par conséquent, sur la base de la corrélation, il n’est pas possible de conclure à un lien de causalité.

Pourquoi utiliser l'analyse de régression?

La corrélation dépend de la recherche de relations entre les quantités. La relation de causalité dans ce cas reste en coulisse. Les tâches d’analyse de corrélation et de régression ne coïncident que pour confirmer l’existence d’une relation entre les valeurs de deux quantités. Cependant, au départ, le chercheur ne fait pas attention à la possibilité d’un lien de causalité. L'analyse de régression a toujours deux variables, dont l'une est dépendante. Il se déroule en plusieurs étapes:

1. Choisir le bon modèle en utilisant la méthode des moindres carrés.
2. Dérivation d'une équation décrivant l'effet d'un changement d'une variable indépendante sur une autre.

Par exemple, si nous étudions l'effet de l'âge sur la croissance humaine, une analyse de régression peut aider à prévoir les changements survenus au cours des années.

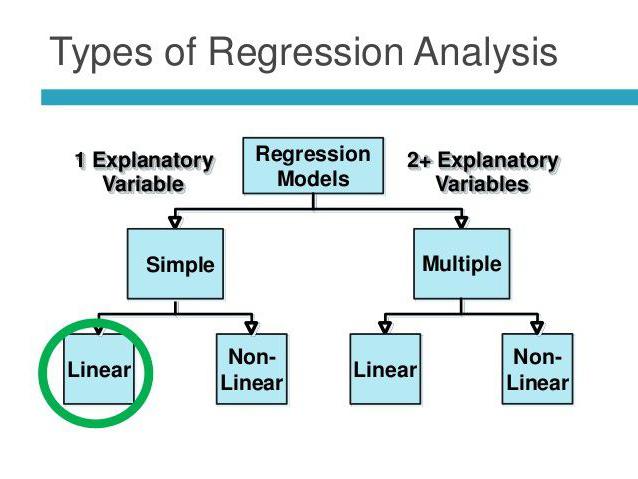
Régression linéaire et multiple

Supposons que X et Y sont deux variables liées. L’analyse de régression nous permet de prédire l’ampleur de l’un en fonction des valeurs de l’autre. Par exemple, la maturité et l’âge sont des symptômes dépendants. La relation entre eux est reflétée par régression linéaire. En fait, vous pouvez exprimer X par Y ou vice versa. Mais souvent, une seule des lignes de régression est correcte. Le succès de l'analyse dépend en grande partie de la détermination correcte de la variable indépendante. Par exemple, nous avons deux indicateurs: le rendement et les précipitations. Au quotidien, il apparaît clairement que le premier dépend du second et non l'inverse.

La régression multiple vous permet de calculer une valeur inconnue en fonction des valeurs de trois variables ou plus. Par exemple, le rendement en riz par acre de terre dépend de la qualité du grain, de la fertilité du sol, des engrais, de la température et des précipitations. Tous ces paramètres affectent le résultat global. Pour simplifier le modèle, les hypothèses suivantes sont utilisées:

• La relation entre les caractéristiques indépendantes et influentes est linéaire.
• La multicolinéarité est exclue. Cela signifie que les variables dépendantes ne sont pas interconnectées.
• Homoscédasticité et normalité des séries de nombres.

L'utilisation de l'analyse de corrélation et de régression

Il y a trois cas principaux d'utilisation de cette méthode:

1. Tester les relations occasionnelles entre les quantités. Dans ce cas, le chercheur détermine les valeurs de la variable et détermine si elles affectent la modification de la variable dépendante. Par exemple, vous pouvez donner aux gens différentes doses d'alcool et mesurer leur tension artérielle. Dans ce cas, le chercheur sait avec certitude que le premier est la cause du second et non l'inverse. L'analyse de corrélation-régression vous permet de détecter une relation linéaire directement proportionnelle entre ces deux variables et de dériver une formule qui la décrit. Dans ce cas, les valeurs exprimées dans des unités de mesure complètement différentes peuvent être comparées.
2. Trouver une relation entre deux variables sans étendre une relation causale à elles. Dans ce cas, il n'y a pas de différence quelle taille le chercheur appelle dépendante. De plus, en réalité, il se peut que la troisième variable affecte les deux. Par conséquent, elles changent proportionnellement.
3. Calcul des valeurs d'une quantité en fonction d'une autre. Il est basé sur une équation dans laquelle des nombres connus sont substitués.

Ainsi, l’analyse de corrélation implique la recherche d’un lien (non causal) entre les variables et l’analyse de régression l’explique, en utilisant souvent une fonction mathématique.