"Stochastik" ist ein Wort, mit dem Physiker, Mathematiker und andere Wissenschaftler zufällige Prozesse beschreiben. Sein Ursprung ist altgriechisch. Übersetzt heißt es "erraten können".
Bedeutung des Wortes "stochastisch"

"Stochastisch" ist ein Konzept, das in vielen verschiedenen Bereichen der Wissenschaft verwendet wird. Es bedeutet Zufälligkeit, Zufälligkeit, Ungewissheit von etwas. In der Ethik des Aristoteles (sein skulpturales Porträt ist oben dargestellt) ist der Begriff „stochastisch“ eine Definition, die sich auf die Fähigkeit bezieht, zu raten. Offensichtlich verwendeten Mathematiker es auf der Grundlage, dass das Element des Zufalls nur dann erscheint, wenn es notwendig ist, zu erraten. Das Wort "stochastisch" ist ein Begriff, der im New International Dictionary als "Vermutung" definiert ist.
Somit kann festgestellt werden, dass die technische Bedeutung dieses Konzepts nicht genau seiner (lexikalischen) Wortschatzbedeutung entspricht. Einige Autoren verwenden den Ausdruck "stochastischer Prozess" als Synonym für den Begriff "zufälliger Prozess".
Stochastizität in der Mathematik

Die Verwendung dieses Begriffs in der Mathematik ist derzeit weit verbreitet. Zum Beispiel gibt es in der Wahrscheinlichkeitstheorie ein solches Konzept wie den stochastischen Prozess. Sein Ergebnis kann vom Ausgangszustand dieses Systems nicht bestimmt werden.
Die Verwendung des Begriffs "Stochastizität" in der Mathematik wird den Werken von Vladislav Bortskevich zugeschrieben. Er benutzte den Begriff im Sinne von "Hypothesen aufstellen". In der Mathematik, insbesondere in einem Bereich dieser Wissenschaft wie der Wahrscheinlichkeitstheorie, spielt das Gebiet der Zufallsforschung eine wichtige Rolle. Es gibt zum Beispiel eine stochastische Matrix. Die Spalten oder Zeilen dieser Matrix addieren sich zu eins.
Stochastische Mathematik (Finanz)
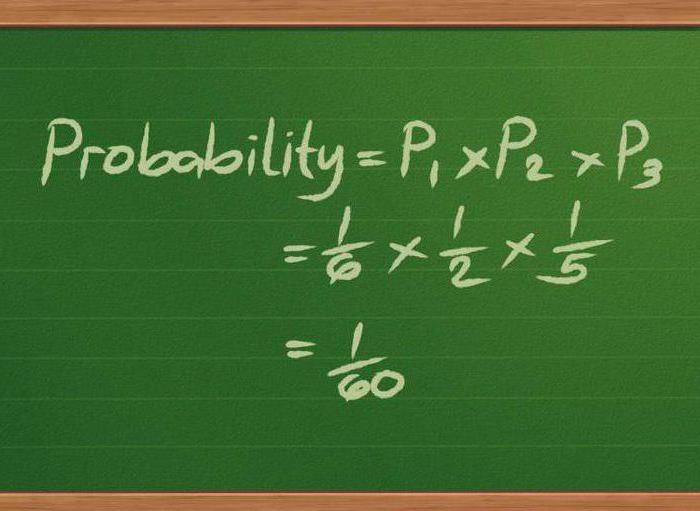
In diesem Abschnitt der Mathematik werden Finanzstrukturen analysiert, die unter unsicheren Bedingungen arbeiten. Es wurde entwickelt, um die rationalsten Methoden für die Verwaltung von finanziellen Vermögenswerten und Strukturen zu finden, wobei Faktoren wie die stochastische Entwicklung, das Risiko, die Zeit usw. berücksichtigt werden.
In der Wissenschaft ist es üblich, folgende Strukturen und Objekte zu unterscheiden, die in der Finanzmathematik insgesamt verwendet werden:
- Firmen (zum Beispiel Firmen);
- Einzelpersonen;
- Vermittlungsstrukturen (Pensionskassen, Banken);
- Finanzmärkte.
Der Hauptgegenstand des Studiums der stochastischen Finanzmathematik ist genau der letzte. Dieser Abschnitt basiert auf solchen Disziplinen wie Statistik von Zufallsprozessen, Theorie von Zufallsprozessen usw.
Gegenwärtig ist es aus zahlreichen Nachrichten und Veröffentlichungen in den Medien weit entfernt von der Wissenschaft bekannt, dass sich die Werte der sogenannten globalen Finanzindizes (zum Beispiel des Dow Jones-Index) und der Aktienkurse zufällig ändern. L. Bachelier machte den ersten Versuch, die Entwicklung der Aktienkurse mit Hilfe der Mathematik zu beschreiben. Seine stochastische Methode basiert auf der Wahrscheinlichkeitstheorie. Die Dissertation von L. Bachelier, in der dieser Versuch vorgestellt wird, wurde 1900 veröffentlicht. Der Wissenschaftler hat die derzeit als Fair-Value-Formel für Kaufoptionen bekannte Formel bewiesen. Es spiegelt die stochastische Wahrscheinlichkeit wider.
Wichtige Ideen, die später zur Entstehung einer effektiven Markttheorie führten, wurden in der 1953 veröffentlichten Arbeit von M. Kendall vorgestellt. Dieses Papier befasst sich mit der Frage der Aktienkursdynamik. Der Forscher beschreibt es mit stochastischen Prozessen.
Stochastizität in der Physik
Dank an die Physiker E. Fermi, S. Ulam, N. Metropolis und D.Neumann ist eine weit verbreitete Monte-Carlo-Methode. Der Name stammt von einem Casino in der gleichen Stadt in einem Land wie Monaco. Hier lieh sich Onkel Ulam Geld für das Spiel. Die Art der Wiederholung und die Möglichkeit, Prozesse zu studieren, ist vergleichbar mit dem, was in einem Casino geschieht.

Bei Anwendung dieser Modellierungsmethode wird zunächst ein probabilistisches Analogon gesucht. Zuvor wurde die Modellierung in die entgegengesetzte Richtung durchgeführt: Sie wurde verwendet, um das Ergebnis des zuvor erhaltenen deterministischen Problems zu verifizieren. Obwohl ähnliche Ansätze vor der Entdeckung der Monte-Carlo-Methode existierten, waren sie nicht populär und allgemein.
Enrico Fermi verwendete 1930 stochastische Techniken, um die Eigenschaften des gerade entdeckten Neutrons zu berechnen. Monte-Carlo-Methoden wurden später bei der Arbeit am Manhattan-Projekt verwendet, obwohl zu dieser Zeit die Fähigkeiten von Computern erheblich eingeschränkt waren. Aus diesem Grund verbreiteten sie sich erst, als Computer auftauchten.
Stochastische Signale
Reguläre und stochastische Signale haben unterschiedliche Wellenformen. Wenn wir letztere neu messen, erhalten wir Schwingungen, die eine neue Form haben, die sich von der vorherigen unterscheidet, aber eine gewisse Ähnlichkeit in wesentlichen Merkmalen aufweist. Ein Beispiel für ein stochastisches Signal ist die Aufzeichnung von Seewellenschwingungen.
Warum muss man über diese eher ungewöhnlichen Signale sprechen? Tatsache ist, dass automatische Systeme noch häufiger untersucht werden als vorhergesagt.
Stochastizität und künstliche Intelligenz
Programme für stochastische künstliche Intelligenz arbeiten mit probabilistischen Methoden. Als Beispiel seien Algorithmen wie die stochastische Optimierung oder neuronale Netze genannt. Gleiches gilt für simulierte Annealing- und genetische Algorithmen. In all diesen Fällen kann Stochastizität im eigentlichen Problem oder in der Planung unter der Bedingung der Unsicherheit enthalten sein. Die deterministische Umgebung für einen Modellierungsagenten ist einfacher als stochastisch.

Wie wir sehen, wird das für uns interessante Konzept in vielen Bereichen der Wissenschaft verwendet. Wir haben nur die Hauptanwendungsbereiche aufgeführt und charakterisiert. Das Studium all dieser Prozesse ist sehr wichtig und relevant. Aus diesem Grund wird das für uns interessante Konzept wahrscheinlich lange Zeit in der Wissenschaft angewendet.








