Das Signifikanzniveau in der Statistik ist ein wichtiger Indikator für das Maß an Vertrauen in die Genauigkeit und Wahrheit der empfangenen (vorhergesagten) Daten. Das Konzept ist in verschiedenen Bereichen weit verbreitet: von der Durchführung soziologischer Untersuchungen bis zur statistischen Prüfung wissenschaftlicher Hypothesen.

Definition
Das Niveau der statistischen Signifikanz (oder des statistisch signifikanten Ergebnisses) zeigt die Wahrscheinlichkeit eines zufälligen Auftretens der untersuchten Indikatoren. Die allgemeine statistische Signifikanz des Phänomens wird durch den Koeffizienten p-Wert (p-Pegel) ausgedrückt. Bei jedem Experiment oder jeder Beobachtung ist es wahrscheinlich, dass die erhaltenen Daten auf Stichprobenfehler zurückzuführen sind. Dies gilt insbesondere für die Soziologie.
Das heißt, eine Statistik ist statistisch signifikant, deren Wahrscheinlichkeit eines zufälligen Auftretens äußerst gering ist oder zu Extremen tendiert. Extrem wird in diesem Zusammenhang der Grad der Abweichung der Statistik von der Nullhypothese betrachtet (eine Hypothese, die auf Übereinstimmung mit den erhaltenen Probendaten überprüft wird). In der wissenschaftlichen Praxis wird das Signifikanzniveau vor der Datenerfassung gewählt und der Koeffizient beträgt in der Regel 0,05 (5%). Bei Systemen, bei denen genaue Werte äußerst wichtig sind, kann dieser Indikator 0,01 (1%) oder weniger betragen.
Hintergrund
Das Konzept des Signifikanzniveaus wurde 1925 vom britischen Statistiker und Genetiker Ronald Fisher eingeführt, als er eine Methode zum Testen statistischer Hypothesen entwickelte. Bei der Analyse eines Prozesses besteht eine gewisse Wahrscheinlichkeit für bestimmte Phänomene. Schwierigkeiten treten auf, wenn mit kleinen (oder nicht offensichtlichen) prozentualen Wahrscheinlichkeiten gearbeitet wird, die unter das Konzept des "Messfehlers" fallen.
Bei der Arbeit mit Statistiken, die nicht spezifisch genug sind, um sich zu verifizieren, wurden Wissenschaftler mit dem Problem der Nullhypothese konfrontiert, die kleine Mengen „stört“. Fisher schlug vor, solche Systeme zu definieren Wahrscheinlichkeit von Ereignissen 5% (0,05) als praktisches selektives Segment, mit dem Sie die Nullhypothese in den Berechnungen verwerfen können.
Die Einführung eines festen Koeffizienten
1933 empfahlen die Wissenschaftler Jerzy Neumann und Egon Pearson in ihren Arbeiten vorab (vor der Datenerhebung), ein bestimmtes Signifikanzniveau festzulegen. Beispiele für die Anwendung dieser Regeln sind während der Wahl deutlich sichtbar. Angenommen, es gibt zwei Kandidaten, von denen einer sehr beliebt ist und der zweite wenig bekannt ist. Offensichtlich gewinnt der erste Kandidat die Wahl und die Chancen des zweiten Kandidaten gehen gegen Null. Sie streben - aber nicht gleich: Es gibt immer die Wahrscheinlichkeit höherer Gewalt, sensationelle Informationen und unerwartete Entscheidungen, die das vorhergesagte Wahlergebnis verändern können.
Neumann und Pearson waren sich einig, dass das von Fisher vorgeschlagene Signifikanzniveau von 0,05 (bezeichnet mit dem Symbol α) am bequemsten ist. Fisher selbst wandte sich jedoch 1956 gegen die Festlegung dieses Wertes. Er war der Ansicht, dass der Wert von α unter bestimmten Umständen festgelegt werden sollte. In der Teilchenphysik beträgt sie beispielsweise 0,01.
P-Wert
Der Begriff p-Wert wurde erstmals 1960 in Brownleys Arbeiten verwendet. P-Level (p-Wert) ist ein Indikator, der in umgekehrter Beziehung zur Wahrheit der Ergebnisse steht. Der höchste Koeffizient p-Wert entspricht dem niedrigsten Vertrauensniveau in die Stichprobe der Abhängigkeit zwischen den Variablen.
Dieser Wert gibt die Wahrscheinlichkeit von Fehlern an, die mit der Interpretation der Ergebnisse verbunden sind. Angenommen, p-Pegel = 0,05 (1/20). Es zeigt die Wahrscheinlichkeit von fünf Prozent, dass die Beziehung zwischen den in der Stichprobe gefundenen Variablen nur ein zufälliges Merkmal der Stichprobe ist.Das heißt, wenn diese Abhängigkeit fehlt, kann man bei wiederholten derartigen Experimenten durchschnittlich in jeder zwanzigsten Studie dieselbe oder eine größere Abhängigkeit zwischen den Variablen erwarten. Oft wird der p-Pegel als "akzeptabler Spielraum" des Fehlerpegels angesehen.
Übrigens spiegelt der p-Wert möglicherweise nicht die reale Beziehung zwischen den Variablen wider, sondern zeigt nur einen bestimmten Durchschnittswert innerhalb der Annahmen. Insbesondere hängt die endgültige Analyse der Daten auch von den ausgewählten Werten dieses Koeffizienten ab. Mit einem p-Pegel von 0,05 werden einige Ergebnisse erzielt, mit einem Koeffizienten von 0,01 andere.
Testen statistischer Hypothesen
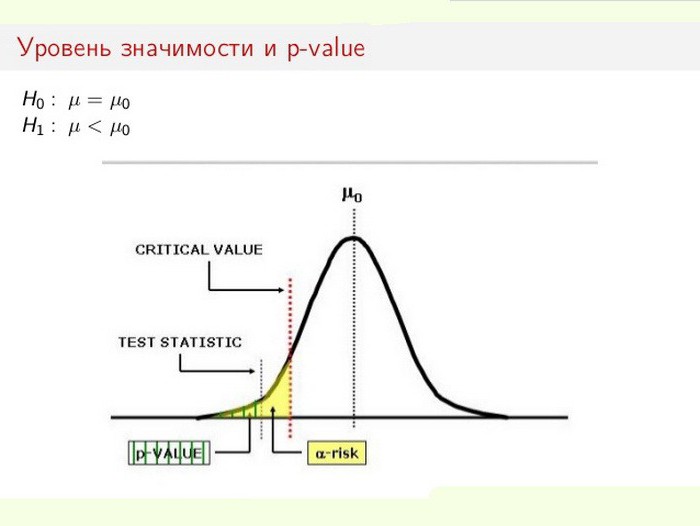
Das Niveau der statistischen Signifikanz ist besonders wichtig beim Testen von Hypothesen. Wenn Sie beispielsweise einen zweiseitigen Test berechnen, wird der Ablehnungsbereich an beiden Enden der Probenverteilung (relativ zur Nullkoordinate) gleichmäßig aufgeteilt und die Richtigkeit der Daten berechnet.
Angenommen, bei der Überwachung eines bestimmten Prozesses (Phänomens) hat sich herausgestellt, dass die neuen statistischen Informationen geringfügige Änderungen gegenüber früheren Werten anzeigen. Darüber hinaus sind die Diskrepanzen in den Ergebnissen gering, nicht offensichtlich, aber wichtig für die Studie. Das Dilemma stellt sich vor dem Fachmann: finden tatsächlich Änderungen statt oder handelt es sich um Stichprobenfehler (fehlerhafte Messungen)?
In diesem Fall wird die Nullhypothese verwendet oder verworfen (alle werden auf einen Fehler zurückgeführt oder die Änderung im System wird als vollendete Tatsache erkannt). Der Prozess zur Lösung des Problems basiert auf dem Verhältnis der statistischen Gesamtsignifikanz (p-Wert) und des Signifikanzniveaus (α). Wenn der p-Pegel <α ist, wird die Nullhypothese verworfen. Je kleiner der p-Wert ist, desto signifikanter ist die Teststatistik.
Verwendete Werte
Das Signifikanzniveau hängt vom zu analysierenden Material ab. In der Praxis werden folgende feste Werte verwendet:
- α = 0,1 (oder 10%);
- α = 0,05 (oder 5%);
- α = 0,01 (oder 1%);
- α = 0,001 (oder 0,1%).
Je genauer die Berechnungen sind, desto niedriger wird der Koeffizient α verwendet. Natürlich erfordern statistische Vorhersagen in Physik, Chemie, Pharma und Genetik eine größere Genauigkeit als in der Politikwissenschaft und Soziologie.

Relevante Schwellenwerte in bestimmten Bereichen
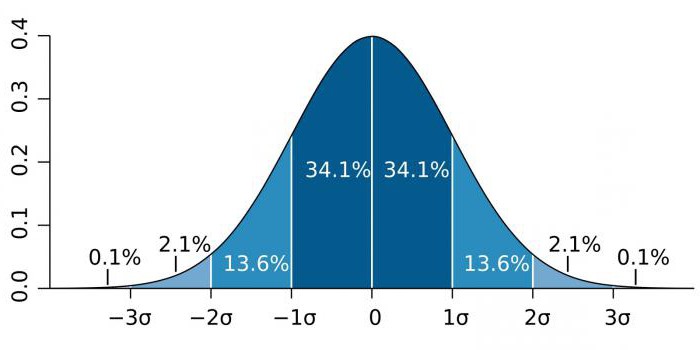
In hochpräzisen Bereichen wie der Teilchenphysik und Fertigungsaktivitäten wird die statistische Signifikanz häufig als Verhältnis der Standardabweichung (angegeben durch den Sigma-Koeffizienten - σ) zur normalen Wahrscheinlichkeitsverteilung (Gauß-Verteilung) ausgedrückt. σ ist ein statistischer Indikator, der die Streuung von Werten eines bestimmten Wertes relativ zu mathematischen Erwartungen bestimmt. Wird verwendet, um die Wahrscheinlichkeit von Ereignissen zu zeichnen.
Je nach Wissensgebiet variiert der Koeffizient σ stark. Wenn zum Beispiel das Vorhandensein des Higgs-Bosons vorhergesagt wird, beträgt der Parameter σ fünf (σ = 5), was dem Wert p-value = 1 / 3,5 Mio. entspricht. In Untersuchungen von Genomen kann das Signifikanzniveau 5 × 10 betragen-8Das ist in diesem Bereich keine Seltenheit.
Wirksamkeit
Beachten Sie, dass die Koeffizienten α und p keine genauen Eigenschaften sind. Unabhängig vom Signifikanzniveau in der Statistik des untersuchten Phänomens ist dies keine unbedingte Grundlage für die Annahme der Hypothese. Je kleiner beispielsweise der Wert von α ist, desto größer ist die Wahrscheinlichkeit, dass die festgelegte Hypothese signifikant ist. Es besteht jedoch ein Fehlerrisiko, das die statistische Aussagekraft (Signifikanz) der Studie verringert.
Forscher, die sich ausschließlich auf statistisch signifikante Ergebnisse konzentrieren, können falsche Schlussfolgerungen ziehen. Gleichzeitig ist es schwierig, ihre Arbeit zu überprüfen, da sie Annahmen verwenden (die tatsächlich die Werte von α und p sind). Es wird daher immer empfohlen, neben der Berechnung der statistischen Signifikanz einen weiteren Indikator zu bestimmen - die Größe des statistischen Effekts. Die Stärke eines Effekts ist ein quantitatives Maß für die Stärke eines Effekts.
