Korelační regresní analýza - Toto je jedna z nejčastějších metod studia vztahu mezi numerickými hodnotami. Jeho hlavním cílem je najít vztah mezi těmito dvěma parametry a jeho stupněm s následným odvozením rovnice. Máme například studenty, kteří složili zkoušku z matematiky a angličtiny. Můžeme použít korelaci k určení, zda úspěch jednoho testu ovlivní výsledky u jiného subjektu. Pokud jde o regresní analýzu, pomáhá předpovídat matematické známky na základě bodů získaných v anglické zkoušce a naopak.

Co je graf korelace?
Jakákoli analýza začíná sběrem informací. Čím více to je, tím přesnější je výsledek dosažený na konci. Ve výše uvedeném příkladu máme dvě disciplíny, ve kterých musí studenti složit zkoušku. Jejich úspěšnost je odhad. Korelační-regresní analýza ukazuje, zda výsledek jednoho subjektu ovlivňuje body získané ve druhé zkoušce. Pro zodpovězení této otázky je nutné analyzovat hodnocení všech studentů současně. Nejprve se ale musíte rozhodnout o závislé proměnné. V tomto případě to není tak důležité. Předpokládejme, že matematická zkouška proběhla dříve. Body na něm jsou nezávislou proměnnou (jsou odloženy podél úsečky). Angličtina je na plánu později. Odhady založené na ní jsou tedy závislou proměnnou (jsou vyneseny podél ordinátu). Čím více takto získaný graf vypadá jako přímka, tím silnější je lineární korelace mezi dvěma vybranými hodnotami. To znamená, že studenti matematiky mají větší šanci získat pětky v anglické zkoušce.
Předpoklady a zjednodušení
Metoda korelační a regresní analýzy zahrnuje nalezení příčinného vztahu. V první fázi však musíte pochopit, že změny v obou množstvích mohou být způsobeny asi třetinou, které výzkumník dosud nezohlednil. Rovněž mohou existovat nelineární vztahy mezi proměnnými, proto získání koeficientu rovného nule není konec experimentu.
Pearsonova lineární korelace
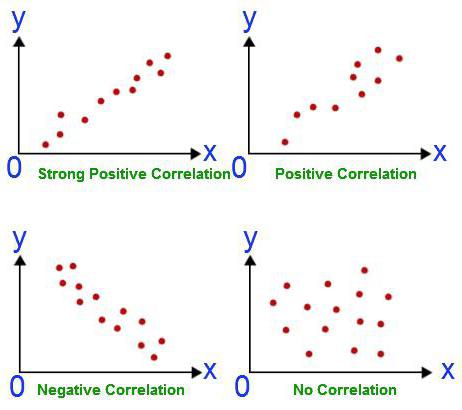
Tento koeficient lze použít za dvou podmínek. První - všechny hodnoty proměnných jsou racionální čísla, druhé - očekává se, že hodnoty se úměrně mění. Tento koeficient je vždy mezi -1 a 1. Pokud je větší než nula, pak existuje přímo úměrná závislost, méně - inverzně, stejná - tyto hodnoty se nijak neovlivňují. Schopnost vypočítat tento ukazatel je základem korelační a regresní analýzy. Poprvé byl tento koeficient vyvinut Karlem Pearsonem na základě myšlenky Františka Galtona.
Vlastnosti a upozornění
Pearsonův korelační koeficient je mocným nástrojem, ale měl by být také používán s opatrností. Používají se následující varování:
- Pearsonův koeficient označuje přítomnost nebo nepřítomnost lineárního vztahu. Korelační-regresní analýza tam nekončí, může se ukázat, že proměnné jsou přesto vzájemně propojeny.
- Při interpretaci hodnoty koeficientu je třeba dávat pozor. Korelaci lze nalézt mezi velikostí nohy a úrovní IQ.To však neznamená, že jeden indikátor určuje jiný.
- Pearsonův koeficient neříká nic o příčinném vztahu mezi indikátory.

Spearmanův korelační koeficient
Pokud změna hodnoty jednoho indikátoru vede ke zvýšení nebo snížení hodnoty jiného indikátoru, pak to znamená, že spolu souvisí. Korelační-regresní analýza, jejíž příklad bude uveden níže, je s těmito parametry přesně spojena. Koeficient pořadí vám umožňuje zjednodušit výpočty.
Korelační a regresní analýza: příklad
Předpokládejme, že existuje hodnocení účinnosti deseti podniků. Máme dva soudce, kteří jim dávají body. Korelační a regresní analýzu podniku nelze v tomto případě provést na základě lineárního Pearsonova koeficientu. Nezajímá nás vztah mezi hodnoceními rozhodčích. Řady podniků podle soudců jsou důležité.
Tento typ analýzy má následující výhody:
- Neparametrická forma vztahů mezi studovanými veličinami.
- Snadné použití, protože řady lze přiřadit vzestupně i sestupně.
Jediným požadavkem tohoto typu analýzy je potřeba převést zdrojová data.
Problémy s aplikací
Korelační a regresní analýza je založena na následujících předpokladech:
- Pozorování jsou považována za nezávislá (pětinásobná ztráta „orla“ nemá vliv na výsledek dalšího převracení mincí).
- V korelační analýze jsou obě proměnné považovány za náhodné. V regresi - pouze jeden (závislý).
- Při testování hypotézy musí být dodrženo normální rozdělení. Změna závislé proměnné by měla být stejná pro každou hodnotu na ose x.
- Korelační diagram je pouze prvním testem hypotézy o vztahu mezi dvěma řadami parametrů, a nikoli konečným výsledkem analýzy.
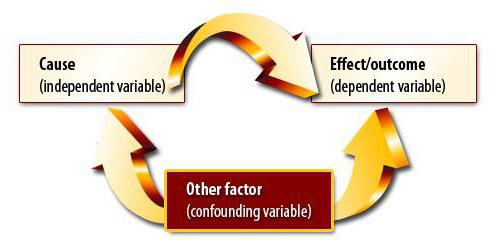
Závislost a příčinná souvislost
Předpokládejme, že jsme vypočítali korelační koeficient objemu vývozu a HDP. Ukázalo se, že se rovná jednotě modulo. Provedli jsme korelační a regresní analýzu až do konce? Samozřejmě ne. Získaný výsledek vůbec neznamená, že HDP lze vyjádřit exportem. Dosud jsme neprokázali příčinný vztah mezi ukazateli. Korelační-regresní analýza - předpovídání hodnot jedné proměnné na základě druhé. Musíte však pochopit, že na parametr často působí mnoho faktorů. Export určuje HDP, ale nejen to. Existují i další faktory. Zde existuje korelace a kauzální vztah, i když upravený o ostatní složky hrubého domácího produktu.
Jiná situace je mnohem nebezpečnější. Ve Velké Británii byl proveden průzkum, který ukázal, že děti, jejichž rodiče kouří, byli častěji pachateli. Tento závěr je založen na silné korelaci mezi ukazatelem. Ale má pravdu? Zaprvé by závislost mohla být inverzní. Rodiče by mohli začít kouřit kvůli stresu ze skutečnosti, že se jejich děti neustále mění a porušují zákon. Za druhé, oba parametry mohou být způsobeny třetím. Takové rodiny patří do nízkých sociálních tříd, které se vyznačují oběma problémy. Na základě korelace proto nelze dojít k závěru, že existuje příčinný vztah.
Proč používat regresní analýzu?
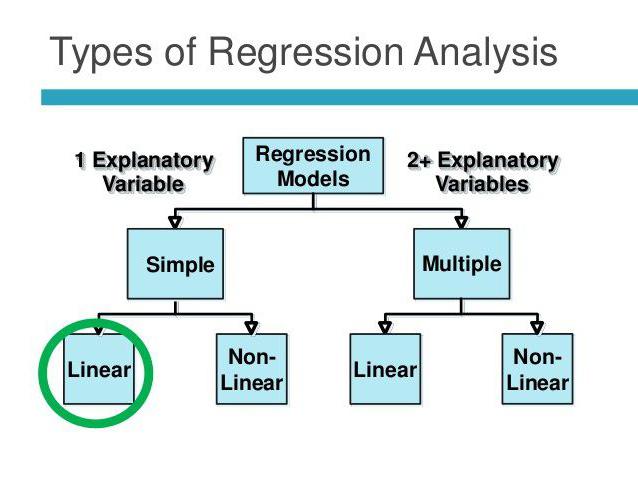
Korelační závislost zahrnuje nalezení vztahů mezi veličinami. Příčinný vztah v tomto případě zůstává za scénami. Úkoly korelační a regresní analýzy se shodují pouze ve smyslu potvrzení existence vztahu mezi hodnotami dvou veličin. Výzkumník však zpočátku nevěnoval pozornost příčinnému vztahu. Regresní analýza má vždy dvě proměnné, z nichž jedna je závislá. Probíhá v několika fázích:
- Výběr správného modelu metodou nejmenších čtverců.
- Odvození rovnice popisující účinek změny nezávislé proměnné na jinou.
Například pokud studujeme vliv věku na lidský růst, pak může regresní analýza pomoci předpovídat změny v průběhu let.
Lineární a vícenásobná regrese
Předpokládejme, že X a Y jsou dvě související proměnné. Regresní analýza nám umožňuje předpovídat velikost jedné z nich na základě hodnot druhé. Například zralost a věk jsou závislé příznaky. Vztah mezi nimi se odráží pomocí lineární regrese. Ve skutečnosti můžete vyjádřit X prostřednictvím Y nebo naopak. Ale často je pouze jedna z regresních linií správná. Úspěch analýzy do značné míry závisí na správném určení nezávislé proměnné. Máme například dva ukazatele: výnos a srážení. Z každodenní zkušenosti je zřejmé, že první závisí na druhém a ne naopak.
Více regresí umožňuje vypočítat neznámou hodnotu na základě hodnot tří nebo více proměnných. Například výnos rýže na akr půdy závisí na kvalitě zrna, úrodnosti půdy, hnojivech, teplotě a srážkách. Všechny tyto parametry ovlivňují celkový výsledek. Pro zjednodušení modelu se používají následující předpoklady:
- Vztah mezi nezávislými a ovlivňujícími charakteristikami je lineární.
- Vyloučena je vícečetnost. To znamená, že závislé proměnné nejsou vzájemně propojeny.
- Homoskedasticita a normalita řady čísel.
Využití korelační a regresní analýzy
Existují tři hlavní případy použití této metody:
- Testování náhodných vztahů mezi veličinami. V tomto případě výzkumník určí hodnoty proměnné a zjistí, zda ovlivňují změnu závislé proměnné. Například můžete lidem dávat různé dávky alkoholu a měřit jejich krevní tlak. V tomto případě vědec ví, že první je příčinou druhého, a ne naopak. Korelační-regresní analýza umožňuje detekovat přímo úměrný lineární vztah mezi těmito dvěma proměnnými a odvodit vzorec, který jej popisuje. V tomto případě lze porovnat hodnoty vyjádřené ve zcela odlišných měrných jednotkách.
- Nalezení vztahu mezi dvěma proměnnými bez rozšíření kauzálního vztahu k nim. V tomto případě není žádný rozdíl v tom, jakou velikost výzkumník volá. Ve skutečnosti se navíc může ukázat, že obě jsou ovlivněny třetí proměnnou, a proto se úměrně mění.
- Výpočet hodnot jedné veličiny na základě druhé. Je založena na rovnici, ve které jsou nahrazena známá čísla.
Korelační analýza tedy zahrnuje nalezení spojení (nikoli příčinné) mezi proměnnými a regresní analýza to vysvětluje, často pomocí matematické funkce.








