Regresní analýza je statistická metoda pro studium závislosti náhodné proměnné na proměnných

Ve statistickém modelování je regresní analýza studie, která se používá k posouzení vztahu mezi proměnnými. Tato matematická metoda zahrnuje mnoho dalších metod pro modelování a analýzu několika proměnných, pokud je kladen důraz na vztah mezi závislou proměnnou a jednou nebo více nezávislými. Přesněji řečeno, regresní analýza pomáhá pochopit, jak se mění typická hodnota závislé proměnné, pokud se změní jedna z nezávislých proměnných, zatímco ostatní nezávislé proměnné zůstávají pevné.

Ve všech případech je cílový odhad funkcí nezávislých proměnných a nazývá se regresní funkce. V regresní analýze je také zajímavé charakterizovat změnu závislé proměnné jako funkci regrese, kterou lze popsat pomocí rozdělení pravděpodobnosti.

Úkoly pro regresní analýzu

Tato statistická metoda výzkumu je široce používána pro předpovídání, kde její použití má významnou výhodu, ale někdy může vést k iluzím nebo falešným vztahům, proto se v této záležitosti doporučuje opatrně ji používat, protože například korelace neznamená příčinný vztah.

Pro provádění regresní analýzy bylo vyvinuto velké množství metod, jako je lineární a obvyklá regrese nejmenších čtverců, které jsou parametrické. Jejich podstatou je, že regresní funkce je definována jako konečný počet neznámých parametrů, které jsou odhadnuty z dat. Neparametrická regrese umožňuje, aby její funkce spočívaly v určité sadě funkcí, které mohou být nekonečné.

Jako metoda statistického výzkumu závisí regresní analýza v praxi na formě procesu generování dat a na tom, jak souvisí s regresním přístupem. Protože skutečná forma datového procesu zpravidla generuje neznámé číslo, regresní analýza dat často do jisté míry závisí na předpokladech o tomto procesu. Tyto předpoklady jsou někdy ověřeny, pokud je k dispozici dostatek dat. Regresní modely jsou často užitečné, i když jsou předpoklady mírně porušeny, ačkoli nemohou pracovat s maximální účinností.

V užším smyslu se regrese může konkrétně týkat posouzení proměnných nepřetržité odezvy, na rozdíl od diskrétních proměnných odezvy použitých při klasifikaci. Případ kontinuální výstupní proměnné se také nazývá metrická regrese, aby se odlišila od souvisejících problémů.

Příběh

Nejčasnější forma regrese je známá metoda nejmenších čtverců. To bylo publikováno Legendre v 1805 a Gauss v 1809. Legendre a Gauss aplikoval metodu k úloze určovat od astronomických pozorování orbity těl kolem slunce (hlavně komety, ale později nově objevené menší planety). Gauss publikoval další vývoj teorie nejmenších čtverců v 1821, včetně verze Gauss-Markov věta.

Termín “regrese” byl vytvořen Francisem Galtonem v 19. století k popisu biologického fenoménu. Pointa byla, že růst potomků z růstu předků se zpravidla ustupuje na normální průměr.Pro Galtona měla regrese pouze tento biologický význam, ale později jeho práce pokračovala Udney Yule a Karl Pearson a přinesla obecnější statistický kontext. V práci Yule a Pearsona je společné rozdělení odpovědí a vysvětlujících proměnných považováno za Gaussovo. Tento předpoklad byl Fisherem odmítnut v pracích z let 1922 a 1925. Fisher navrhl, že podmíněné rozdělení proměnné odezvy je Gaussovo, ale společné rozdělení by nemělo být. V tomto ohledu je Fischerův předpoklad blíže k Gaussově formulaci z roku 1821. Až do roku 1970 trvalo někdy až 24 hodin, než se dostal k výsledku regresní analýzy.

Metody regresní analýzy jsou i nadále oblastí aktivního výzkumu. V posledních desetiletích byly vyvinuty nové metody spolehlivé regrese; regrese zahrnující korelované reakce; regresní metody přizpůsobující různé typy chybějících dat; neparametrická regrese; Bayesovské regresní metody; regrese, ve kterých jsou predikční proměnné měřeny s chybou; regrese s více prediktory než pozorování, jakož i kauzální závěry s regresí.

Regresní modely

Modely regresní analýzy zahrnují následující proměnné:

• Neznámé parametry označené jako beta, což může být skalár nebo vektor.
• Nezávislé proměnné, X.
• Závislé proměnné, Y.

V různých vědních oborech, kde se používá regresní analýza, se místo závislých a nezávislých proměnných používají různé termíny, ale ve všech případech se regresní model týká Y funkcí X a β.

Aproximace má obvykle tvar E (Y | X) = F (X, β). Pro provedení regresní analýzy musí být určen typ funkce f. Méně běžně se zakládá na znalostech vztahu mezi Y a X, které se nespoléhají na data. Pokud takové znalosti nejsou k dispozici, vybere se flexibilní nebo výhodná forma F.

Závislá proměnná Y

Nyní předpokládejme, že vektor neznámých parametrů β má délku k. Pro provedení regresní analýzy musí uživatel poskytnout informace o závislé proměnné Y:

• Pokud existují N datové body tvaru (Y, X), kde N

• Je-li pozorováno přesně N = K a funkce F je lineární, lze rovnici Y = F (X, β) vyřešit přesně a ne přibližně. To se omezuje na řešení řady N-rovnic s N-neznámými (prvky β), které mají jedinečné řešení, pokud je X lineárně nezávislé. Pokud je F nelineární, řešení nemusí existovat nebo může existovat mnoho řešení.
• Nejběžnější je situace, kdy jsou pozorovány N> body k datům. V tomto případě je v datech dostatek informací pro vyhodnocení jedinečné hodnoty pro p, která nejlépe odpovídá datům, a regresní model, když se aplikuje na data, lze v p považovat za overdeterminovaný systém.

V druhém případě poskytuje regresní analýza nástroje pro:

• Nalezení řešení pro neznámé parametry β, které například minimalizuje vzdálenost mezi měřenými a předpovězenými hodnotami Y.
• Za určitých statistických předpokladů používá regresní analýza nadbytečné informace k poskytnutí statistických informací o neznámých parametrech β a predikovaných hodnotách závislé proměnné Y.

Nezbytný počet nezávislých měření

Zvažte regresní model, který má tři neznámé parametry: β₀, β₁ a β₂. Předpokládejme, že experimentátor provádí 10 měření ve stejné hodnotě nezávislé proměnné vektoru X.V tomto případě regresní analýza neposkytuje jedinečnou sadu hodnot. Nejlepší věc, kterou můžete udělat, je vyhodnotit střední a směrodatnou odchylku závislé proměnné Y. Měřením dvou různých hodnot X stejným způsobem můžete získat dostatek dat pro regresi se dvěma neznámými, ale ne pro tři nebo více neznámých.

Pokud byla měření experimentátora provedena na třech různých hodnotách nezávislé proměnné vektoru X, pak regresní analýza poskytne jedinečnou sadu odhadů pro tři neznámé parametry v p.

V případě obecné lineární regrese je výše uvedené tvrzení rovnocenné požadavku, aby matice X^TX je reverzibilní.

Statistické předpoklady

Když je počet měření N větší než počet neznámých parametrů k a chyba měření ε_i, pak je zpravidla přebytek informací obsažených v měřeních distribuován a použit pro statistické předpovědi týkající se neznámých parametrů. Tento nadbytek informací se nazývá stupeň svobody regrese.

Základní předpoklady

Klasické předpoklady pro regresní analýzu zahrnují:

• Vzorek reprezentuje predikci inference.
• Chyba je náhodná proměnná s průměrnou hodnotou nula, což je podmíněno vysvětlujícími proměnnými.
• Nezávislé proměnné se měří bez chyby.
• Jako nezávislé proměnné (prediktory) jsou lineárně nezávislé, to znamená, že není možné vyjádřit žádný prediktor ve formě lineární kombinace ostatních.
• Chyby jsou nekorelované, tj. Kovarianční matice diagonálních chyb a každý nenulový prvek jsou rozptylem chyby.
• Rozptyl chyby je podle pozorování konstantní (homoskedasticita). Pokud ne, můžete použít metodu vážených nejmenších čtverců nebo jiné metody.

Tyto dostatečné podmínky pro odhad nejmenších čtverců mají požadované vlastnosti, zejména tyto předpoklady znamenají, že odhady parametrů budou objektivní, konzistentní a účinné, zejména pokud se vezmou v úvahu ve třídě lineárních odhadů. Je důležité si uvědomit, že důkaz málokdy splňuje podmínky. To znamená, že metoda se používá, i když předpoklady nejsou pravdivé. Variace předpokladů mohou být někdy použity jako měřítko užitečnosti tohoto modelu. Mnoho z těchto předpokladů lze zmírnit pokročilejšími metodami. Statistické analytické zprávy obvykle zahrnují analýzu testů založených na vzorových datech a metodologii užitečnosti modelu.

Kromě toho se proměnné v některých případech vztahují k hodnotám měřeným v bodových bodech. V proměnných, které porušují statistické předpoklady, mohou existovat prostorové trendy a prostorová autokorelace. Geograficky vážená regrese je jedinou metodou, která s těmito údaji pracuje.

Lineární regresní analýza

V lineární regresi je vlastnost závislá proměnná, která je Y_ije lineární kombinace parametrů. Například v jednoduché lineární regresi je pro modelování n-bodů použita jedna nezávislá proměnná x_ia dva parametry, β₀ a β₁.

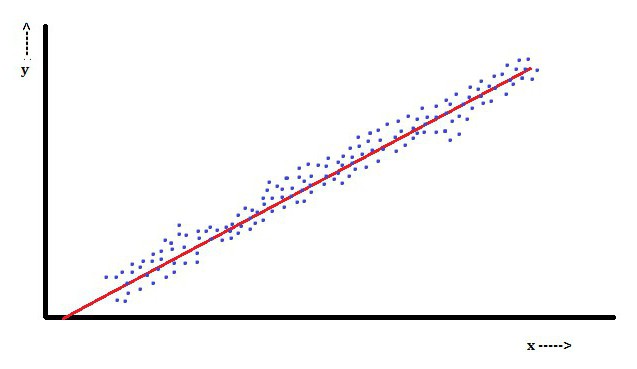
S vícenásobnou lineární regresí existuje několik nezávislých proměnných nebo jejich funkcí.

S náhodným vzorkováním z populace jeho parametry umožňují získat model lineárního regresního modelu.

Z tohoto hlediska je nejoblíbenější metoda nejmenších čtverců. Při jeho použití se získají odhady parametrů, které minimalizují součet zbytkových zbytků na druhou. Tento druh minimalizace (který je charakteristický pro lineární regresi) této funkce vede k sadě normálních rovnic a sadě lineárních rovnic s parametry, které jsou řešeny pro získání odhadů parametrů.

Za dalšího předpokladu, že se chyba populace obvykle šíří, může vědec tyto odhady standardních chyb použít k vytvoření intervalů spolehlivosti a testování hypotéz o jejích parametrech.

Nelineární regresní analýza

Příklad, kdy funkce není s ohledem na parametry lineární, naznačuje, že součet čtverců by měl být minimalizován pomocí iteračního postupu. To představuje mnoho komplikací, které určují rozdíly mezi lineárními a nelineárními metodami nejmenších čtverců. V důsledku toho jsou výsledky regresní analýzy pomocí nelineární metody někdy nepředvídatelné.

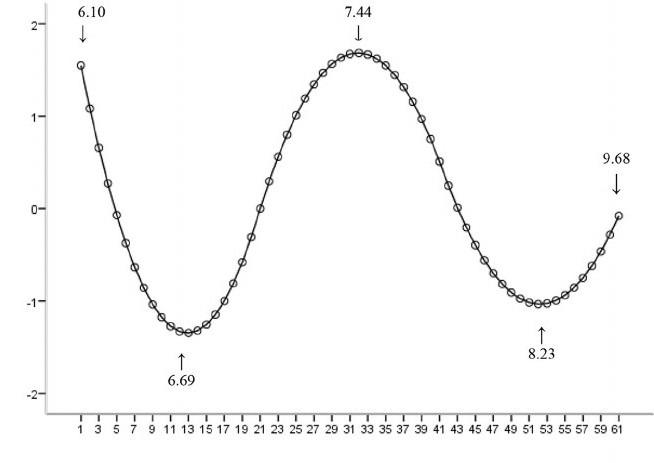
Výpočet výkonu a velikosti vzorku

Zde zpravidla neexistují žádné konzistentní metody týkající se počtu pozorování ve srovnání s počtem nezávislých proměnných v modelu. První pravidlo bylo navrženo Goodem a Hardinem a vypadá jako N = t ^ n, kde N je velikost vzorku, n je počet nezávislých proměnných a t je počet pozorování nezbytných k dosažení požadované přesnosti, pokud model měl pouze jednu nezávislou proměnnou. Například výzkumník vytváří lineární regresní model s použitím datového souboru, který obsahuje 1 000 pacientů (N). Pokud se výzkumný pracovník rozhodne, že pro přesné určení linie (m) je potřeba pět pozorování, pak maximální počet nezávislých proměnných, které model podporuje, jsou 4.

Další metody

Přes skutečnost, že parametry regresního modelu jsou obvykle odhadovány pomocí metody nejmenších čtverců, existují i ​​jiné metody, které se používají mnohem méně často. Jedná se například o následující metody:

• Bayesovské metody (např. Bayesovská metoda lineární regrese).
• Procentní regrese, která se používá v situacích, kdy je snížení procenta chyb považováno za vhodnější.
• Nejmenší absolutní odchylky, které jsou stabilnější v přítomnosti odlehlých hodnot vedoucích k kvantilní regresi.
• Neparametrická regrese, vyžadující velké množství pozorování a výpočtů.
• Vzdálenost učební metriky, která je studována při hledání významné metrické vzdálenosti v daném vstupním prostoru.

Software

Všechny hlavní statistické softwarové balíčky jsou prováděny s použitím regresní analýzy nejmenších čtverců. V některých tabulkových aplikacích a na některých kalkulačkách lze použít jednoduchou lineární regresi a vícenásobnou regresní analýzu. Ačkoli mnoho statistických softwarových balíčků může provádět různé typy neparametrické a spolehlivé regrese, tyto metody jsou méně standardizované; různé softwarové balíčky implementují různé metody. Specializovaný regresní software byl vyvinut pro použití v oblastech, jako je vyšetřovací analýza a neuroimaging.