"Stochastic" je slovo, které fyzici, matematici a další vědci používají k popisu procesů, které mají prvek náhody. Jeho původ je starověký Řek. Přeloženo, znamená to „schopen hádat.“
Význam slova „stochastic“

"Stochastic" je koncept, který se používá v mnoha různých vědních oborech. Znamená to náhodnost, náhodnost, nejistota něčeho. V etice Aristotela (jeho sochařský portrét je uveden výše) je pojem „stochastický“ definice, která odkazuje na schopnost hádat. Matematici to samozřejmě používali na základě toho, že prvek náhody se objevuje právě tehdy, když je to nutné uhodnout. Slovo „stochastické“ je pojem, který je v Novém mezinárodním slovníku definován jako „domněnka“.
Lze tedy poznamenat, že technický význam tohoto pojmu přesně neodpovídá jeho slovnímu (lexikálnímu) významu. Někteří autoři používají výraz „stochastický proces“ jako synonymum pro termín „náhodný proces“.
Stochasticita v matematice

Použití tohoto termínu v matematice je v současné době velmi rozšířené. Například v teorii pravděpodobnosti existuje takový koncept jako stochastický proces. Jeho výsledek nemůže být určen počátečním stavem tohoto systému.
Použití pojmu „stochasticity“ v matematice je přičítáno dílům Vladislava Bortskeviče. Byl to on, kdo použil tento termín ve smyslu „předložených hypotéz“. V matematice, obzvláště v takové části této vědy jako teorie pravděpodobnosti, hraje pole náhodného výzkumu důležitou roli. Existuje například něco jako stochastická matrice. Sloupce nebo řádky této matice se sčítají.
Stochastická matematika (finanční)
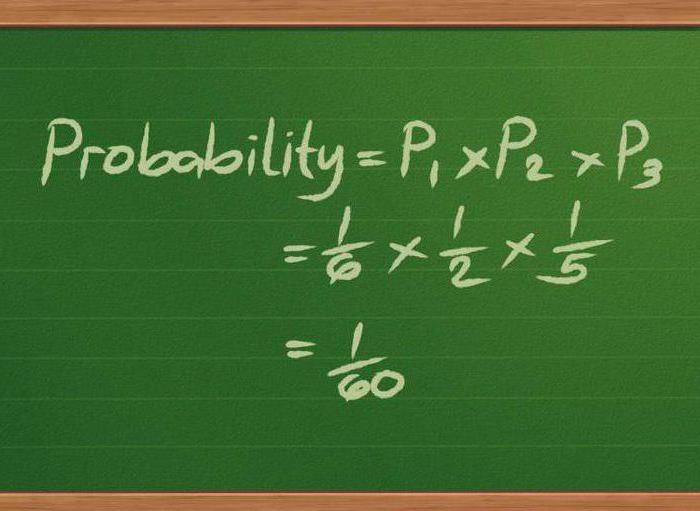
Tato část matematiky analyzuje finanční struktury pracující v podmínkách nejistoty. Je navržen tak, aby nalezl nejracionálnější metody správy finančních aktiv a struktur, s přihlédnutím k faktorům, jako je stochastický vývoj, riziko, čas atd.
Ve vědě je obvyklé rozlišovat následující struktury a objekty, které se používají ve finanční matematice jako celku:
- firmy (například společnosti);
- jednotlivci;
- zprostředkovatelské struktury (penzijní fondy, banky);
- finanční trhy.
Hlavním předmětem studia stochastické finanční matematiky je právě poslední z nich. Tato část je založena na takových disciplínách, jako je statistika náhodných procesů, teorie náhodných procesů atd.
V současné době, dokonce i lidé daleko od vědy, je z četných zpráv a publikací v médiích známo, že hodnoty tzv. Globálních finančních indexů (například index Dow Jones), ceny akcií se mění náhodně. L. Bachelier učinil první pokus popsat pomocí matematiky vývoj cen akcií. Jeho stochastická metoda je založena na teorii pravděpodobnosti. Disertace L. Bacheliera, která tento pokus představuje, byla vydána v roce 1900. Vědec prokázal vzorec, který je v současné době známý jako vzorec reálné hodnoty pro opce na volání. Odráží stochastickou pravděpodobnost.
Důležité myšlenky, které následně vedly ke vzniku efektivní teorie trhu, byly představeny v práci M. Kendalla, publikované v roce 1953. Tento článek se zabývá otázkou dynamiky cen akcií. Výzkumník to popisuje pomocí stochastických procesů.
Stochasticita ve fyzice
Díky fyzikům E. Fermi, S. Ulam, N. Metropolis a D.Neumann je široce používaná metoda Monte Carlo. Jeho název pochází z kasina, které se nachází ve stejném městě v zemi, jako je Monako. Právě zde si strýc Ulam půjčil peníze do hry. Použití charakteru opakování a šance na studium procesů je podobné tomu, co se děje v kasinu.

Při použití této modelovací metody je nejprve prohledáván pravděpodobnostní analog. Předtím bylo modelování prováděno v opačném směru: bylo použito k ověření výsledku deterministického problému získaného dříve. Ačkoli podobné přístupy existovaly před objevením metody Monte Carlo, nebyly populární a obecné.
Enrico Fermi v roce 1930 použil stochastické techniky k výpočtu vlastností neutronu, který byl právě objeven v té době. Metody Monte Carlo byly později použity při práci na projektu Manhattan, ačkoli v té době byly možnosti počítačů výrazně omezeny. Z tohoto důvodu se rozšířily až poté, co se objevily počítače.
Stochastické signály
Pravidelné a stochastické signály mají různé průběhy. Pokud to změříme, získáme oscilace, které mají nový tvar, který se liší od předchozího, ale vykazuje určitou podobnost v základních vlastnostech. Příkladem stochastického signálu je záznam kmitů mořských vln.
Proč je nutné mluvit o těchto poněkud neobvyklých signálech? Faktem je, že ve studiu automatických systémů jsou ještě běžnější, než se předpokládalo.
Stochasticita a umělá inteligence
Stochastické programy umělé inteligence pracují pomocí pravděpodobnostních metod. Jako příklad lze uvést algoritmy, jako je stochastická optimalizace nebo neuronové sítě. Totéž platí pro simulované žíhání a genetické algoritmy. Ve všech těchto případech může být stochasticita obsažena v problému jako takovém nebo v plánování něčeho pod podmínkou nejistoty. Deterministické prostředí pro modelovacího agenta je jednodušší než stochastické.

Jak vidíme, pojem zájmu se nám používá v mnoha vědních oborech. Uvádíme a charakterizujeme pouze hlavní oblasti jeho aplikace. Studie všech těchto procesů je, jak vidíte, velmi důležitá a relevantní. Proto je pravděpodobné, že se koncept zájmu, který nás zajímá, bude po dlouhou dobu používat ve vědě.








