Analisi di correlazione e regressione: esempio, attività, applicazione. Metodo di correlazione e analisi di regressione

Analisi di regressione della correlazione - Questo è uno dei metodi più comuni per studiare la relazione tra valori numerici. Il suo obiettivo principale è trovare la relazione tra i due parametri e il suo grado con la successiva derivazione dell'equazione. Ad esempio, abbiamo studenti che hanno superato l'esame di matematica e inglese. Possiamo usare la correlazione per determinare se il successo di un test influisce sui risultati in un altro argomento. Per quanto riguarda l'analisi di regressione, aiuta a prevedere i voti di matematica in base ai punti ottenuti in un esame di inglese e viceversa.

Che cos'è un grafico di correlazione?

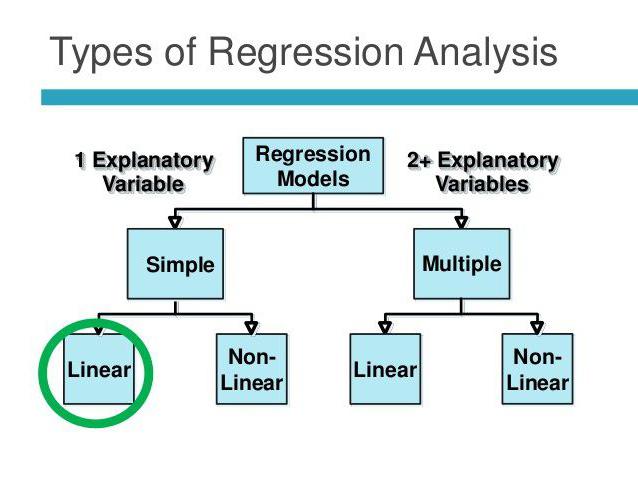
Qualsiasi analisi inizia con la raccolta di informazioni. Più è, più accuratamente il risultato ottenuto alla fine. Nell'esempio sopra, abbiamo due discipline in cui gli studenti devono superare un esame. Il loro tasso di successo è una stima. L'analisi di correlazione-regressione mostra se il risultato di una materia influisce sui punti segnati nel secondo esame. Per rispondere a questa domanda, è necessario analizzare le valutazioni di tutti gli studenti in parallelo. Ma prima devi decidere sulla variabile dipendente. In questo caso, non è così importante. Supponiamo che un esame di matematica abbia avuto luogo prima. I punti su di essa sono una variabile indipendente (sono rinviati lungo l'ascissa). L'inglese è in programma più tardi. Pertanto, le stime basate su di essa sono una variabile dipendente (sono tracciate lungo l'ordinata). Più il grafico così ottenuto appare come una linea retta, più forte è la correlazione lineare tra i due valori selezionati. Ciò significa che gli studenti di matematica hanno maggiori probabilità di ottenere cinque esami d'esame di inglese.

Presupposti e semplificazioni

Il metodo di correlazione e analisi di regressione prevede la ricerca di una relazione causale. Tuttavia, nella prima fase, è necessario comprendere che i cambiamenti in entrambe le quantità possono essere dovuti a un terzo, non ancora preso in considerazione dal ricercatore. Possono esserci anche relazioni non lineari tra le variabili, quindi ottenere un coefficiente uguale a zero non è la fine dell'esperimento.

Correlazione lineare di Pearson

Questo coefficiente può essere utilizzato in base a due condizioni. Il primo - tutti i valori delle variabili sono numeri razionali, il secondo - si prevede che i valori cambino proporzionalmente. Questo coefficiente è sempre tra -1 e 1. Se è maggiore di zero, allora esiste una dipendenza direttamente proporzionale, meno - inversamente, uguale - questi valori non si influenzano a vicenda in alcun modo. La capacità di calcolare questo indicatore è la base dell'analisi di correlazione e regressione. Per la prima volta, questo coefficiente è stato sviluppato da Karl Pearson sulla base dell'idea di Francis Galton.

Proprietà e precauzioni

Il coefficiente di correlazione di Pearson è uno strumento potente, ma dovrebbe anche essere usato con cautela. Sono in uso i seguenti avvisi:

1. Il coefficiente di Pearson indica la presenza o l'assenza di una relazione lineare. L'analisi di correlazione-regressione non termina qui, ma può risultare che le variabili siano comunque interconnesse.
2. Bisogna stare attenti nell'interpretazione del valore del coefficiente. È possibile trovare una correlazione tra dimensione della gamba e livello di QI.Ma ciò non significa che un indicatore ne determini un altro.
3. Il coefficiente di Pearson non dice nulla sulla relazione causale tra gli indicatori.

Coefficiente di correlazione rango di Spearman

Se una variazione del valore di un indicatore determina un aumento o una diminuzione del valore di un altro, ciò significa che sono correlati. L'analisi di correlazione-regressione, di cui verrà fornito un esempio di seguito, è precisamente collegata a tali parametri. Il coefficiente di classificazione consente di semplificare i calcoli.

Analisi di correlazione e regressione: un esempio

Supponiamo che esista una valutazione dell'efficacia di dieci imprese. Abbiamo due giudici che danno loro dei punti. L'analisi di correlazione e regressione dell'impresa in questo caso non può essere effettuata sulla base del coefficiente lineare di Pearson. Non siamo interessati alla relazione tra le valutazioni dei giudici. I ranghi delle imprese secondo i giudici sono importanti.

Questo tipo di analisi presenta i seguenti vantaggi:

• Forma non parametrica delle relazioni tra le quantità studiate.
• Facilità d'uso, perché i gradi possono essere attribuiti sia in ordine crescente di valore che in ordine decrescente.

L'unico requisito di questo tipo di analisi è la necessità di convertire i dati di origine.

Problemi di applicazione

L'analisi di correlazione e regressione si basa sui seguenti presupposti:

• Le osservazioni sono considerate indipendenti (una perdita di cinque volte dell '"aquila" non influisce sul risultato del prossimo lancio della moneta).
• Nell'analisi di correlazione, entrambe le variabili sono considerate casuali. In regressione - solo uno (dipendente).
• Quando si verifica un'ipotesi, è necessario osservare una distribuzione normale. La modifica nella variabile dipendente dovrebbe essere la stessa per ciascun valore sull'ascissa.
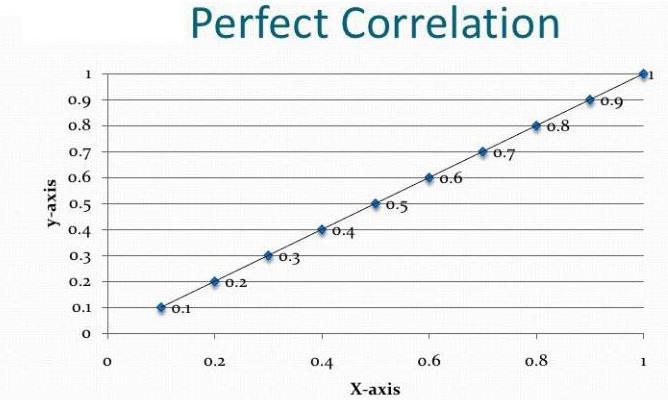
• Il diagramma di correlazione è solo il primo test dell'ipotesi sulla relazione tra le due serie di parametri e non il risultato finale dell'analisi.

Dipendenza e causalità

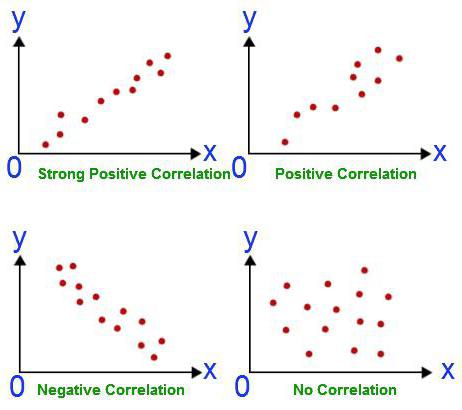
Supponiamo di aver calcolato il coefficiente di correlazione tra volume delle esportazioni e PIL. Si è rivelato essere uguale all'unità modulo. Abbiamo fatto analisi di correlazione e regressione fino alla fine? Certo che no. Il risultato ottenuto non significa affatto che il PIL possa essere espresso attraverso l'esportazione. Non abbiamo ancora dimostrato una relazione causale tra gli indicatori. Analisi di correlazione-regressione: previsione dei valori di una variabile in base a un'altra. Tuttavia, è necessario capire che spesso molti parametri influenzano il parametro. L'esportazione determina il PIL, ma non solo. Ci sono altri fattori Qui c'è una correlazione e una relazione causale, seppure aggiustata per altri componenti del prodotto interno lordo.

Un'altra situazione è molto più pericolosa. Nel Regno Unito, è stato condotto un sondaggio che mostrava che i bambini i cui genitori fumavano erano più spesso autori di reati. Questa conclusione si basa su una forte correlazione tra l'indicatore. Ma ha ragione? Innanzitutto, la dipendenza potrebbe essere inversa. I genitori potrebbero iniziare a fumare a causa dello stress dovuto al fatto che i loro figli subiscono costantemente alterazioni e infrangono la legge. In secondo luogo, entrambi i parametri potrebbero essere dovuti al terzo. Tali famiglie appartengono a classi sociali basse, che sono caratterizzate da entrambi i problemi. Pertanto, in base alla correlazione, non si può concludere che esiste una relazione causale.

Perché usare l'analisi di regressione?

La correlazione dipende dalla ricerca di relazioni tra quantità. La relazione causale in questo caso rimane dietro le quinte. I compiti di correlazione e analisi di regressione coincidono solo in termini di conferma dell'esistenza di una relazione tra i valori di due quantità. Tuttavia, inizialmente il ricercatore non presta attenzione alla possibilità di una relazione causale. L'analisi di regressione ha sempre due variabili, una delle quali dipende. Si svolge in più fasi:

1. Scegliere il modello giusto usando il metodo dei minimi quadrati.
2. Derivazione di un'equazione che descrive l'effetto di una variazione di una variabile indipendente su un'altra.

Ad esempio, se studiamo l'effetto dell'età sulla crescita umana, un'analisi di regressione può aiutare a prevedere i cambiamenti nel corso degli anni.

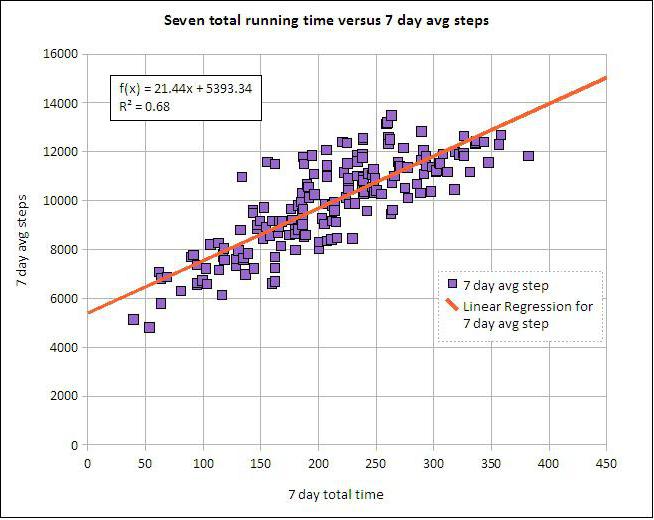
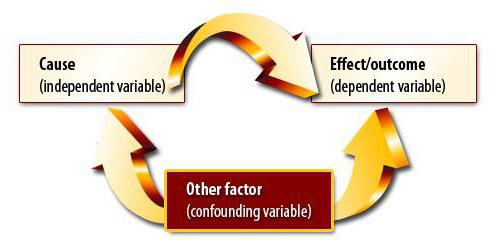
Regressione lineare e multipla

Supponiamo che X e Y siano due variabili correlate. L'analisi di regressione ci consente di prevedere l'entità di uno di essi in base ai valori dell'altro. Ad esempio, la maturità e l'età sono sintomi dipendenti. La relazione tra loro si riflette usando la regressione lineare. In effetti, puoi esprimere da X a Y o viceversa. Ma spesso solo una delle linee di regressione è corretta. Il successo dell'analisi dipende in gran parte dalla corretta determinazione della variabile indipendente. Ad esempio, abbiamo due indicatori: resa e precipitazioni. Dall'esperienza quotidiana, diventa chiaro che il primo dipende dal secondo, e non viceversa.

La regressione multipla consente di calcolare un valore sconosciuto in base ai valori di tre o più variabili. Ad esempio, la resa del riso per acro di terra dipende dalla qualità del grano, dalla fertilità del suolo, dai fertilizzanti, dalla temperatura e dalle precipitazioni. Tutti questi parametri influenzano il risultato complessivo. Per semplificare il modello, vengono utilizzate le seguenti ipotesi:

• La relazione tra caratteristiche indipendenti e influenti è lineare.
• La multicinearità è esclusa. Ciò significa che le variabili dipendenti non sono interconnesse.
• Homoskedasticity e normalità di serie di numeri.

L'uso dell'analisi di correlazione e regressione

Esistono tre casi principali di utilizzo di questo metodo:

1. Test di relazioni casuali tra quantità. In questo caso, il ricercatore determina i valori della variabile e scopre se influenzano il cambiamento nella variabile dipendente. Ad esempio, puoi dare alle persone diverse dosi di alcol e misurare la loro pressione sanguigna. In questo caso, il ricercatore sa per certo che la prima è la causa della seconda, e non viceversa. L'analisi di correlazione-regressione consente di rilevare una relazione lineare direttamente proporzionale tra queste due variabili e derivare una formula che la descrive. In questo caso, è possibile confrontare i valori espressi in unità di misura completamente diverse.
2. Trovare una relazione tra due variabili senza estenderne una relazione causale. In questo caso, non vi è alcuna differenza nelle dimensioni che il ricercatore definisce dipendenti. Inoltre, in realtà, può risultare che entrambi siano interessati dalla terza variabile, quindi cambiano in modo proporzionale.
3. Calcolo dei valori di una quantità in base a un'altra. Si basa su un'equazione in cui vengono sostituiti i numeri noti.

Pertanto, l'analisi di correlazione implica la ricerca di una connessione (non causale) tra le variabili e l'analisi di regressione lo spiega, spesso usando una funzione matematica.