L'analisi di regressione è un metodo statistico per studiare la dipendenza di una variabile casuale da variabili

Nella modellistica statistica, l'analisi di regressione è uno studio utilizzato per valutare la relazione tra variabili. Questo metodo matematico include molti altri metodi per modellare e analizzare diverse variabili, quando l'attenzione è focalizzata sulla relazione tra la variabile dipendente e una o più di quelle indipendenti. Più specificamente, l'analisi di regressione aiuta a capire come cambia un valore tipico di una variabile dipendente se una delle variabili indipendenti cambia, mentre le altre variabili indipendenti rimangono fisse.

In tutti i casi, la stima target è una funzione di variabili indipendenti ed è chiamata funzione di regressione. Nell'analisi di regressione, è anche interessante caratterizzare il cambiamento nella variabile dipendente in funzione della regressione, che può essere descritta usando una distribuzione di probabilità.

Attività di analisi di regressione

Questo metodo di ricerca statistica è ampiamente utilizzato per le previsioni, in cui il suo uso presenta un vantaggio significativo, ma a volte può portare a illusioni o false relazioni, pertanto si consiglia di utilizzarlo con attenzione in questo problema, perché, ad esempio, la correlazione non significa una relazione causale.

Sono stati sviluppati numerosi metodi per condurre l'analisi di regressione, come la regressione lineare e ordinaria dei minimi quadrati, che sono parametrici. La loro essenza è che la funzione di regressione è definita in termini di un numero finito di parametri sconosciuti stimati dai dati. La regressione non parametrica consente alle sue funzioni di trovarsi in un determinato insieme di funzioni, che possono essere di dimensione infinita.

Come metodo di ricerca statistica, l'analisi della regressione in pratica dipende dalla forma del processo di generazione dei dati e da come si collega all'approccio di regressione. Poiché la vera forma del processo dei dati sta generando, di regola, un numero sconosciuto, l'analisi di regressione dei dati dipende spesso in una certa misura dalle ipotesi su questo processo. Questi presupposti vengono talvolta verificati se sono disponibili dati sufficienti. I modelli di regressione sono spesso utili anche quando i presupposti sono moderatamente violati, sebbene non possano funzionare alla massima efficienza.

In un senso più stretto, la regressione può riferirsi specificamente alla valutazione delle variabili di risposta continue, in contrasto con le variabili di risposta discrete utilizzate nella classificazione. Il caso di una variabile di output continua è anche chiamato regressione metrica per distinguerla dai problemi correlati.

La storia

La prima forma di regressione è il noto metodo dei minimi quadrati. Fu pubblicato da Legendre nel 1805 e Gauss nel 1809. Legendre e Gauss applicarono il metodo al compito di determinare dalle osservazioni astronomiche le orbite dei corpi attorno al Sole (principalmente comete, ma in seguito scoperti pianeti minori). Gauss pubblicò un ulteriore sviluppo della teoria dei minimi quadrati nel 1821, inclusa una versione del teorema di Gauss-Markov.

Il termine "regressione" fu coniato da Francis Galton nel 19 ° secolo per descrivere un fenomeno biologico. La linea di fondo era che la crescita dei discendenti dalla crescita degli antenati, di regola, regredisce fino alla media normale.Per Galton, la regressione aveva solo questo significato biologico, ma in seguito il suo lavoro fu continuato da Udney Yule e Karl Pearson e portato in un contesto statistico più generale. Nel lavoro di Yule e Pearson, la distribuzione congiunta di variabili di risposta e variabili esplicative è considerata gaussiana. Questa ipotesi fu respinta da Fisher nelle opere del 1922 e del 1925. Fisher ha suggerito che la distribuzione condizionale della variabile di risposta è gaussiana, ma la distribuzione congiunta non dovrebbe esserlo. A questo proposito, l'ipotesi di Fischer è più vicina alla formulazione di Gauss del 1821. Fino al 1970, a volte ci volevano fino a 24 ore per ottenere il risultato di un'analisi di regressione.

I metodi di analisi della regressione continuano ad essere un'area di ricerca attiva. Negli ultimi decenni, sono stati sviluppati nuovi metodi per una regressione affidabile; regressione con risposte correlate; metodi di regressione che ospitano vari tipi di dati mancanti; regressione non parametrica; Metodi di regressione bayesiana; regressioni in cui le variabili predittive vengono misurate con un errore; regressioni con più predittori delle osservazioni, nonché inferenze causali con regressione.

Modelli di regressione

I modelli di analisi di regressione includono le seguenti variabili:

• Parametri sconosciuti, indicati come beta, che possono essere uno scalare o un vettore.
• Variabili indipendenti, X.
• Variabili dipendenti, Y.

In vari campi della scienza in cui viene applicata l'analisi di regressione, vengono usati vari termini anziché variabili dipendenti e indipendenti, ma in tutti i casi il modello di regressione mette in relazione Y con le funzioni X e β.

L'approssimazione di solito assume la forma E (Y | X) = F (X, β). Per condurre un'analisi di regressione, è necessario determinare il tipo di funzione f. Meno comunemente, si basa sulla conoscenza della relazione tra Y e X che non si basano sui dati. Se tale conoscenza non è disponibile, viene scelto un modulo F flessibile o conveniente.

Variabile dipendente Y

Supponiamo ora che il vettore di parametri sconosciuti β abbia lunghezza k. Per eseguire un'analisi di regressione, l'utente deve fornire informazioni sulla variabile dipendente Y:

• Se ci sono N punti di dati della forma (Y, X), dove N

• Se si osserva esattamente N = K e la funzione F è lineare, l'equazione Y = F (X, β) può essere risolta esattamente e non approssimativamente. Ciò si riduce alla risoluzione di una serie di equazioni N con incognite N (elementi di β), che ha una soluzione unica purché X sia linearmente indipendente. Se F non è lineare, la soluzione potrebbe non esistere o potrebbero esistere molte soluzioni.
• Il più comune è la situazione in cui si osservano N> punti ai dati. In questo caso, ci sono abbastanza informazioni nei dati per valutare il valore univoco per β che corrisponde meglio ai dati e il modello di regressione, quando applicato ai dati, può essere considerato come un sistema sovradeterminato in β.

In quest'ultimo caso, l'analisi di regressione fornisce strumenti per:

• Trovare soluzioni per parametri sconosciuti β, che, ad esempio, minimizzeranno la distanza tra i valori misurati e previsti di Y.
• In base a determinati presupposti statistici, l'analisi di regressione utilizza informazioni in eccesso per fornire informazioni statistiche su parametri sconosciuti β e sui valori previsti della variabile dipendente Y.

Numero necessario di misurazioni indipendenti

Considera un modello di regressione che ha tre parametri sconosciuti: β₀, β₁ e β₂. Supponiamo che lo sperimentatore esegua 10 misurazioni nello stesso valore della variabile indipendente del vettore X.In questo caso, l'analisi di regressione non fornisce un insieme univoco di valori. La cosa migliore che puoi fare è valutare la media e la deviazione standard della variabile dipendente Y. Misurando due diversi valori X allo stesso modo, puoi ottenere dati sufficienti per una regressione con due incognite, ma non per tre o più incognite.

Se le misurazioni dello sperimentatore sono state eseguite a tre diversi valori della variabile indipendente del vettore X, l'analisi di regressione fornirà un insieme unico di stime per tre parametri sconosciuti in β.

Nel caso della regressione lineare generale, l'istruzione precedente è equivalente al requisito che la matrice X^TX è reversibile.

Presupposti statistici

Quando il numero di misurazioni N è maggiore del numero di parametri sconosciuti k e l'errore di misurazione ε_io, quindi, di norma, l'eccesso di informazioni contenute nelle misurazioni viene quindi distribuito e utilizzato per previsioni statistiche relative a parametri sconosciuti. Questo eccesso di informazioni è chiamato il grado di libertà di regressione.

Ipotesi fondamentali

I presupposti classici per l'analisi di regressione includono:

• Il campione è rappresentativo della previsione di inferenza.
• L'errore è una variabile casuale con un valore medio pari a zero, che è condizionata dalle variabili esplicative.
• Le variabili indipendenti vengono misurate senza errori.
• Come variabili indipendenti (predittori), sono linearmente indipendenti, ovvero non è possibile esprimere alcun predittore sotto forma di una combinazione lineare delle altre.
• Gli errori non sono correlati, ovvero la matrice di covarianza degli errori diagonali e ogni elemento diverso da zero sono la varianza dell'errore.
• La varianza dell'errore è costante secondo le osservazioni (omoschedasticità). In caso contrario, è possibile utilizzare il metodo dei minimi quadrati ponderati o altri metodi.

Queste condizioni sufficienti per la stima dei minimi quadrati possiedono le proprietà richieste, in particolare questi presupposti significano che le stime dei parametri saranno obiettive, coerenti ed efficaci, specialmente se prese in considerazione nella classe delle stime lineari. È importante notare che le prove raramente soddisfano le condizioni. Cioè, il metodo viene utilizzato anche se le ipotesi non sono vere. Una variazione di ipotesi può talvolta essere utilizzata come misura di quanto sia utile questo modello. Molte di queste ipotesi possono essere mitigate con metodi più avanzati. I rapporti di analisi statistica in genere includono l'analisi di test basati su dati di esempio e metodologia per l'utilità del modello.

Inoltre, le variabili in alcuni casi si riferiscono a valori misurati nelle posizioni dei punti. Potrebbero esserci tendenze spaziali e autocorrelazione spaziale in variabili che violano ipotesi statistiche. La regressione geografica ponderata è l'unico metodo che si occupa di tali dati.

Analisi di regressione lineare

Nella regressione lineare, una caratteristica è quella della variabile dipendente, che è Y_ioè una combinazione lineare di parametri. Ad esempio, in una semplice regressione lineare, una variabile indipendente, x, viene utilizzata per modellare n-point_ioe due parametri, β₀ e β₁.

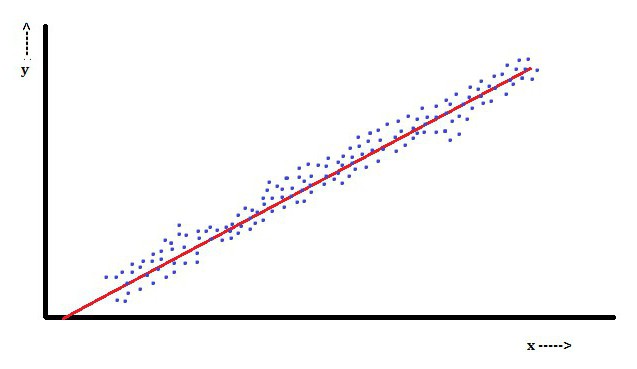
Con la regressione lineare multipla, ci sono diverse variabili indipendenti o le loro funzioni.

Con un campionamento casuale da una popolazione, i suoi parametri consentono di ottenere un esempio di un modello di regressione lineare.

Sotto questo aspetto, il metodo dei minimi quadrati è il più popolare. Usandolo, si ottengono stime dei parametri che minimizzano la somma dei residui quadrati. Questo tipo di minimizzazione (che è caratteristica di una regressione lineare) di questa funzione porta a un insieme di equazioni normali e un insieme di equazioni lineari con parametri che sono risolti per ottenere stime di parametri.

Partendo dal presupposto che un errore della popolazione si diffonde di solito, il ricercatore può utilizzare queste stime di errore standard per creare intervalli di confidenza e testare ipotesi sui suoi parametri.

Analisi di regressione non lineare

Un esempio in cui la funzione non è lineare rispetto ai parametri indica che la somma dei quadrati dovrebbe essere minimizzata usando una procedura iterativa. Questo introduce molte complicazioni che determinano le differenze tra i metodi dei minimi quadrati lineari e non lineari. Di conseguenza, i risultati dell'analisi di regressione utilizzando il metodo non lineare sono talvolta imprevedibili.

Calcolo della potenza e della dimensione del campione

Qui, di regola, non ci sono metodi coerenti per quanto riguarda il numero di osservazioni rispetto al numero di variabili indipendenti nel modello. La prima regola è stata proposta da Good e Hardin e assomiglia a N = t ^ n, dove N è la dimensione del campione, n è il numero di variabili indipendenti e t è il numero di osservazioni necessarie per ottenere l'accuratezza desiderata se il modello avesse una sola variabile indipendente. Ad esempio, un ricercatore crea un modello di regressione lineare utilizzando un set di dati che contiene 1000 pazienti (N). Se il ricercatore decide che sono necessarie cinque osservazioni per determinare con precisione la linea (m), il numero massimo di variabili indipendenti che il modello può supportare è 4.

Altri metodi

Nonostante il fatto che i parametri del modello di regressione vengano generalmente stimati utilizzando il metodo dei minimi quadrati, esistono altri metodi che vengono utilizzati molto meno frequentemente. Ad esempio, questi sono i seguenti metodi:

• Metodi bayesiani (ad es. Metodo di regressione lineare bayesiana).
• Regressione percentuale, utilizzata per situazioni in cui una riduzione degli errori percentuali è considerata più appropriata.
• Le più piccole deviazioni assolute, che è più stabile in presenza di valori anomali che portano alla regressione quantile.
• Regressione non parametrica, che richiede un gran numero di osservazioni e calcoli.
• La distanza della metrica di apprendimento, che viene studiata alla ricerca di una distanza metrica significativa in un determinato spazio di input.

software

Tutti i principali pacchetti software statistici vengono eseguiti utilizzando l'analisi di regressione dei minimi quadrati. La regressione lineare semplice e l'analisi della regressione multipla possono essere utilizzate in alcune applicazioni di fogli di calcolo, nonché su alcuni calcolatori. Sebbene molti pacchetti software statistici possano eseguire vari tipi di regressione non parametrica e affidabile, questi metodi sono meno standardizzati; diversi pacchetti software implementano metodi diversi. È stato sviluppato un software di regressione specializzato per l'uso in aree come l'analisi dell'esame e la neuroimaging.