Analiza corelației și regresiei: exemplu, sarcini, aplicație. Metoda corelării și analizei de regresie

Analiza de regresie a corelației - Aceasta este una dintre cele mai frecvente metode pentru studierea relației dintre valorile numerice. Scopul său principal este de a găsi relația dintre cei doi parametri și gradul său cu derivarea ulterioară a ecuației. De exemplu, avem studenți care au promovat examenul de matematică și engleză. Putem folosi corelația pentru a determina dacă succesul unui test afectează rezultatele la un alt subiect. În ceea ce privește analiza de regresie, aceasta ajută la prezicerea notelor de matematică pe baza punctelor obținute la un examen de engleză și invers.

Ce este un grafic de corelație?

Orice analiză începe cu colectarea informațiilor. Cu cât este mai mult, cu atât este mai precis rezultatul obținut la final. În exemplul de mai sus, avem două discipline în care elevii trebuie să susțină un examen. Rata de succes a acestora este estimativă. Analiza corelației-regresiei arată dacă rezultatul unui subiect afectează punctele obținute la al doilea examen. Pentru a răspunde la această întrebare, este necesar să analizăm paralel evaluările tuturor elevilor. Dar mai întâi trebuie să decideți asupra variabilei dependente. În acest caz, nu este atât de important. Să presupunem că un examen de matematică a avut loc mai devreme. Punctele de pe ea sunt o variabilă independentă (sunt amânate de-a lungul abscisei). Engleza este programată mai târziu. Prin urmare, estimările bazate pe aceasta sunt o variabilă dependentă (sunt reprezentate de-a lungul ordonatei). Cu cât graficul astfel obținut arată mai mult ca o linie dreaptă, cu atât este mai puternică corelația liniară dintre cele două valori selectate. Aceasta înseamnă că elevii la matematică sunt mai predispuși să primească cincizeci la examenul de engleză.

Ipoteze și simplificări

Metoda corelației și a analizei de regresie implică găsirea unei relații cauzale. Cu toate acestea, în prima etapă, trebuie să înțelegeți că modificările ambelor cantități se pot datora unei treimi, care nu au fost luate în considerare încă de către cercetător. De asemenea, pot exista relații neliniare între variabile, prin urmare, obținerea unui coeficient egal cu zero nu este sfârșitul experimentului.

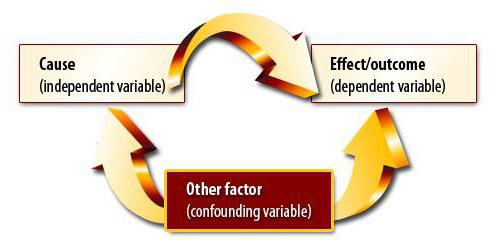
Pearson corelație liniară

Acest coeficient poate fi utilizat sub rezerva a două condiții. Prima - toate valorile variabilelor sunt numere raționale, a doua - este de așteptat ca valorile să se schimbe proporțional. Acest coeficient este întotdeauna între -1 și 1. Dacă este mai mare decât zero, atunci există o dependență direct proporțională, mai puțin - invers, egală - aceste valori nu se afectează în niciun fel. Capacitatea de a calcula acest indicator este baza analizei de corelație și regresie. Pentru prima dată, acest coeficient a fost dezvoltat de Karl Pearson pe baza ideii lui Francis Galton.

Proprietăți și atenționări

Coeficientul de corelație al lui Pearson este un instrument puternic, dar trebuie utilizat și cu prudență. Sunt utilizate următoarele avertismente:

1. Coeficientul Pearson indică prezența sau absența unei relații liniare. Analiza corelației-regresiei nu se încheie aici, se poate dovedi că variabilele sunt totuși interconectate.
2. Trebuie să aveți grijă să interpretați valoarea coeficientului. O corelație poate fi găsită între dimensiunea piciorului și nivelul IQ.Dar acest lucru nu înseamnă că un indicator îl determină pe altul.
3. Coeficientul Pearson nu spune nimic despre relația de cauzalitate dintre indicatori.

Coeficientul de corelație de rang al lui Spearman

Dacă o modificare a valorii unui indicator conduce la o creștere sau o scădere a valorii altuia, atunci aceasta înseamnă că acestea sunt corelate. Analiza corelației-regresiei, dintre care un exemplu va fi prezentat mai jos, este corelată cu asemenea parametri. Coeficientul de rang vă permite să simplificați calculele.

Analiza corelației și regresiei: un exemplu

Să presupunem că există o evaluare a eficienței a zece întreprinderi. Avem doi judecători care le acordă puncte. Analiza de corelație și regresie a întreprinderii în acest caz nu poate fi realizată pe baza coeficientului liniar Pearson. Nu ne interesează relația dintre calificările judecătorilor. Rândurile întreprinderilor în funcție de judecători sunt importante.

Acest tip de analiză prezintă următoarele avantaje:

• Forma nonparametrică a relațiilor dintre cantitățile studiate.
• Ușor de utilizat, deoarece rangurile pot fi atribuite atât în ​​ordine crescătoare a valorii, cât și în ordine descendentă.

Singura cerință a acestui tip de analiză este necesitatea convertirii datelor sursă.

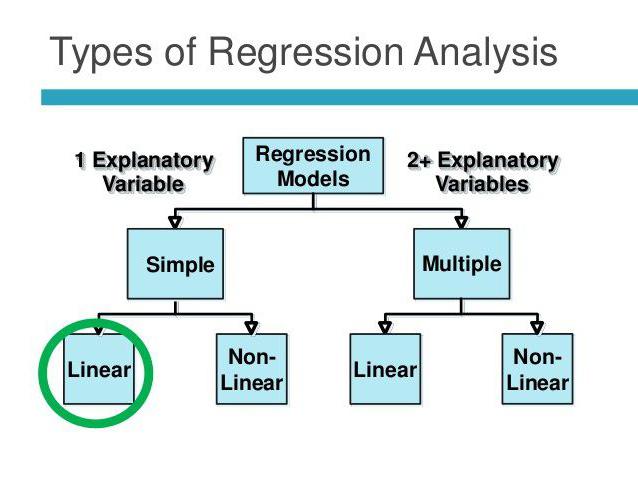
Probleme de aplicare

Analiza de corelație și regresie se bazează pe următoarele ipoteze:

• Observațiile sunt considerate independente (o pierdere de cinci ori a „vulturului” nu afectează rezultatul următoarei flipuri de monedă).
• În analiza corelației, ambele variabile sunt considerate aleatoare. În regresie - doar unul (dependent).
• La testarea unei ipoteze, trebuie respectată o distribuție normală. Modificarea variabilei dependente ar trebui să fie aceeași pentru fiecare valoare de pe abscisă.
• Diagrama de corelație este doar primul test al ipotezei despre relația dintre cele două serii de parametri și nu rezultatul final al analizei.

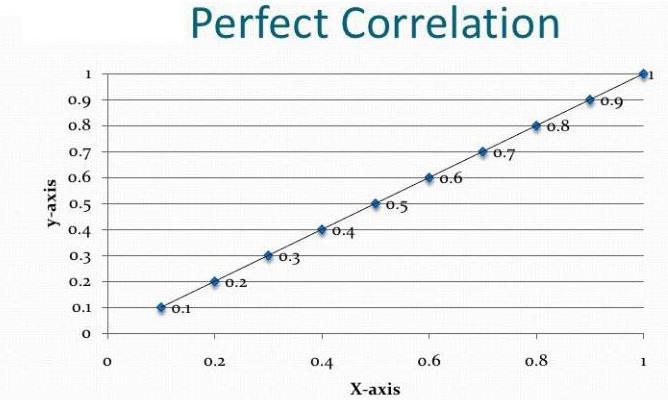
Dependență și cauzalitate

Să presupunem că am calculat coeficientul de corelație al volumului de export și PIB. S-a dovedit a fi egal cu modulul unității. Am făcut o corelație și o analiză de regresie până la sfârșit? Desigur că nu. Rezultatul obținut nu înseamnă deloc că PIB-ul poate fi exprimat prin export. Încă nu am dovedit o relație de cauzalitate între indicatori. Analiza corelației-regresiei - prognozarea valorilor unei variabile bazate pe alta. Cu toate acestea, trebuie să înțelegeți că adesea o mulțime de factori afectează parametrul. Exportul determină PIB-ul, dar nu numai acesta. Există și alți factori. Aici există o corelație și o relație de cauzalitate, deși ajustată pentru alte componente ale produsului intern brut.

O altă situație este mult mai periculoasă. În Marea Britanie, a fost efectuat un sondaj care a arătat că copiii ai căror părinți fumau erau mai des infractori. Această concluzie se bazează pe o corelație puternică între indicator. Dar este corect? În primul rând, dependența ar putea fi inversă. Părinții ar putea începe să fumeze din cauza stresului din cauza faptului că copiii lor intră constant în modificări și încalcă legea. În al doilea rând, ambii parametri se pot datora celui de-al treilea. Astfel de familii aparțin unor clase sociale scăzute, care se caracterizează prin ambele probleme. Prin urmare, pe baza corelației, nu se poate concluziona că există o relație cauzală.

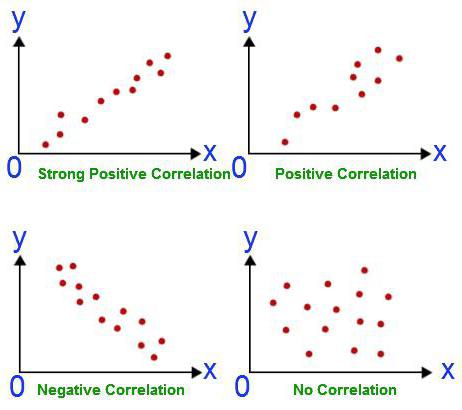
De ce să utilizăm analiza de regresie?

Dependența de corelație presupune găsirea relațiilor între cantități. Relația cauzală în acest caz rămâne în spatele scenei. Sarcinile corelării și analizei de regresie coincid doar în ceea ce privește confirmarea existenței unei relații între valorile a două cantități. Cu toate acestea, inițial cercetătorul nu acordă atenție posibilității unei relații de cauzalitate. Analiza de regresie are întotdeauna două variabile, una dintre ele fiind dependentă. Are loc în mai multe etape:

1. Alegerea modelului potrivit folosind metoda celor mai mici pătrate.
2. Derivarea unei ecuații care descrie efectul unei schimbări într-o variabilă independentă asupra alteia.

De exemplu, dacă studiem efectul vârstei asupra creșterii umane, atunci o analiză de regresie poate ajuta la prezicerea schimbărilor de-a lungul anilor.

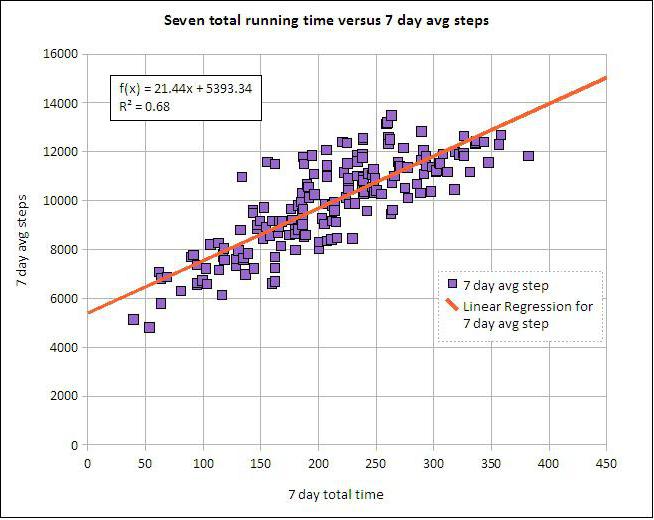
Regresie liniară și multiplă

Să presupunem că X și Y sunt două variabile conexe. Analiza de regresie ne permite să prezicem magnitudinea unuia dintre ei pe baza valorilor celuilalt. De exemplu, maturitatea și vârsta sunt simptome dependente. Relația dintre ele este reflectată folosind regresia liniară. De fapt, puteți exprima X prin Y sau invers. Dar de multe ori doar una dintre liniile de regresie este corectă. Succesul analizei depinde în mare măsură de determinarea corectă a variabilei independente. De exemplu, avem doi indicatori: randamentul și precipitațiile. Din experiența de zi cu zi, devine clar că prima depinde de a doua, și nu invers.

Regresia multiplă vă permite să calculați o valoare necunoscută pe baza valorilor a trei sau mai multe variabile. De exemplu, producția de orez pe acre de teren depinde de calitatea bobului, fertilitatea solului, îngrășăminte, temperatură și precipitații. Toți acești parametri afectează rezultatul general. Pentru a simplifica modelul, se folosesc următoarele ipoteze:

• Relația dintre caracteristicile independente și influențatoare este liniară.
• Multicollinearitatea este exclusă. Aceasta înseamnă că variabilele dependente nu sunt interconectate.
• Homoskedasticitatea și normalitatea seriei de numere.

Utilizarea analizei de corelație și regresie

Există trei cazuri principale de utilizare a acestei metode:

1. Testarea relațiilor casual între cantități. În acest caz, cercetătorul determină valorile variabilei și află dacă acestea afectează modificarea variabilei dependente. De exemplu, puteți oferi oamenilor diferite doze de alcool și măsurați tensiunea arterială. În acest caz, cercetătorul știe cu siguranță că primul este cauza celui de-al doilea, și nu invers. Analiza corelației-regresie vă permite să detectați o relație liniară direct proporțională între aceste două variabile și să derivați o formulă care o descrie. În acest caz, se pot compara valori exprimate în unități de măsură complet diferite.
2. Găsirea unei relații între două variabile fără a extinde o relație cauzală pentru ele. În acest caz, nu există nicio diferență de dimensiunea pe care cercetătorul o numește dependentă. Mai mult, în realitate, se poate dovedi că ambele sunt afectate de a treia variabilă, deci se schimbă proporțional.
3. Calcularea valorilor unei cantități bazată pe alta. Se bazează pe o ecuație în care numerele cunoscute sunt substituite.

Astfel, analiza de corelație implică găsirea unei conexiuni (nu cauzale) între variabile, iar analiza de regresie o explică, folosind adesea o funcție matematică.