L’anàlisi de regressió és un mètode estadístic per estudiar la dependència d’una variable aleatòria de les variables

En la modelització estadística, l’anàlisi de regressió és un estudi utilitzat per avaluar la relació entre variables. Aquest mètode matemàtic inclou molts altres mètodes per modelar i analitzar diverses variables, quan el focus es centra en la relació entre la variable dependent i una o més independents. Més concretament, l’anàlisi de regressió ajuda a entendre com canvia un valor típic d’una variable dependent si una de les variables independents canvia, mentre que les altres variables independents romanen fixes.

En tots els casos, l’estimació objectiu és funció de variables independents i s’anomena funció de regressió. En l'anàlisi de regressió, també és d'interès caracteritzar el canvi de la variable depenent en funció de la regressió, que es pot descriure mitjançant una distribució de probabilitats.

Tasques d’anàlisi de regressió

Aquest mètode d’investigació estadística s’utilitza àmpliament per a la previsió, on el seu ús té un avantatge significatiu, però de vegades pot comportar il·lusions o relacions falses, per tant es recomana utilitzar-lo acuradament en aquest número, perquè, per exemple, la correlació no significa una relació causal.

S'han desenvolupat un gran nombre de mètodes per realitzar anàlisis de regressió, com ara la regressió lineal i ordinària de quadrats mínims, que són paramètriques. La seva essència és que la funció de regressió es defineix en termes d’un nombre finit de paràmetres desconeguts que s’estimen a partir de les dades. La regressió no paramètrica permet a les seves funcions trobar-se en un determinat conjunt de funcions, que poden ser de dimensions infinites.

Com a mètode d’investigació estadística, l’anàlisi de regressió en pràctica depèn de la forma del procés de generació de dades i de com es relaciona amb l’enfocament de regressió. Atès que la forma real del procés de dades està generant, per regla general, un nombre desconegut, l’anàlisi de regressió de les dades sovint depèn en certa mesura dels supòsits sobre aquest procés. De vegades, aquests supòsits es verifiquen si hi ha prou dades disponibles. Els models de regressió solen ser útils, fins i tot quan es vulneren moderadament les hipòtesis, encara que no poden funcionar a la màxima eficiència.

En un sentit més estret, la regressió pot relacionar-se específicament amb l'avaluació de variables de resposta contínua, a diferència de les variables de resposta discret emprades en la classificació. El cas d'una variable de sortida contínua també s'anomena regressió mètrica per distingir-la dels problemes relacionats.

La història

La forma més antiga de regressió és el mètode de menys quadrats conegut. Va ser publicat per Legendre el 1805 i Gauss el 1809. Legendre i Gauss van aplicar el mètode a la tasca de determinar a partir d’observacions astronòmiques les òrbites dels cossos al voltant del Sol (principalment cometes, però després recentment descoberts planetes menors). Gauss va publicar un nou desenvolupament de la teoria dels quadrats mínims el 1821, incloent una versió del teorema de Gauss-Markov.

Francis Galton va inventar el terme "regressió" al segle XIX per descriure un fenomen biològic. El tema de fons va ser que, per regla general, el creixement dels descendents a partir del creixement dels avantpassats es redueix a la mitjana normal.Per a Galton, la regressió només tenia aquest significat biològic, però després la seva tasca fou continuada per Udney Yule i Karl Pearson i portada a un context estadístic més general. En el treball de Yule i Pearson, la distribució conjunta de variables de resposta i variables explicatives es considera gaussiana. Fisher va suposar aquest supòsit en les obres de 1922 i 1925. Fisher va suggerir que la distribució condicional de la variable de resposta és gaussiana, però la distribució conjunta no hauria de ser-ho. En aquest sentit, l’assumpció de Fischer s’acosta més a la formulació de Gauss de 1821. Fins al 1970, de vegades es va trigar fins a 24 hores a obtenir el resultat d’una anàlisi de regressió.

Els mètodes d’anàlisi de regressió continuen sent un àmbit d’investigació activa. En les últimes dècades, s’han desenvolupat nous mètodes per a la regressió fiable; regressió que comporta respostes correlacionades; mètodes de regressió amb diversos tipus de dades que falten; regressió no paramètrica; Mètodes de regressió bayesiana; regressions en què les variables de predicció es mesuren amb un error; regressions amb més predictors que observacions, així com inferències causals amb regressió.

Models de regressió

Els models d’anàlisi de regressió inclouen les següents variables:

• Paràmetres desconeguts, designats com a beta, que poden ser un escalar o un vector.
• Variables independents, X.
• Variables dependents, Y.

En diversos camps de la ciència on s’aplica l’anàlisi de regressió, s’utilitzen diversos termes en lloc de variables dependents i independents, però en tots els casos el model de regressió relaciona Y amb les funcions X i β.

L’aproximació sol tenir la forma E (Y | X) = F (X, β). Per realitzar una anàlisi de regressió, cal determinar el tipus de funció f. Menys comunament, es basa en el coneixement de la relació entre Y i X que no depenen de dades. Si aquest coneixement no està disponible, s'escollirà una forma F flexible o convenient.

Dependent variable Y

Ara suposem que el vector de paràmetres desconeguts β té la longitud k. Per realitzar una anàlisi de regressió, l'usuari ha de proporcionar informació sobre la variable Y dependent:

• Si hi ha N punts de dades del formulari (Y, X), on N

• Si s’observa exactament N = K i la funció F és lineal, l’equació Y = F (X, β) es pot resoldre exactament, i no aproximadament. Això redueix a resoldre un conjunt d'equacions de N amb N-incògnites (elements de β), que té una solució única sempre que X sigui linealment independent. Si F és no lineal, pot ser que la solució no existeixi o que hi hagi moltes solucions.
• El més habitual és la situació en què s’observen N> que apunten a les dades. En aquest cas, hi ha prou informació a les dades per avaluar el valor únic per a β que s’ajusta millor a les dades, i el model de regressió, quan s’aplica a les dades, es pot considerar com un sistema sobredeterminat en β.

En aquest darrer cas, l’anàlisi de regressió proporciona eines per a:

• Trobar solucions per a paràmetres desconeguts β, que, per exemple, minimitzarà la distància entre els valors mesurats i els previstos de Y.
• Sota determinats supòsits estadístics, l'anàlisi de regressió utilitza l'excés d'informació per proporcionar informació estadística sobre els paràmetres β desconeguts i els valors predits de la variable dependent Y.

Nombre necessari de mesures independents

Considereu un model de regressió que tingui tres paràmetres desconeguts: β₀, β₁ i β₂. Suposem que l’experimentador realitza 10 mesures en el mateix valor de la variable independent del vector X.En aquest cas, l’anàlisi de regressió no proporciona un conjunt únic de valors. El millor que podeu fer és avaluar la mitjana i la desviació estàndard de la variable dependent Y. Mesurant dos valors X diferents de la mateixa manera, podeu obtenir prou dades per a una regressió amb dues incògnites, però no per a tres o més incògnites.

Si les mesures de l’experimentador es van dur a terme a tres valors diferents de la variable independent del vector X, l’anàlisi de regressió proporcionarà un conjunt únic d’estimacions per a tres paràmetres desconeguts en β.

En el cas de la regressió lineal general, la sentència anterior equival al requisit que la matriu X^TX és reversible.

Supòsits estadístics

Quan el nombre de mesures N és major que el nombre de paràmetres desconeguts k i l'error de mesura ε_joaleshores, per regla general, l’excés d’informació contingut en les mesures es distribueix i s’utilitza per a previsions estadístiques sobre paràmetres desconeguts. Aquest excés d’informació s’anomena grau de llibertat de regressió.

Supòsits fonamentals

Els supòsits clàssics per a l'anàlisi de regressió inclouen:

• La mostra és representativa de la predicció d’inferència.
• L’error és una variable aleatòria amb un valor mitjà de zero, que depèn de les variables explicatives.
• Les variables independents es mesuren sense error.
• Com a variables independents (predictors), són linealment independents, és a dir, no és possible expressar cap predictor en forma d’una combinació lineal dels altres.
• Els errors no estan correlacionats, és a dir, la matriu de covariància dels errors en diagonal i cada element diferent de zero és la variància de l'error.
• La variació de l'error és constant segons les observacions (homoskedasticitat). Si no, podeu utilitzar el mètode de quadrats mínims ponderats o altres mètodes.

Aquestes condicions suficients per a l'estimació dels menys quadrats posseeixen les propietats requerides, en particular, aquestes suposicions signifiquen que les estimacions dels paràmetres seran objectives, consistents i efectives, especialment quan es tinguin en compte en la classe d'estimació lineal. És important tenir en compte que les proves rarament compleixen les condicions. És a dir, el mètode s’utilitza encara que els supòsits no siguin certs. De vegades es pot fer servir una variació de supòsits com a mesura de la utilitat d’aquest model. Molts d’aquests supòsits es poden pal·liar mitjançant mètodes més avançats. Els informes d’anàlisi estadística normalment inclouen anàlisis de proves basades en dades de mostra i metodologia d’utilitat del model.

A més, en algunes casos, les variables fan referència a valors mesurats en ubicacions puntuals. Pot ser que hi hagi tendències espacials i autocorrelació espacial en variables que violen els supòsits estadístics. La regressió geogràfica ponderada és l’únic mètode que tracta aquestes dades.

Anàlisi de regressió lineal

En regressió lineal, una característica és que la variable dependent, que és Y_joés una combinació lineal de paràmetres. Per exemple, en una regressió lineal simple, s’utilitza una variable independent, x, per modelar n-punts_joi dos paràmetres, β₀ i β₁.

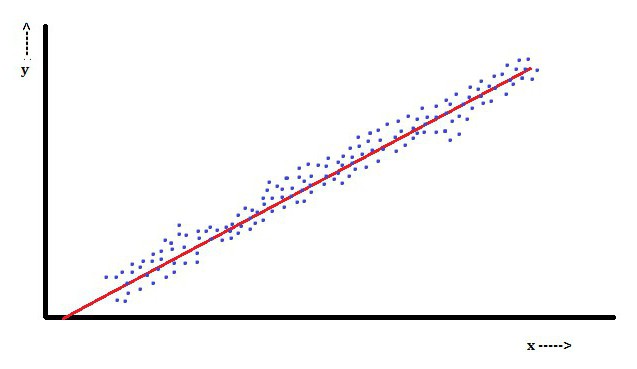
Amb una regressió lineal múltiple, hi ha diverses variables independents o les seves funcions.

Amb el mostreig aleatori d’una població, els seus paràmetres permeten obtenir un model de regressió lineal.

En aquest aspecte, el mètode de menys quadrats és el més popular. Usant-lo, s’obtenen estimacions de paràmetres que minimitzen la suma de residus quadrats. Aquest tipus de minimització (característica d'una regressió lineal) d'aquesta funció condueix a un conjunt d'equacions normals i a un conjunt d'equacions lineals amb paràmetres que es resolen per obtenir estimacions de paràmetres.

Sota el supòsit que normalment es difon l'error de la població, l'investigador pot utilitzar aquestes estimacions d'errors estàndards per crear intervals de confiança i provar hipòtesis sobre els seus paràmetres.

Anàlisi de regressió no lineal

Un exemple en què la funció no és lineal respecte als paràmetres indica que la suma dels quadrats s’ha de minimitzar mitjançant un procediment iteratiu. Això introdueix moltes complicacions que determinen les diferències entre els mètodes de mínims quadrats lineals i no lineals. En conseqüència, els resultats de l'anàlisi de regressió mitjançant el mètode no lineal són a vegades imprevisibles.

Càlcul de potència i mida de la mostra

Aquí, per regla general, no hi ha mètodes coherents quant al nombre d’observacions en comparació amb el nombre de variables independents del model. La primera regla va ser proposada per Good i Hardin i sembla N = t ^ n, on N és la mida de la mostra, n és el nombre de variables independents i t és el nombre d'observacions necessàries per assolir la precisió desitjada si el model tenia una única variable independent. Per exemple, un investigador construeix un model de regressió lineal mitjançant un conjunt de dades que conté 1000 pacients (N). Si l'investigador decideix que es necessiten cinc observacions per determinar amb precisió la línia (m), el nombre màxim de variables independents que pot suportar el model és de 4.

Altres mètodes

Tot i que els paràmetres del model de regressió s’estimen generalment mitjançant el mètode de menys quadrats, hi ha altres mètodes que s’utilitzen amb molta menys freqüència. Per exemple, aquests són els mètodes següents:

• Mètodes bayesians (per exemple, mètode de regressió lineal bayesiana).
• Regressió percentual, que s’utilitza per a situacions en què es considera més adequada una reducció del percentatge d’errors.
• Les desviacions absolutes més petites, que són més estables en presència de valors exteriors que condueixen a una regressió quàntil.
• Regressió no paramètrica, que requereix un gran nombre d’observacions i càlculs.
• La distància de la mètrica d’aprenentatge, que s’estudia a la recerca d’una distància mètrica significativa en un espai d’entrada determinat.

Programari

Tots els principals paquets de programari estadístic es realitzen mitjançant l'anàlisi de regressió dels quadrats mínims. Es poden utilitzar anàlisis de regressió lineal simple i regressió múltiple en algunes aplicacions de fulls de càlcul, així com en algunes calculadores. Tot i que molts paquets de programari estadístic poden realitzar diversos tipus de regressió no paramètrica i fiable, aquests mètodes són menys estandarditzats; diferents paquets de programari implementen mètodes diferents. S'ha desenvolupat un programari de regressió especialitzat per utilitzar-lo en àrees com l'anàlisi d'exàmens i la neuroimatge.