Úroveň významnosti ve statistice je důležitým ukazatelem odrážejícím míru důvěry v přesnost a pravdivost přijatých (předpovězených) údajů. Koncept je široce používán v různých oblastech: od provádění sociologického výzkumu až po statistické testování vědeckých hypotéz.

Definice
Úroveň statistické významnosti (nebo statisticky významného výsledku) ukazuje, jaká je pravděpodobnost náhodného výskytu sledovaných ukazatelů. Obecná statistická významnost jevu je vyjádřena koeficientem p-hodnoty (p-úroveň). Při jakémkoli experimentu nebo pozorování je pravděpodobné, že získaná data jsou způsobena chybami odběru vzorků. To platí zejména pro sociologii.
To znamená, že statistika je statisticky významná, jejíž pravděpodobnost náhodného výskytu je extrémně malá nebo má sklon k extrémům. Za extrémní se v tomto kontextu považuje stupeň odchylky statistik od nulové hypotézy (hypotéza, která je kontrolována z hlediska konzistence se získanými údaji vzorku). Ve vědecké praxi je úroveň významnosti zvolena před sběrem údajů a zpravidla je její koeficient 0,05 (5%). U systémů, kde jsou přesné hodnoty mimořádně důležité, může být tento indikátor 0,01 (1%) nebo nižší.
Pozadí
Koncept úrovně významnosti představil britský statistik a genetik Ronald Fisher v roce 1925, kdy vyvinul metodiku pro testování statistických hypotéz. Při analýze procesu existuje určitá pravděpodobnost určitých jevů. Problémy vznikají při práci s malými (nebo ne zřejmými) procentními pravděpodobnostmi, které spadají pod pojem „chyba měření“.
Při práci se statistikami, které nejsou dostatečně specifické k ověření, se vědci potýkali s problémem nulové hypotézy, která „zasahuje“ do malých množství. Fisher navrhl definovat takové systémy pravděpodobnost událostí 5% (0,05) jako vhodný selektivní řez, který vám umožňuje odmítnout nulovou hypotézu ve výpočtech.
Zavedení pevného koeficientu
V roce 1933 vědci Jerzy Neumann a Egon Pearson ve svých pracích předem (před sběrem údajů) doporučili stanovit určitou úroveň významu. Příklady použití těchto pravidel jsou jasně vidět během voleb. Předpokládejme, že existují dva kandidáti, z nichž jeden je velmi populární a druhý je málo známý. Je zřejmé, že první kandidát vyhraje volby a šance druhého mají sklon k nule. Usilují - ale nejsou si rovni: vždy existuje možnost vyšší moci, senzační informace, neočekávaná rozhodnutí, která mohou změnit předpokládané výsledky voleb.
Neumann a Pearson souhlasili s tím, že Fisherova navrhovaná hladina významnosti 0,05 (označená symbolem a) je nejpohodlnější. Sám Fisher se však v roce 1956 postavil proti fixaci této hodnoty. Věřil, že hladina α by měla být stanovena podle konkrétních okolností. Například ve fyzice částic je to 0,01.
P-hodnota
Termín p-hodnota byl poprvé použit v Brownleyově práci v roce 1960. P-level (p-value) je indikátor, který je nepřímo spojen s pravdivostí výsledků. Nejvyšší hodnota p koeficientu odpovídá nejnižší úrovni spolehlivosti ve vzorku závislosti mezi proměnnými.
Tato hodnota odráží pravděpodobnost chyb spojených s interpretací výsledků. Předpokládejme, že p-úroveň = 0,05 (1/20). Ukazuje pětiprocentní pravděpodobnost, že vztah mezi proměnnými nalezenými ve vzorku je pouze náhodný rys vzorku.To znamená, že pokud tato závislost chybí, lze při opakovaných takových experimentech v průměru v každé dvacáté studii očekávat stejnou nebo větší závislost mezi proměnnými. Úroveň p je často považována za „přijatelný okraj“ úrovně chyb.
Mimochodem, p-hodnota nemusí odrážet skutečný vztah mezi proměnnými, ale pouze ukazuje určitou průměrnou hodnotu v rámci předpokladů. Zejména bude konečná analýza dat také záviset na zvolených hodnotách tohoto koeficientu. Při hladině p = 0,05 budou některé výsledky as koeficientem 0,01 další.
Testování statistických hypotéz
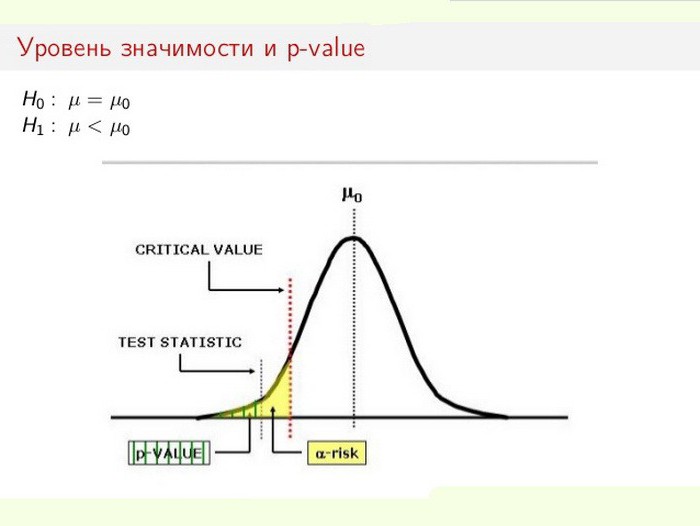
Úroveň statistické významnosti je zvláště důležitá při testování hypotéz. Například při výpočtu oboustranného testu je oblast odmítnutí rozdělena rovnoměrně na oba konce distribuce vzorku (vzhledem k nulové souřadnici) a vypočte se pravda dat.
Předpokládejme, že při monitorování určitého procesu (jevu) se ukázalo, že nové statistické informace naznačují malé změny v porovnání s předchozími hodnotami. Kromě toho jsou rozdíly ve výsledcích malé, nikoli zřejmé, ale důležité pro studii. Dilema vyvstává před odborníkem: dochází ke změnám skutečně nebo k těmto chybám vzorkování (nepřesná měření)?
V tomto případě je použita nebo zamítnuta nulová hypotéza (vše je přičítáno chybě nebo změna v systému je rozpoznána jako hotová věc). Proces řešení problému je založen na poměru celkové statistické významnosti (p-hodnota) a úrovně významnosti (α). Pokud je p-hladina <α, pak je nulová hypotéza odmítnuta. Čím menší je hodnota p, tím významnější je statistika testu.
Použité hodnoty
Úroveň významnosti závisí na analyzovaném materiálu. V praxi se používají následující pevné hodnoty:
- a = 0,1 (nebo 10%);
- a = 0,05 (nebo 5%);
- a = 0,01 (nebo 1%);
- a = 0,001 (nebo 0,1%).
Čím přesnější jsou výpočty, tím nižší je koeficient α. Statistické předpovědi ve fyzice, chemii, farmacii, genetice přirozeně vyžadují větší přesnost než v politické vědě, sociologii.

Hranice relevance v konkrétních oblastech
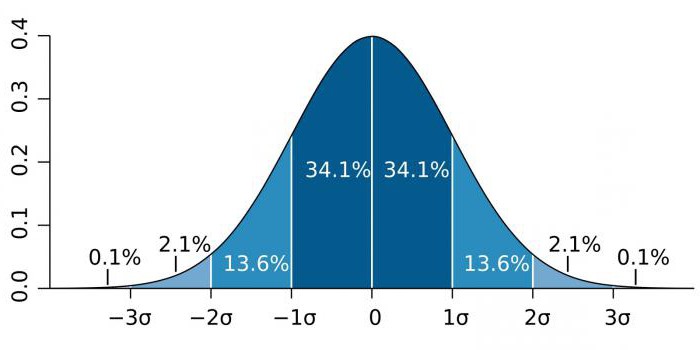
Ve vysoce přesných oblastech, jako je fyzika částic a výrobní činnosti, je statistická významnost často vyjádřena jako poměr standardní odchylky (označený koeficientem sigma - σ) vzhledem k normálnímu rozdělení pravděpodobnosti (Gaussovo rozdělení). σ je statistický ukazatel, který určuje rozptyl hodnot určité hodnoty vzhledem k matematickým očekáváním. Používá se k vykreslení pravděpodobnosti událostí.
V závislosti na poli znalostí se koeficient σ velmi liší. Například při předpovídání existence Higgsova bosonu je parametr σ pět (σ = 5), což odpovídá hodnotě p-hodnota = 1 / 3,5 milionu. Ve studiích genomů může být hladina významnosti 5 × 10-8které nejsou pro tuto oblast neobvyklé.
Účinnost
Mějte na paměti, že koeficienty α a p nejsou přesnými charakteristikami. Ať už je úroveň statistik zkoumaného fenoménu jakákoli, nejedná se o bezpodmínečný základ pro přijetí hypotézy. Například čím menší je hodnota a, tím větší je šance, že zavedená hypotéza je významná. Existuje však riziko chyby, která snižuje statistickou sílu (významnost) studie.
Vědci, kteří se zaměřují výhradně na statisticky významné výsledky, mohou získat chybné závěry. Zároveň je obtížné znovu zkontrolovat jejich práci, protože používají předpoklady (ve skutečnosti jsou to hodnoty α a p-hodnoty). Proto se vždy doporučuje, spolu s výpočtem statistické významnosti, stanovit další ukazatel - velikost statistického efektu. Velikost účinku je kvantitativní míra síly účinku.
