V článku se budeme zabývat konceptem „pravděpodobnosti náhodné události“. Je známo, že v různých oblastech lidské činnosti existují jevy, které nelze přesně předpovědět. Tak například objem prodeje výrobků závisí jak na velmi měnících se potřebách zákazníků, tak na dalších nuancích, které není možné vzít v úvahu. Proto musí vlastníci při vytváření výroby a prodejích předpovídat výsledek své činnosti na základě osobní zkušenosti nebo podobné schopnosti jiných lidí.
Pro vyhodnocení dané události je nutné vzít v úvahu nebo speciálně vytvořit podmínky, za kterých je zaznamenána. Takové akce se nazývají zážitek nebo experiment. V jeho procesu jsou možné epizody, které se nazývají náhodné, pokud se nakonec mohou odehrávat nebo ne, a také spolehlivé jevy, které vznikají v důsledku praxe.
Studujeme pravděpodobnost události pomocí příkladů. Například sněžení v Moskvě 25. listopadu je považováno za náhodnou epizodu. Každodenní svítání je spolehlivý jev a sníh na rovníku sněhu je považován za nemožnou zvědavost. Jedním z nejdůležitějších úkolů v teorii pravděpodobnosti je problém stanovení kvantitativního měřítka možnosti výskytu události.
Pravděpodobnost
Pravděpodobnost je míra (kvantitativní hodnocení, relativní míra) možnosti výskytu události. Když jsou důvody možného výskytu ve skutečnosti vyváženy kontrastními argumenty, je tento případ nazýván pravděpodobný. Jinak se tomu říká pochybné nebo neuvěřitelné.
Převaha negativního základu nad pozitivním a naopak může být v různé míře, kvůli níž je nepřípustnost (nebo přípustnost) menší nebo větší. Z tohoto důvodu je pravděpodobnost události často vnímána na prvotřídní úrovni, zejména v těch pasážích, kde je velmi obtížné nebo nemožné provést přesné kvantitativní hodnocení. Samozřejmě jsou možné různé stupně pravděpodobnosti.
Analýza pravděpodobnosti
Mimochodem, pravděpodobnost nezávislých událostí má zvláštní parametry. A sondování šance z matematické pozice doplňuje specifickou disciplínu - teorii pravděpodobnosti. V této výuce a matematické statistice je pojem přípustnosti oficiálně označen jako číselný popis epizody (pravděpodobnostní míra nebo její význam).
Ve skutečnosti je to míra v mnoha případech (podmnožiny mnoha elementárních jevů), získávání hodnot od 0 do 1:
- hodnota 1 odpovídá platné epizodě;
- nemožná skutečnost má nulovou šanci (konverzace je téměř vždy falešná).
Pokud je výskyt jevu p, pak je riziko inertnosti 1-p. Řekněme, pravděpodobnost ½ znamená stejnou možnost výskytu i neexistence případu.

Pravděpodobnost
Test, událost, pravděpodobnost - tyto proměnné jsou pevně vázány vědou. Typická definice náhody je založena na myšlence rovnoměrnosti výsledků.
Poměr počtu finále přispívajících k této události k celkovému počtu stejně možných zakončení je příležitost. Například přípustnost vypadnutí „ocasu“ nebo „orla“, pokud je neúmyslné házení penny 1/2, je-li vypočítáno, že pouze tyto dvě cesty jsou stejně pravděpodobné.

Tato klasická definice náhody může být zobecněna v případě nevyčerpatelného počtu potenciálních hodnot.Například, pokud se může objevit jakýkoli jev se stejnou přípustností v kterémkoli bodě (počet bodů je neomezený) v některé místní oblasti roviny (prostoru), pak riziko, že se vyskytne v určité části této přijatelné koule, odpovídá poměru plochy (objemu) této části. do oblasti (objemu) oblasti všech možných bodů.
Odkaz
Pravděpodobnost události lze určit empiricky. Je to kvůli frekvenci nástupu epizody založené na skutečnosti, že s působivým počtem testů by frekvence měla sledovat objektivní stupeň možnosti tohoto precedensu.
V současné prezentaci teorie pravděpodobnosti je náhoda odhalena axiomaticky, jako konkrétní skutečnost abstraktní teorie míry souboru. Mezi přípustností vyjadřující stupeň reality výskytu jevu a abstraktním měřítkem je však vazba právě frekvencí jejího sledování.

Pravděpodobnost výskytu události v různých procesech je samozřejmě možná. Stochastická interpretace určitých jevů je široce rozšířena v moderní vědě, zejména v ekonometrii, statistické fyzice termodynamických (viditelných) systémů, kde se ani v případě deterministického klasického popisu pohybu částic nezdá být konkrétní popis jejich celé struktury účelný a prakticky možný. V kvantové fyzice mají charakterizované procesy samy o sobě stochastickou povahu.
Náhodná událost
Pravděpodobnost výskytu události v každém nekontrolovaném procesu je samozřejmě vysoká. Co je to pohotovost? Toto je podmnožina mnoha výsledků náhodného experimentu. Pokud se náhodné vyšetřování mnohokrát opakuje, slouží četnost výskytu skutečnosti jako posouzení její přípustnosti. 
Nedobrovolný jev, k němuž nikdy nedochází v důsledku nedobrovolného experimentu, se nazývá nemožný. Náhodná epizoda, která je vždy realizována jako výsledek neočekávaného experimentu, se nazývá spolehlivá. A jak je charakterizována pravděpodobnost nezávislých událostí? Je známo, že dvě náhodná fakta se nazývají nezávislá, pokud vzhled jednoho z nich nezmění přípustnost vzhledu druhého.
Náhodná událost je pravidelná událost, která je vytvořena generováním nedobrovolných funkcí se substitucí náhodných proměnných do proměnných. Obvyklá funkce generování čísla loterie se provádí pomocí počítačových nástrojů.
Definice
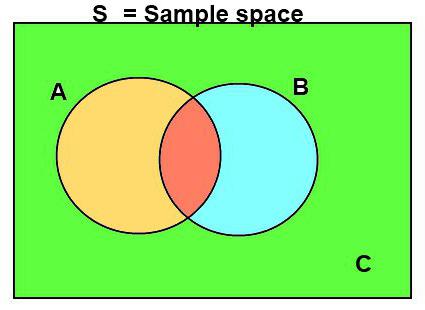
Matematicky náhodná epizoda je podmnožinou prostoru elementárních výsledků nedobrovolné zkoušky. Jedná se o prvek sigma-algebry nebo algebry - F, který je zase nastaven zjevně a společně s prostorem nejjednodušších jevů "Omega" a pravděpodobnost P tvoří pravděpodobnostní prostor.
Souvislosti pojmu náhoda
Pravděpodobnost nehody byla často vyšetřována. Obecně byl vznik pojmu náhoda historicky spojen s hazardními hrami, zejména kostkami. Před vznikem této koncepce byly nastíněny kombinatorické úkoly spočívající v výpočtu počtu potenciálních výsledků při házení dvou kostek, jakož i otázka rozdělení sázek mezi účastníky, když hra skončila před plánem.
Biskup Vibold z města Cambrai v roce 960 rozhodl o prvním rebusu, když hodil tři kostky. Počítal 56 druhů. Toto číslo však ve skutečnosti nereprodukuje součet stejně možných metod, protože každá z jejich 56 verzí může být prováděna odlišným počtem recepcí.
Pravděpodobnost nehody byla studována v první polovině 13. století Richardem de Fornivalem. Navzdory skutečnosti, že také zmiňuje číslo 56, odráží v myšlence, že stejný počet bodů na třech kostech lze získat šesti metodami.
Na základě jeho odůvodnění je již možné prokázat, že počet stejně přístupných možností je 216. Mnoho z nich následně tento problém zcela správně nevyřešilo.Poprvé vypočítal Gallileo Galilei počet stejně přístupných výsledků při házení tří kostí: zvedl šest (počet verzí ztráty jedné kosti) na stupeň 3 (počet kostí). Sestavil také tabulku s počtem možností pro získání různých množství bodů.
Doufáme, že vás náš článek plně seznámil s pravděpodobností náhodné události.








