Korrelációs regressziós elemzés - Ez a leggyakoribb módszer a numerikus értékek közötti kapcsolat tanulmányozására. Legfontosabb célja a két paraméter és annak mértéke közötti kapcsolat megkeresése az egyenlet későbbi származtatásával. Például vannak olyan hallgatók, akik sikeresen teljesítették a matematikai és angol nyelvvizsga tanfolyamot. A korreláció segítségével meghatározhatjuk, hogy az egyik teszt sikere befolyásolja-e a másik alany eredményeit. A regressziós elemzést illetően elősegíti a matematikai osztályzatok előrejelzését az angol vizsga során szerzett pontok alapján, és fordítva.

Mi a korrelációs táblázat?
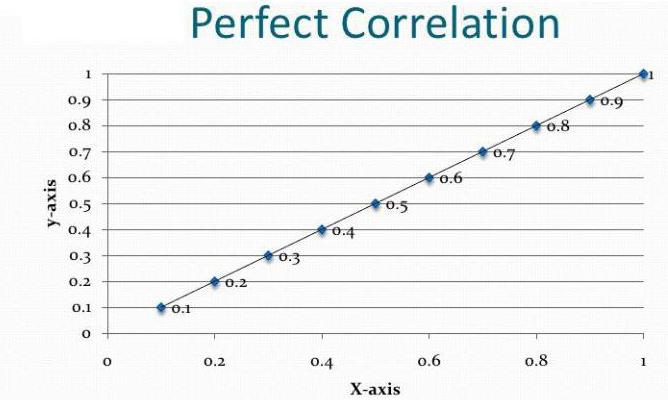
Minden elemzés az információk gyűjtésével kezdődik. Minél több, annál pontosabb a végeredmény. A fenti példában két olyan tudományág van, amelyben a hallgatóknak vizsgát kell teljesíteniük. Sikeres arányuk becsült. A korrelációs-regressziós elemzés azt mutatja, hogy az egyik alany eredménye befolyásolja-e a második vizsga pontszámait. A kérdés megválaszolásához párhuzamosan kell elemezni az összes hallgató értékelését. Először azonban el kell döntenie a függő változóról. Ebben az esetben ez nem olyan fontos. Tegyük fel, hogy a matematikai vizsga korábban zajlott. A rajta lévő pontok egy független változó (ezeket az abszcissza mentén elhalasztják). Az angol nyelv később lesz a menetrendben. Ezért az ezen alapuló becslések függő változó (az ordinátán vannak ábrázolva). Minél inkább az így kapott grafikon egyenes vonalúnak tűnik, annál erősebb a két kiválasztott érték közötti lineáris korreláció. Ez azt jelenti, hogy a matematika hallgatói nagyobb valószínűséggel kapnak ötöst az angol vizsga során.
Feltételek és egyszerűsítések
A korrelációs és regressziós analízis módszere magában foglalja az okozati összefüggés megállapítását. Az első szakaszban azonban meg kell értenie, hogy mindkét mennyiség változása valamilyen harmadik oka lehet, amelyet a kutató még nem vett figyelembe. A változók között nemlineáris összefüggések is lehetnek, ezért a zérus együttható elérése nem a kísérlet vége.
Pearson lineáris korreláció
Ez az együttható két feltétel mellett alkalmazható. Az első - a változók összes értéke racionális szám, a második - várható, hogy az értékek arányosan változnak. Ez az együttható mindig -1 és 1 között van. Ha nagyobb, mint nulla, akkor fennáll egy közvetlenül arányos függőség, kevésbé - fordítva, egyenlő - ezek az értékek semmilyen módon nem befolyásolják egymást. Az indikátor kiszámításának képessége képezi a korreláció és a regressziós elemzés alapját. Ezt az együtthatót először Karl Pearson dolgozta ki Francis Galton ötlete alapján.
Tulajdonságok és figyelmeztetések
A Pearson korrelációs együtthatója erőteljes eszköz, de óvatosan kell alkalmazni. A következő figyelmeztetések vannak használatban:
- A Pearson-együttható egy lineáris kapcsolat meglétét vagy hiányát jelzi. A korrelációs-regressziós elemzés ezzel nem ér véget, kiderülhet, hogy a változók mindazonáltal össze vannak kapcsolva.
- Óvatosan kell értelmezni az együttható értékét. Összefüggést lehet találni a lábméret és az IQ szint között.De ez nem azt jelenti, hogy az egyik mutató meghatározza a másikot.
- A Pearson-együttható nem mond semmit a mutatók közötti okozati összefüggésről.

A Spearman rangkorrelációs együtthatója
Ha az egyik mutató értékének megváltozása egy másik értékének növekedéséhez vagy csökkenéséhez vezet, akkor ez azt jelenti, hogy ezek kapcsolatban állnak. A korrelációs-regressziós elemzés, amelynek példáját az alábbiakban mutatjuk be, pontosan kapcsolódik ezekhez a paraméterekhez. A rangsorolási együttható lehetővé teszi a számítások egyszerűsítését.
Korrelációs és regressziós elemzés: példa
Tegyük fel, hogy felmérjük a tíz vállalkozás hatékonyságát. Két bírónk ad pontokat. A vállalkozás korrelációs és regressziós elemzését ebben az esetben nem lehet lineáris Pearson-együttható alapján elvégezni. Nem érdekli a bírák értékelése közötti kapcsolat. A vállalkozások sora a bírók szerint fontos.
Az ilyen típusú elemzésnek a következő előnyei vannak:
- A vizsgált mennyiségek közötti paraméterek nélküli kapcsolat.
- Könnyű használat, mivel a rangsorokat növekvő értékrendben és csökkenő sorrendben lehet besorolni.
Az ilyen típusú elemzés egyetlen követelménye a forrás adatok konvertálása.
Alkalmazási problémák
A korrelációs és regressziós elemzés a következő feltételezéseken alapszik:
- A megfigyeléseket függetlennek tekintik (a „sas” ötszörös elvesztése nem befolyásolja a következő érme megfordulásának eredményét).
- A korrelációs elemzés során mindkét változó véletlenszerűnek tekinthető. Regresszióban - csak egy (függő).
- A hipotézis tesztelésekor be kell tartani a normál eloszlást. A függő változó változásának azonosnak kell lennie az abszcissza minden egyes értékén.
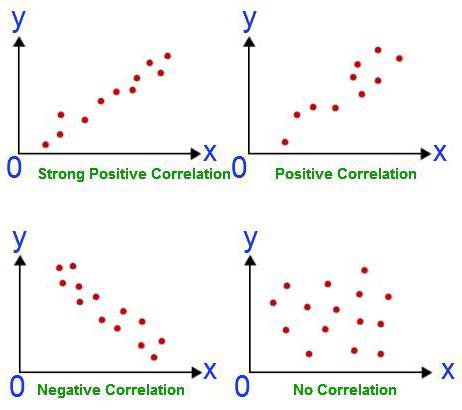
- A korrelációs diagram csak a két paraméter sorozat közötti kapcsolatra vonatkozó hipotézis első tesztje, és nem az elemzés végső eredménye.
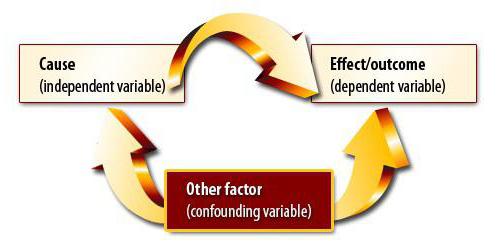
Függőség és okozati összefüggések
Tegyük fel, hogy kiszámítottuk az exportmennyiség és a GDP korrelációs együtthatóját. Kiderült, hogy egyenlő a modulo egységtel. Végül végeztünk korrelációs és regressziós elemzést? Természetesen nem. A kapott eredmény egyáltalán nem jelenti azt, hogy a GDP exporton keresztül kifejezhető. Még nem bizonyítottuk az indikátorok közötti okozati összefüggést. Korrelációs-regressziós elemzés - az egyik változó értékének előrejelzése egy másik alapján. Meg kell azonban értenie, hogy gyakran sok tényező befolyásolja a paramétert. Az export határozza meg a GDP-t, de nem csak azt. Más tényezők is vannak. Itt van egy korreláció és egy okozati összefüggés, bár a bruttó hazai termék egyéb alkotóelemeihez igazítva.
Egy másik helyzet sokkal veszélyesebb. Az Egyesült Királyságban felmérést végeztek, amely kimutatta, hogy azok a gyermekek, akiknek a szülei dohányoztak, gyakrabban elkövetők. Ez a következtetés a mutató közötti szoros összefüggésen alapul. De igaz? Először is, a függőség fordított lehet. A szülők a stressz miatt elkezdhetik a dohányzást azzal a ténnyel, hogy gyermekeik folyamatosan átalakulnak és megsértik a törvényeket. Másodszor, mindkét paraméter oka lehet a harmadik. Az ilyen családok alacsony társadalmi osztályba tartoznak, amelyeket mindkét probléma jellemez. Ezért a korreláció alapján nem lehet arra következtetni, hogy okozati összefüggés van-e.
Miért érdemes használni a regressziós elemzést?
A korrelációs függőség magában foglalja a mennyiségek közötti kapcsolatok megtalálását. Az okozati viszony ebben az esetben a színfalak mögött marad. A korrelációs és a regressziós elemzés feladatai csak egybeesnek azzal, hogy megerősítik a kapcsolat fennállását a két mennyiség értékei között. A kutató azonban kezdetben nem veszi figyelembe az okozati kapcsolat lehetőségét. A regressziós elemzésnek mindig két változója van, amelyek közül az egyik függ. Ez több szakaszban zajlik:
- A megfelelő modell kiválasztása a legkisebb négyzetek módszerével.
- Egy olyan egyenlet származtatása, amely leírja a független változó változásának a másikra gyakorolt hatását.
Például, ha tanulmányozzuk az életkor növekedését az emberi növekedésre, akkor a regressziós elemzés segíthet előre jelezni az évek során bekövetkező változásokat.
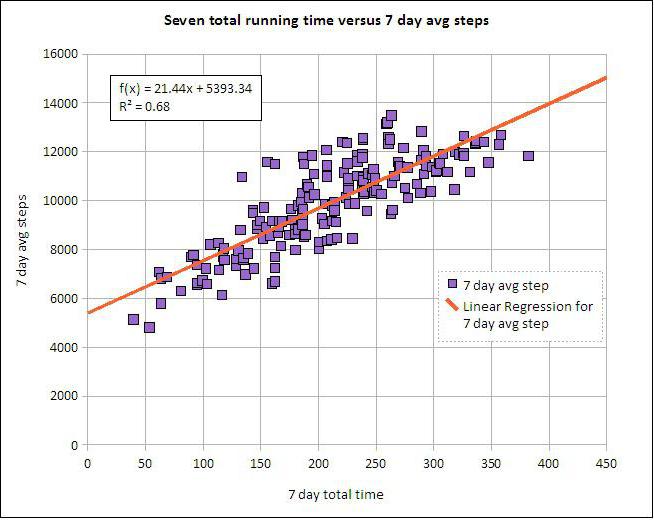
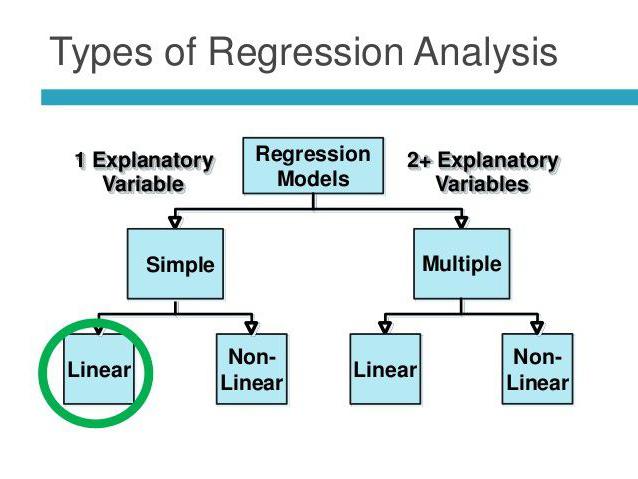
Lineáris és többszörös regresszió
Tegyük fel, hogy X és Y két kapcsolódó változó. A regressziós elemzés lehetővé teszi, hogy az egyik nagyságát a másik értéke alapján megjósoljuk. Például az érettség és az életkor függő tünetek. A köztük fennálló kapcsolat lineáris regresszióval tükröződik. Valójában kifejezheti X-et Y-n keresztül vagy fordítva. De gyakran csak a regressziós vonalak helyesek. Az elemzés sikere nagyban függ a független változó helyes meghatározásától. Például két mutatónk van: hozam és csapadék. A mindennapi tapasztalatok alapján világossá válik, hogy az első a másodiktól függ, és nem fordítva.
A többszörös regresszió lehetővé teszi egy ismeretlen érték kiszámítását három vagy több változó értékei alapján. Például a rizs hozama egy hektár földön függ a gabona minőségétől, a talaj termékenységétől, a műtrágyától, a hőmérséklettől és az esőktől. Ezek a paraméterek befolyásolják a teljes eredményt. A modell egyszerűsítése érdekében a következő feltételezéseket használjuk:
- A független és befolyásoló tulajdonságok közötti kapcsolat lineáris.
- A multiklinearitás ki van zárva. Ez azt jelenti, hogy a függõ változók nincsenek összekapcsolva.
- A számsorok homoskedaszticitása és normalitása.
A korrelációs és regressziós elemzés alkalmazása
Három fő eset fordul elő ennek a módszernek a használatához:
- A mennyiségek közötti alkalmi kapcsolatok tesztelése. Ebben az esetben a kutató meghatározza a változó értékeit, és megállapítja, hogy befolyásolják-e a függő változó változását. Például adhat az embereknek különböző adagokat alkoholt, és megmérheti vérnyomását. Ebben az esetben a kutató biztosan tudja, hogy az első oka a másodiknak, és nem fordítva. A korrelációs-regressziós analízis lehetővé teszi a két változó közötti közvetlen arányos lineáris kapcsolat felismerését, és egy képletből származik, amely leírja azt. Ebben az esetben a teljesen különböző mértékegységekben kifejezett értékeket lehet összehasonlítani.
- Két változó közötti kapcsolat megkeresése anélkül, hogy okozati összefüggést kiterjesztnénk rájuk. Ebben az esetben nincs különbség, hogy a kutatót milyen méretűnek nevezi függőnek. Sőt, a valóságban kiderül, hogy a harmadik változó mindkettőt érinti, ezért arányosan változnak.
- Az egyik mennyiség értékének kiszámítása a másik alapján Egy olyan egyenletre épül, amelyben az ismert számok helyettesítve vannak.
Így a korrelációs elemzés magában foglalja a kapcsolat (nem okozati) megtalálását a változók között, és a regressziós elemzés ezt magyarázza, gyakran egy matematikai függvény felhasználásával.








