A regressziós analízis egy statisztikai módszer egy véletlenszerű változó függőségének tanulmányozására

A statisztikai modellezés során a regressziós analízis egy olyan tanulmány, amelyet a változók közötti kapcsolat felmérésére használnak. Ez a matematikai módszer számos más módszert is magában foglal több változó modellezésére és elemzésére, ha a hangsúly a függő változó és egy vagy több független közötti kapcsolatra koncentrál. Pontosabban, a regressziós elemzés segít megérteni, hogyan változik egy függő változó tipikus értéke, ha az egyik független változó megváltozik, míg a többi független változó rögzített marad.

A célbecslés minden esetben a független változók függvénye, és regressziós függvénynek nevezzük. A regressziós analízis szempontjából az is érdekes, hogy a függő változó változását a regresszió függvényében jellemezzük, amelyet egy valószínűség-eloszlás felhasználásával lehet leírni.

Regressziós elemzési feladatok

Ezt a statisztikai kutatási módszert széles körben használják az előrejelzésekhez, ahol alkalmazásuk jelentős előnnyel jár, de néha illúziókhoz vagy hamis kapcsolatokhoz vezethet, ezért javasoljuk, hogy körültekintően használja ezt a kérdést, mivel például a korreláció nem jelenti okozati összefüggést.

Számos módszert fejlesztettek ki a regressziós elemzés elvégzésére, például a parametrikus lineáris és a legkisebb négyzetek regresszióját. Lényegük az, hogy a regressziós függvényt véges számú ismeretlen paraméter határozza meg, amelyeket az adatokból becsülnek meg. A nem paraméteres regresszió lehetővé teszi, hogy annak funkciói egy bizonyos függvénykészletben rejljenek, amelyek végtelenek lehetnek dimenziósak.

Statisztikai kutatási módszerként a regressziós elemzés a gyakorlatban az adatgyűjtési folyamat formájától és attól függ, hogy hogyan viszonyul a regressziós megközelítéshez. Mivel az adatfolyamat valódi formája általában ismeretlen számot generál, az adatok regressziós elemzése gyakran bizonyos mértékben függ a folyamat feltételezéseitől. Ezeket a feltételezéseket néha ellenőrizni kell, ha elegendő adat áll rendelkezésre. A regressziós modellek gyakran akkor is hasznosak, ha a feltételezéseket mérsékelten megsértik, bár nem tudnak maximális hatékonysággal működni.

Szűkebb értelemben a regresszió kifejezetten a folyamatos válaszváltozók értékelésére vonatkozhat, ellentétben az osztályozásban alkalmazott diszkrét válaszváltozókkal. A folyamatos kimeneti változó esetét metrikus regressziónak is nevezzük annak megkülönböztetése érdekében a kapcsolódó problémáktól.

A történet

A regresszió legkorábbi formája a közismert legkisebb négyzetek módszer. A Legendre 1805-ben és a Gauss 1809-ben tette közzé. Legendre és Gauss ezt a módszert alkalmazta a csillagászati ​​megfigyelések alapján a test körül a Nap körüli testek pályájának meghatározására (elsősorban üstökösök, de később újra felfedezett kisebb bolygók). Gauss 1821-ben közzétette a legkisebb négyzetek elméletének továbbfejlesztését, beleértve a Gauss-Markov tétel változatát.

A „regresszió” kifejezést Francis Galton hozta létre a 19. században egy biológiai jelenség leírására. A lényeg az volt, hogy az ősök növekedéséből származó leszármazottak növekedése általában a normál átlaghoz csökken.Galton számára a regressziónak csak ez a biológiai jelentése volt, ám késõbb Udney Yule és Karl Pearson folytatta munkáját, és általánosabb statisztikai kontextusba vitték. Yule és Pearson munkájában a válaszváltozók és a magyarázó változók együttes eloszlását Gaussiannak tekintik. Ezt a feltételezést Fisher elutasította 1922 és 1925 munkáiban. Fisher javasolta, hogy a válaszváltozó feltételes eloszlása ​​Gauss-féle, de az eloszlás nem lehet. Ebben a tekintetben Fischer feltételezése közelebb áll az 1821-es Gauss-megfogalmazáshoz. 1970-ig a regressziós elemzés eredményének megszerzése néha akár 24 órát is igénybe vett.

A regressziós elemzési módszerek továbbra is az aktív kutatás területe. Az utóbbi évtizedekben új módszereket fejlesztettek ki a megbízható regresszióra; regresszió korrelált válaszokkal; regressziós módszerek a hiányzó adatok különféle típusainak befogadására; nem paraméteres regresszió; Bayes-féle regressziós módszerek; regressziók, amelyekben az előrejelző változókat hibával mérik; regresszió több előrejelzővel, mint megfigyeléssel, valamint okozati következtetések a regresszióval.

Regressziós modellek

A regressziós elemzési modellek a következő változókat tartalmazzák:

• Ismeretlen paraméterek, amelyeket béta-ként jelölnek, amelyek lehet skalár vagy vektor.
• Független változók, X.
• Függő változók, Y.

A tudomány különféle területein, ahol regressziós elemzést alkalmaznak, különböző kifejezéseket használnak függő és független változók helyett, de a regressziós modell minden esetben az Y és X függvényekre vonatkozik.

A közelítés általában E (Y | X) = F (X, β) formában történik. A regressziós elemzés elvégzéséhez meg kell határozni az f függvény típusát. Ritkábban az Y és X közötti kapcsolat ismeretén alapul, amelyek nem támaszkodnak az adatokra. Ha ilyen ismeretek nem állnak rendelkezésre, akkor rugalmas vagy kényelmes F formátumot kell választani.

Y függő változó

Tegyük fel, hogy az ismeretlen β paraméterek vektorának k hossza van. A regressziós elemzés elvégzéséhez a felhasználónak információkat kell szolgáltatnia az Y függő változóról:

• Ha N formátumú adatpont (Y, X) van, ahol N

• Ha pontosan N = K megfigyelése és az F függvény lineáris, akkor az Y = F (X, β) egyenlet pontosan, és nem körülbelül. Ez az N-egyenletek egy sorának az N-ismeretlennel (β elemekkel) történő megoldásához vezet, amelynek egyedi megoldása van, mindaddig, amíg X lineárisan független. Ha F nemlineáris, akkor a megoldás nem létezik, vagy létezik sok megoldás.
• A leggyakoribb az a helyzet, amikor N> az adatokra mutat. Ebben az esetben elegendő információ van az adatokban ahhoz, hogy meghatározzuk az β egyedi értékét, amely legjobban megfelel az adatoknak, és az adatokra alkalmazva a regressziós modell a β túldeterminált rendszerének tekinthető.

Az utóbbi esetben a regressziós elemzés eszközöket kínál a következőkre:

• Megoldások keresése ismeretlen β paraméterekre, amelyek például minimalizálják a mért és a becsült Y értékek közötti távolságot.
• Bizonyos statisztikai feltevések szerint a regressziós analízis felesleges információkat használ fel az ismeretlen β paraméterekre és az Y függõ változó becsült értékeire vonatkozóan.

Szükséges számú független mérés

Vegyünk egy regressziós modellt, amelynek három ismeretlen paramétere van: β₀, β₁ és p₂. Tegyük fel, hogy a kísérleti személy 10 mérést hajt végre az X vektor független változójának azonos értékével.Ebben az esetben a regressziós elemzés nem nyújt egyedi értékkészletet. A legjobb, ha megteszi a függő Y változó átlagát és szórását. Ha két különböző X értéket azonos módon mér, akkor elegendő adatot kaphat két ismeretlen regresszióhoz, de három vagy több ismeretlenhez nem.

Ha a kísérletező méréseit az X vektor független változójának három különböző értékén végeztük, akkor a regressziós analízis egyedi becslések készlete a β három ismeretlen paraméterére.

Általános lineáris regresszió esetén a fenti állítás egyenértékű azzal a követelménnyel, hogy az X mátrixot^TX visszafordítható.

Statisztikai feltételezések

Ha az N mérések száma nagyobb, mint az ismeretlen k paraméterek száma és az ε mérési hiba_én, majd rendszerint a mérésekben szereplő információk feleslegét elosztják és felhasználják az ismeretlen paraméterekre vonatkozó statisztikai előrejelzésekhez. Ezt az információfelesleget nevezik a regresszió szabadságának.

Alapvető feltételezések

A regressziós elemzés klasszikus feltételezései a következők:

• A minta reprezentatív a következtetés becslésénél.
• A hiba egy véletlenszerű változó, amelynek átlagos értéke nulla, amely a magyarázó változóktól függ.
• A független változókat hiba nélkül mérjük.
• Független változóként (prediktorként) lineárisan függetlenek, vagyis nem lehet egyetlen prediktort kifejezni a többiek lineáris kombinációja formájában.
• A hibák nem korreláltak, azaz az átlós hibák kovariancia mátrixa és az egyes nem nulla elemek a hiba varianciája.
• A hiba szórása a megfigyelések szerint állandó (homoskedaszticitás). Ha nem, akkor a súlyozott legkisebb négyzetek módszerét vagy más módszert is használhatja.

Ezek a legkisebb négyzetek becsléséhez szükséges feltételek rendelkeznek a szükséges tulajdonságokkal, különösen ezek a feltevések azt jelentik, hogy a paraméterbecslések objektívek, következetesek és hatékonyak, különösen, ha a lineáris becslések osztályában figyelembe veszik. Fontos megjegyezni, hogy a bizonyítékok ritkán felelnek meg a feltételeknek. Vagyis a módszert akkor is használják, ha a feltételezések nem igazak. A feltevések változata néha felhasználható annak mérésére, hogy ez a modell mennyire hasznos. Ezen feltevések közül sok enyhíthető fejlettebb módszerekkel. A statisztikai elemzési jelentések általában magukban foglalják a tesztek elemzését a mintaadatok és a modellhasználat módszertana alapján.

Ezenkívül a változók bizonyos esetekben a pontokban mért értékekre utalnak. A statisztikai feltételezéseket sértő változókban térbeli tendenciák és térbeli autokorreláció fordulhat elő. Az ilyen adatokkal a földrajzi súlyozott regresszió az egyetlen módszer.

Lineáris regressziós elemzés

Lineáris regresszió esetén az a tulajdonság, hogy a függõ változó, amely Y_éna paraméterek lineáris kombinációja. Például egy egyszerű lineáris regresszió esetén egy független x változót használunk az n-pontok modellezésére_énés két paraméter, β₀ és p₁.

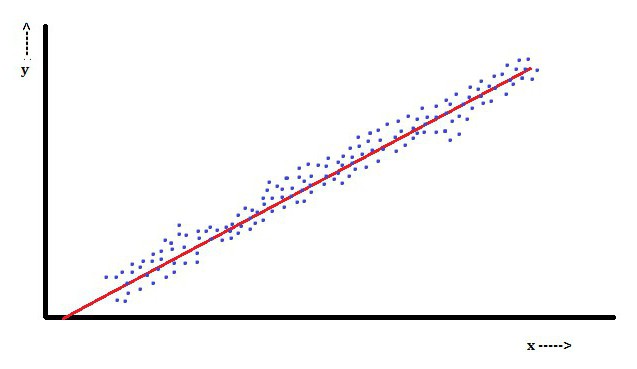
Több lineáris regresszióval számos független változó vagy funkciójuk létezik.

Egy populációból véletlenszerű mintavétellel annak paraméterei lehetővé teszik a lineáris regressziós modell példájának megszerzését.

Ebben a vonatkozásban a legkevesebb négyzet módszer a legnépszerűbb. Ezzel paraméterbecsléseket kapunk, amelyek minimalizálják a maradék négyzet összegét. Ennek a függvénynek a minimalizálása (ami egy lineáris regresszióra jellemző) normál egyenletek halmazához és egy lineáris egyenlet halmazához vezet paraméterekkel, amelyeket a paraméterek becslésének megoldandására oldunk meg.

Feltételezve, hogy a populáció hibája általában terjed, a kutató ezeket a standard hibák becsléseit felhasználhatja konfidencia-intervallumok létrehozására és a paraméterekkel kapcsolatos hipotézisek tesztelésére.

Nemlineáris regressziós elemzés

Egy példa, amikor a függvény nem lineáris a paraméterekhez viszonyítva, azt jelzi, hogy a négyzetek összegét iterációs eljárással kell minimalizálni. Ez számos olyan komplikációt vezet be, amelyek meghatározzák a lineáris és a nemlineáris legkisebb négyzetek módszerének különbségeit. Következésképpen a nemlineáris módszerrel végzett regressziós elemzés eredményei néha kiszámíthatatlanok.

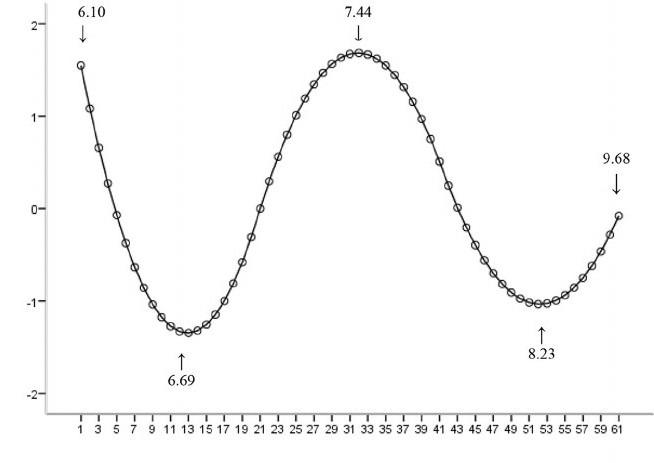
A teljesítmény és a minta méretének kiszámítása

Itt rendszerint nincs következetes módszer a megfigyelések számának összehasonlítására a modellben szereplő független változók számával összehasonlítva. Az első szabályt Good és Hardin javasolta, és úgy néz ki, mint N = t ^ n, ahol N a minta mérete, n a független változók száma, és t a megfigyelések száma, amely a kívánt pontosság eléréséhez szükséges, ha a modell csak egy független változóval rendelkezik. Például egy kutató egy lineáris regressziós modellt épít fel olyan adatkészlet felhasználásával, amely 1000 beteget tartalmaz (N). Ha a kutató úgy dönt, hogy öt megfigyelésre van szükség a vonal (m) pontos meghatározásához, akkor a modell által támogatható független változók maximális száma 4.

Egyéb módszerek

Annak ellenére, hogy a regressziós modell paramétereit általában a legkisebb négyzetek módszerével becsülik meg, vannak más módszerek is, amelyeket sokkal ritkábban használnak. Például ezek a következő módszerek:

• Bayes-módszer (például Bayes-féle lineáris regressziós módszer).
• A százalékos regresszió olyan helyzetekben használatos, amikor a százalékos hibák csökkentését célszerűbbnek tekinteni.
• A legkisebb abszolút eltérés, amely stabilabb olyan kimenetek jelenlétében, amelyek kvantitatív regressziót eredményeznek.
• Nem paraméteres regresszió, amely számos megfigyelést és számítást igényel.
• A tanulási mutató távolsága, amelyet egy adott bemeneti térben jelentős metrikus távolság keresése céljából tanulmányoznak.

szoftver

Az összes főbb statisztikai szoftvercsomagot a legkisebb négyzetek regressziós elemzésével végezzük. Egyszerű lineáris regresszió és többszörös regresszióanalízis használható néhány táblázatkezelő alkalmazásban, valamint néhány számológépben. Bár sok statisztikai szoftvercsomag képes különféle típusú nem paraméteres és megbízható regresszióra, ezek a módszerek kevésbé szabványosítottak; a különböző szoftvercsomagok különböző módszereket valósítanak meg. Speciális regressziós szoftvert fejlesztettek ki olyan területeken, mint például a vizsgálati elemzés és az idegkép.