Cobb-Douglas termelési funkció

A gazdaságban a termelés alatt az erőforrások és a technológiák felhasználását értjük annak érdekében, hogy megkapjuk az eladható terméket. Ez az a folyamat, amellyel egy termék létrehozására vagy egy szolgáltatás nyújtására kerül sor, amely a vevő számára hasznos. A piaci kereslet és kínálat meghatározzák árukat. A kiadott áruk mennyiségét és végső soron értéküket a termelés és a termelési funkció mutatja. A keresletet az ár és más tényezők befolyásolják. Az utóbbiak tartalmazzák a fogyasztói jövedelmet, ízlésüket, a helyettesítő áruk költségeit.

A gazdasági jólét a termelési folyamat során jön létre. Ez azt jelenti, hogy minden gazdasági tevékenység közvetlen vagy közvetett célja az emberi igények kielégítése. Az állam gazdasági jóléte az utóbbitól függ. Minél nagyobb a szükségletek kielégítésének mértéke és a középosztály aránya a népességben, annál erősebb a nemzeti fejlődés. A termelési funkció magyarázza az emberek jólétének javulását a termelési folyamatban.

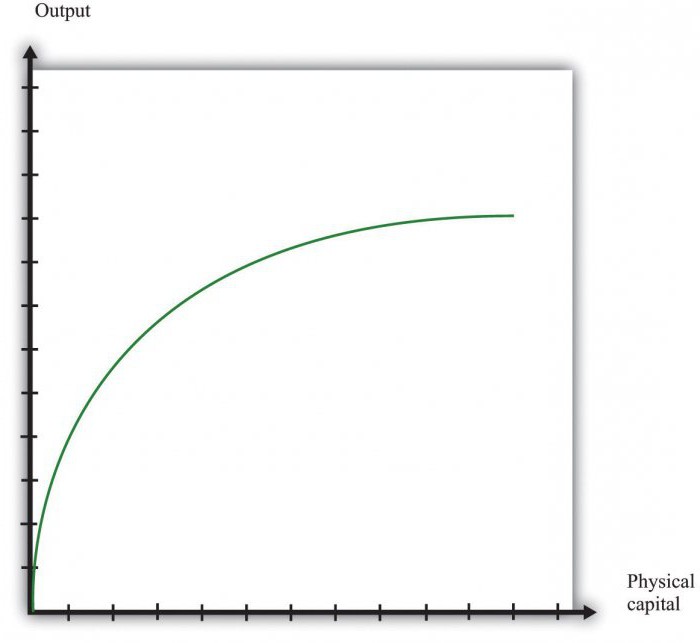
Általános információk

A gazdaság termelési funkciója a tényleges outputot az erőforrásokhoz köti, amelyeket a beszerzési folyamatba fektettek be. Ez a koncepció kulcsfontosságú a neoklasszikus elméletekben. A termelési függvényt használják a határérték és az általános hatékonyság meghatározására. Ez utóbbi az összes gazdasági kutatás sarokköve. A termelési funkció elsődleges feladata a termelési tényezők felhasználásának hatékonyságának meghatározása és a kapott jövedelem eloszlása ​​a felmerülő technológiai problémák figyelembevétele nélkül.

A makroökonómiaban az aggregált mutatókat kiszámítják annak megértése érdekében, hogy hogyan alakul a gazdasági növekedés: különösen a tőke felhalmozódása vagy a technológia fejlesztése miatt. Meg kell jegyezni, hogy vannak tudósok, akik elutasítják az aggregált termelési funkció fogalmát, ám ez a szempont nem széles körben elterjedt.

A termelési funkciók elmélete

Szigorú értelemben a termelést nem lehet matematikailag ábrázolni, mint a befektetett források összegét vagy eredményét. Mivel a termelési tényezők mindegyike felhasználható számos termék létrehozására. A matematikai meghatározás teljesítése érdekében feltételezzük, hogy a termelési függvény az áruk maximális lehetséges felszabadítását jeleníti meg egy adott erőforrás-készletből. Így azt a tényezők minimális arányát jelöli, amely szükséges a megállapodás szerinti termékmennyiség létrehozásához. A lehető legnagyobb mértékű kibocsátás feltételezése lehetővé teszi a közgazdászoknak, hogy kivonuljanak a technológiai és vezetői problémáktól, és figyelmüket kizárólag az aggregált hatékonyság problémájára összpontosítsák. Megoldása lehetővé teszi annak megértését, hogy az erőforrások milyen mértékben helyettesíthetők egy másikval. A vállalat termelési funkciója nem tükrözi a kibocsátás és az érintett tényezők közötti monetáris kapcsolatot, bár magában foglalja a fizikai mennyiségeket. A termelés ára és a tényezők költségei kívül esnek.

A termelési funkciók típusai

A kibocsátás különféle tényezőktől és az egész nemzetgazdaságtól való függőségét jellemző gazdasági és matematikai modellek a következő mutatókat vehetik figyelembe: a termelés volumene (értékben vagy természetben), a rögzített tőke és a felhasznált pénzeszközök, a munkaerő, az energiafogyasztás, a gépek száma és berendezés.A termelési funkciók három csoportja van:

1. Egyváltozós. Ez a csoport magában foglalja a lineáris, parabolikus, erő és exponenciális funkciót.
2. Két tényező. Ez a csoport Leontief, Cobb-Douglas, Allen, Solow funkcióit foglalja magában, lineáris, a felhasznált erőforrások cseréjének állandó rugalmasságával.
3. Multifaktoriális.

A Leontief funkcióval teljesen automatizált vagy kis léptékű folyamatok modellezhetők. Ez nem engedélyezi a termelés egységenkénti erőforrások szigorúan meghatározott technológiai normáitól való eltérést. A Cobb-Douglas függvény közepes méretű folyamatokat ír le (ipari társulásoktól egész iparáig). Használatának fő feltétele a stabil és viszonylag stabil működés. Allen funkciója olyan kis léptékű folyamatokat ír le, amelyekben az erőforrások feldolgozási lehetőségei korlátozottak. Olyan helyzetekre szánják, amikor az egyes tényezők túlzott növekedése negatív hatással van a kibocsátásra. A Solow funkció használata bármilyen méretű modellező rendszer esetén ajánlott. Használatának fő feltétele a pótlási ráta függése az erőforrások arányától.

Cobb-Douglas a közgazdaságtanban működik

A termelés két fő tényezője a munkaerő és a tőke. Egy bizonyos arányban történő kombinációjuk lehetővé teszi egy termék létrehozását. A Cobb-Douglas termelési funkció tükrözi a munkaerő és a tőke közötti technológiai összefüggést egy bizonyos mennyiségű áru előállításakor. Ez a modell két tényező, és statisztikailag két tudós ellenőrizte, akinek a vezetéknevét nevezték, 1927-1947-ben. A „Cobb-Douglas termelési funkció” kifejezés néha szűkebb jelentéssel bír, és állandó skálamegtérülést jelez (ebben az esetben b = 1-a a fő képletben).

Alapképlet

A Douglas-Cobb termelési funkció tükrözi egy adott termék termelésének két tényezõ: munkaerõ és tôke arányától való függését. Leg általánosabb formájában a képlet a következő: Y = A * L^b* K^egy, ahol a betűk a következő mutatókat jelzik:

• Y a termelés teljes mennyisége (az összes ebben az évben kiadott áru valós értéke);
• L a munka hozzájárulása (egy adott időszakban ledolgozott ember-órák száma);
• K - a felhasznált tőke összege (gépek, berendezések és épületek valós értéke);
• A - a tényezők teljes termelékenysége;
• a és b a munka és a tőke rugalmassága (ezeket az értékeket a rendelkezésre álló technológiák határozzák meg);

A Cobb-Douglas termelési funkciót statisztikák alapján fejlesztették ki. Megmutatták, hogy a fejlett országokban a munka és a tőke hozzájárulásának aránya idővel állandó volt. Manapság sok tudósnak kétséges ebben a helyzetben.

A termelési tényezők rugalmassága

Az a) és b) paraméterek fontos szerepet játszanak az áruk becsült teljesítményének kiszámításában a Cobb-Douglas képlettel. A tényezők rugalmassága tükrözi, hogy arányuk változása hogyan befolyásolja a fizikai termelést, ceteris paribus. Például, ha a = 0,45, akkor a munkaerő-felhasználás 1% -os növekedése az árukiadás megközelítőleg 0,45% -kal történő növekedését eredményezi.

Vegyük figyelembe az értékek három fő esetét, amelyek a képletben együtthatókat vehetnek fel:

• a + b = 1. Ebben az esetben úgy véljük, hogy a termelési funkciónak állandó megtérülése van a skála szempontjából. Ez azt jelenti, hogy a tőke és a munkaerő felhasználásának 100% -os növekedése az áruk teljes kibocsátásának megkétszereződéséhez vezet;
• a + b;
• a + b> 1. Ez az eset a méretarányos visszatérés csökkenésével jár.

A körülmények között tökéletes verseny valamint a munka és a tőke rugalmasságának egyenlősége, az a és b együtthatók az egyes tényezők részesedését mutatják a termelés teljes volumenében.

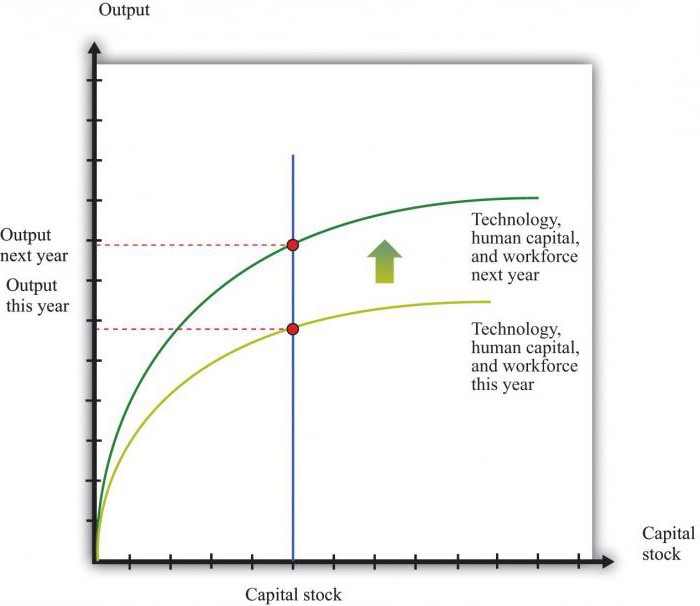
Képletfejlesztési történelem

Paul Douglas kezdetben tanulmányozta az emberórák hozzájárulását és a tőke mennyiségét a kibocsátáshoz.Funkcionális kapcsolatot keresett ezen mutatók között. Beszélt kollégájával, Charles Cobb-nal, és együtt származtak egy képletet egy együtthatóval: Y = A * L^b* K^1-b. Korábban ezt az egyenlőséget Knut Wicksell már alkalmazta. A legkisebb négyzetek módszerével becsülve a számítás eredményét, Douglas megállapította, hogy a munkaerő-kitevő 0,75. Később megerősítette a Nemzeti Gazdaságkutatási Iroda számítása. A képlet kidolgozása során végzett további munkák azt mutatták, hogy a munkaerő és a tőke kitevői nem lehetnek állandóak. Ennek eredményeként ez lehetővé tette a termelékenység pontosabb meghatározását.

Ennek a modellnek a legnagyobb problémája az volt, hogy a kiadás gyártási funkciója túl kevés statisztikai adatokon alapult, így nem lehetett teljes mértékben megbízni. Douglas úgy döntött, hogy az amerikai népszámlálás adatait használja, amelyek számos területet lefedtek és jelentős mennyiségű megfigyelést nyújtottak. A tudós 1947-ben az Egyesült Államok és más országok számára végzett új kutatásainak eredményeit mutatta be az Amerikai Gazdasági Egyesület ülésén, amelynek elnöke volt. Hamarosan Douglas politikus lett, ám a rossz egészségi állapot nem tette lehetővé neki, hogy tovább fejlessze koncepcióját. Húsz évvel később azonban produkciós funkcióját prominens közgazdászok - Paul Samuelson és Robert Solow népszerűsítették.

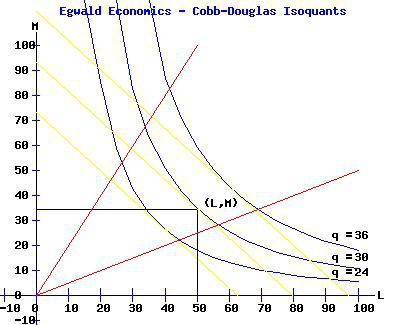
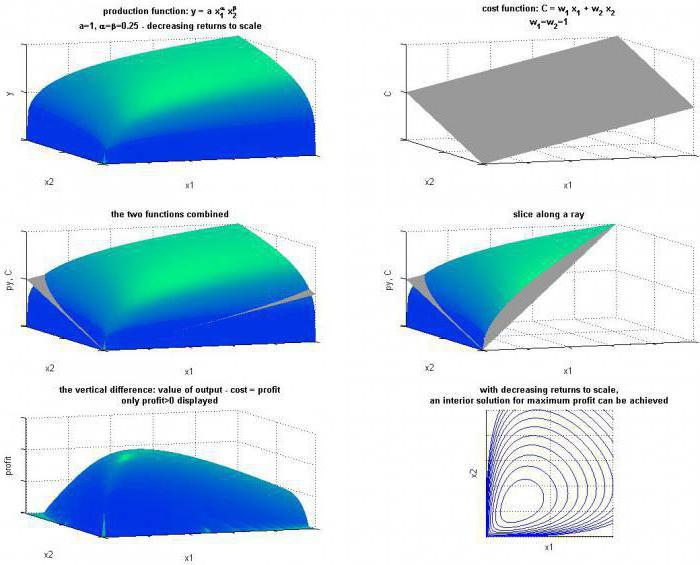
Grafikus kép

A munkaerő- és tőkeköltségek változásának a termelés mennyiségére gyakorolt ​​hatása nemcsak képletekkel, hanem izo-kvantákkal is kimutatható. Ez utóbbi olyan görbék, amelyek az erőforrások különböző kombinációit mutatják, amelyek ugyanazon output biztosításához használhatók. Az izokváns térkép egy alternatív módszer a termelési funkció leírására. Minél távolabb van a görbe a koordináta eredetétől, annál nagyobb a kimeneti térfogat a tényezők kombinációján keresztül. Bármely izoquantum szög koefficiense kifejezhető arányosan, ha az egyik erőforrás helyettesíthető egy másikval a gyártási folyamat során. Abszolút értéke megegyezik a technológiai helyettesítés sebességével.

Problémák és kritika

A nemzetgazdaság egy komplex rendszer, amely számos elemet és azok kapcsolatát tartalmazza. Ezért annyira nehéz, ha egyáltalán lehetséges, egy ideális modellt felépíteni. A Cobb-Douglas funkció használatának fő problémái két területre oszthatók:

1. Dimenziós elemzés. Az osztrák közgazdasági iskola képviselői a pontos mutatók hiánya miatt bírálták a Cobb-Douglas modellt. Azt állították, hogy a képletnek nincs értelmes és gazdasági szempontból megalapozott mérési intézkedése. Más közgazdászok azonban a Barnett-re adott válaszként kijelentették, hogy a rendelkezésre álló mutatók nem kevésbé pontosak, mint a fizikában széles körben alkalmazott hőmérsékletek vagy távolság négyzetek logaritmusai.
2. Mikrogazdasági okok hiánya. A Cobb-Douglas termelési funkcionális tényezőit nem a mérnöki, technológiai vagy folyamatirányítási ismeretek alapján fejlesztették ki. Éppen ellenkezőleg, azt kezdték használni, mert gyönyörű matematikai jellemzőkkel bír, különösen az egyes tényezők hasznosságának csökkenő törvénye, és az a tulajdonság, hogy a termelési költségek a teljes költség állandó részét képezik. És erre nincs mikrogazdasági ok. Manapság sok közgazdász megkísérli modelleit az egyének viselkedése alapján építeni, ahelyett, hogy elképzeléseiket az egész gazdaságra kényszerítené. A modern közgazdászok (különösen a neo-keynesiaiak) azonban a mikrotól kezdve kidolgozták a munka és a tőke termelési funkcióit, amelyek csak Cobb és Douglas következtetéseit erősítik meg. Mindazonáltal nem lehet azt állítani, hogy a modell alkalmazhatósága az egyes iparágakban automatikusan azt jelenti, hogy felhasználni kell azt az aggregált gazdaságban.

Alkalmazási területek

A nő kritikája ellenére a Cobb-Douglas funkció széles körben elterjedt a közgazdaságtanban. Használható az (u) segédprogram megtalálásához. Ha x1 és x2 az első és a második áru fogyasztásának mennyisége, akkor u = x1^egy* x2^b.

A termelés mint a vállalkozáson belüli folyamat

A gyártási folyamat több szakaszra osztható. Mindegyiknek megvan a maga logikája, célja és kulcsa. Fontos, hogy külön tanulmányozzuk őket, de értsük meg, hogy minden szakasz az egész része. A vállalkozáson belül a következő folyamatok különböznek egymástól:

• Az igazi.
• Jövedelem-felosztás.
• Gyártás.
• Monetáris.
• Piaci érték.

Nagyobb teljesítmény és teljesítmény

Bármely vállalkozás célja a saját jövedelmezőségének növelése. Ehhez vagy növelnie kell a gyártott termékek egységszámát, vagy csökkentenie kell az erőforrások felhasználását. A kibocsátás növekedését általában a múltbeli időszak százalékában mutatják. A termelési funkció csak az áruk gyártásának valós folyamatát tükrözi a vállalkozásnál. Ugyanakkor bemutatja a jövedelemszerzés mechanizmusát a felszabadítás során. Két elemből áll: az áruk mennyiségének és a termelékenységnek a változása.

A gazdaságban általában csak két fő folyamata van - a termelés és a fogyasztás. És ugyanannyi fő piaci szereplő - eladó és vevő. Az állam és lakói jóléte a termelés hatékonyságától és a szereplők közötti kommunikációtól függ. A Cobb-Douglas formula az összesített termelés első funkciója. Ennek segítségével nemcsak a kisméretű folyamatok, hanem az egész iparág modellezése is lehetővé vált. Megjelenése a makroökonómia fejlődésének új szakaszát jelölte meg, mivel ez lehetővé tette a termelés hatékonyságának értékelését az állam teljes nemzetgazdaságában.