Le niveau de signification des statistiques est un indicateur important reflétant le degré de confiance dans l'exactitude et la véracité des données reçues (prévues). Le concept est largement utilisé dans divers domaines: de la recherche sociologique au test statistique d'hypothèses scientifiques.

La définition
Le niveau de signification statistique (ou résultat statistiquement significatif) indique quelle est la probabilité d'apparition accidentelle des indicateurs étudiés. La signification statistique générale du phénomène est exprimée par le coefficient p-value (p-level). Dans toute expérience ou observation, il est probable que les données obtenues soient dues à des erreurs d'échantillonnage. Ceci est particulièrement vrai pour la sociologie.
C'est-à-dire qu'une statistique est statistiquement significative et que sa probabilité d'occurrence accidentelle est extrêmement faible ou tend à atteindre des extrêmes. Extreme dans ce contexte est considéré le degré d'écart des statistiques par rapport à l'hypothèse nulle (hypothèse dont la cohérence est vérifiée avec les données de l'échantillon obtenues). Dans la pratique scientifique, le niveau de signification est choisi avant la collecte des données et, en règle générale, son coefficient est de 0,05 (5%). Pour les systèmes où les valeurs précises sont extrêmement importantes, cet indicateur peut être inférieur ou égal à 0,01 (1%).
Le fond
Le concept de niveau de signification a été introduit par le statisticien et généticien britannique Ronald Fisher en 1925, lorsqu'il développa une méthodologie pour tester des hypothèses statistiques. Lors de l'analyse d'un processus, il existe une certaine probabilité de certains phénomènes. Des difficultés surviennent lorsque vous travaillez avec des probabilités faibles (ou peu évidentes) qui relèvent du concept "d'erreur de mesure".
En travaillant avec des statistiques qui ne sont pas assez spécifiques pour être vérifiées, les scientifiques ont été confrontés au problème de l'hypothèse nulle, qui «interfère» avec de petites quantités. Fisher a suggéré de définir pour de tels systèmes probabilité d'événements 5% (0,05) en tant que tranche sélective pratique, vous permettant de rejeter l'hypothèse nulle dans les calculs.
L'introduction d'un coefficient fixe
En 1933, les scientifiques Jerzy Neumann et Egon Pearson recommandaient préalablement (avant la collecte de données) d'établir un certain niveau de signification. Des exemples d'utilisation de ces règles sont clairement visibles lors de l'élection. Supposons qu'il y ait deux candidats, l'un très populaire et l'autre peu connu. De toute évidence, le premier candidat remporte les élections et les chances du second sont généralement nulles. Ils s'efforcent - mais pas à égalité: il y a toujours une probabilité de force majeure, une information sensationnelle, des décisions inattendues pouvant modifier les résultats électoraux prévus.
Neumann et Pearson ont convenu que le niveau de signification proposé par Fisher de 0,05 (indiqué par le symbole α) est le plus pratique. Cependant, Fisher lui-même en 1956 s'est opposé à la fixation de cette valeur. Il a estimé que le niveau de α devrait être établi en fonction de circonstances spécifiques. Par exemple, en physique des particules, il est 0,01.
Valeur P
Le terme p-value a été utilisé pour la première fois dans les travaux de Brownley en 1960. Le niveau P (valeur p) est un indicateur inversement lié à la vérité des résultats. La valeur p du coefficient le plus élevé correspond au niveau de confiance le plus faible dans l'échantillon de dépendance entre les variables.
Cette valeur reflète la probabilité d'erreur associée à l'interprétation des résultats. Supposons que p-level = 0.05 (1/20). Il montre la probabilité de 5% que la relation entre les variables trouvées dans l'échantillon ne soit qu'une caractéristique aléatoire de l'échantillon.Autrement dit, si cette dépendance est absente, on peut s’attendre à une dépendance identique ou supérieure entre les variables, avec des expériences répétées en moyenne dans chaque vingtième étude. Souvent, le niveau p est considéré comme la «marge acceptable» du niveau d'erreur.
Soit dit en passant, la valeur p peut ne pas refléter la relation réelle entre les variables, mais uniquement une certaine valeur moyenne dans les hypothèses. En particulier, l'analyse finale des données dépendra également des valeurs sélectionnées pour ce coefficient. Avec un p-level = 0,05, il y aura des résultats et avec un coefficient de 0,01, d'autres.
Tester des hypothèses statistiques
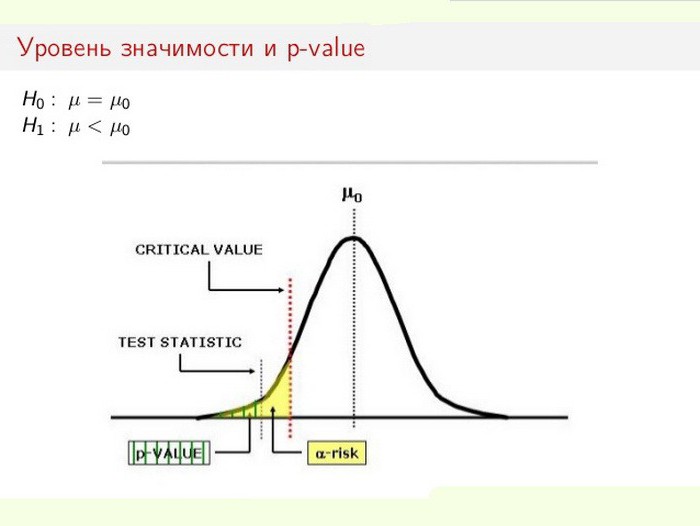
Le niveau de signification statistique est particulièrement important lors du test des hypothèses. Par exemple, lors du calcul d'un test bilatéral, la zone de rejet est divisée de manière égale aux deux extrémités de la distribution de l'échantillon (par rapport à la coordonnée zéro) et la vérité des données est calculée.
Supposons que, lors de la surveillance d'un processus (phénomène) donné, il s'avère que les nouvelles informations statistiques indiquent de petits changements par rapport aux valeurs précédentes. De plus, les différences dans les résultats sont minimes, pas évidentes, mais importantes pour l’étude. Le dilemme se pose devant le spécialiste: les changements ont-ils réellement lieu ou s'agit-il d'erreurs d'échantillonnage (mesures inexactes)?
Dans ce cas, l'hypothèse nulle est soit utilisée, soit rejetée (tout est attribué à une erreur ou la modification du système est reconnue comme un fait accompli). Le processus de résolution du problème repose sur le rapport entre la signification statistique totale (valeur p) et le niveau de signification (α). Si le niveau p <α, l'hypothèse nulle est rejetée. Plus la valeur p est petite, plus la statistique de test est significative.
Valeurs utilisées
Le niveau de signification dépend du matériel analysé. En pratique, les valeurs fixes suivantes sont utilisées:
- α = 0,1 (ou 10%);
- α = 0,05 (ou 5%);
- α = 0,01 (ou 1%);
- α = 0,001 (ou 0,1%).
Plus les calculs sont précis, plus le coefficient α utilisé est faible. Naturellement, les prévisions statistiques en physique, chimie, pharmacie, génétique exigent une plus grande précision que dans les sciences politiques, la sociologie.

Seuils de pertinence dans des domaines spécifiques
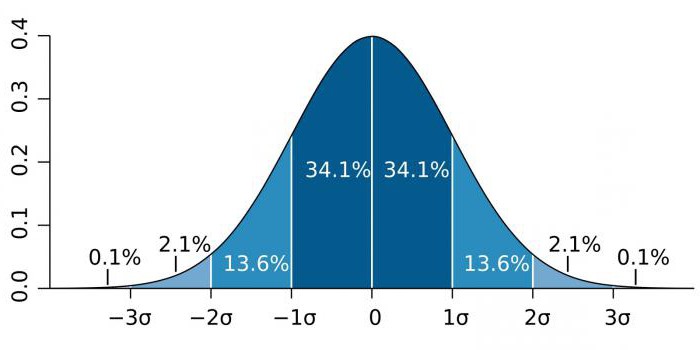
Dans les domaines de haute précision, tels que la physique des particules et les activités de fabrication, la signification statistique est souvent exprimée par le rapport de l'écart type (noté par le coefficient sigma - σ) par rapport à la distribution de probabilité normale (distribution gaussienne). σ est un indicateur statistique qui détermine la dispersion des valeurs d’une certaine valeur par rapport aux attentes mathématiques. Utilisé pour tracer la probabilité d'événements.
En fonction du domaine de connaissance, le coefficient σ varie considérablement. Par exemple, pour prédire l’existence du boson de Higgs, le paramètre σ est égal à cinq (σ = 5), ce qui correspond à la valeur p-value = 1 / 3,5 millions. Dans les études sur les génomes, le niveau de signification peut être de 5 × 10.-8qui ne sont pas rares pour ce domaine.
L'efficacité
Gardez à l'esprit que les coefficients α et p ne sont pas des caractéristiques précises. Quel que soit le niveau de signification dans les statistiques du phénomène étudié, ce n’est pas une base inconditionnelle pour accepter l’hypothèse. Par exemple, plus la valeur de α est faible, plus grande est la probabilité que l'hypothèse établie soit significative. Cependant, il existe un risque d'erreur qui réduit le pouvoir statistique (signification) de l'étude.
Les chercheurs qui se concentrent uniquement sur des résultats statistiquement significatifs peuvent tirer des conclusions erronées. En même temps, il est difficile de revérifier leur travail, car ils utilisent des hypothèses (qui sont en fait les valeurs de α et de p-value). Par conséquent, il est toujours recommandé, avec le calcul de la signification statistique, de déterminer un autre indicateur - l’ampleur de l’effet statistique. L'ampleur d'un effet est une mesure quantitative de la force d'un effet.
