L’analyse de la variance est un ensemble de méthodes statistiques conçues pour vérifier les hypothèses concernant la relation entre certains signes et les facteurs étudiés, sans description quantitative, ainsi que pour établir le degré d’influence des facteurs et leur interaction. Dans la littérature spécialisée, il est souvent appelé ANOVA (du nom anglais Analysis of Variations). Cette méthode a été développée par R. Fisher en 1925.
Types et critères d'analyse de variance
Cette méthode est utilisée pour étudier la relation entre les attributs qualitatifs (nominaux) et une variable quantitative (continue). En fait, il teste l'hypothèse selon laquelle la moyenne arithmétique de plusieurs échantillons est égale. Ainsi, il peut être considéré comme un critère paramétrique pour comparer les centres de plusieurs échantillons à la fois. Si vous utilisez cette méthode pour deux échantillons, les résultats de l'analyse de variance seront identiques à ceux du test t-student. Cependant, contrairement à d’autres critères, cette étude nous permet d’étudier le problème plus en détail.

L'analyse de la variance en statistique est basée sur la loi: la somme des carrés des déviations de l'échantillon combiné est égale à la somme des carrés des déviations intragroupe et de la somme des carrés des déviations intergroupe. Pour l'étude, le test de Fisher est utilisé pour établir la signification de la différence entre les variances intergroupes par rapport aux variances intra-groupe. Cependant, pour cela, les conditions préalables nécessaires sont la distribution normale et l’homoscancasticité (égalité des variances) des échantillons. Faites la distinction entre l'analyse de variance unidimensionnelle (univariée) et multivariée (multivariée). Le premier considère la dépendance de la quantité étudiée sur un attribut, le second - immédiatement sur plusieurs, et vous permet également d'identifier la relation entre eux.
Facteurs
Les facteurs sont appelés circonstances contrôlées qui affectent le résultat final. Son niveau ou méthode de traitement est appelé la valeur qui caractérise la manifestation spécifique de cette condition. Ces chiffres sont généralement donnés dans une échelle nominale ou en série. Les valeurs de sortie sont souvent mesurées à l'aide d'échelles quantitatives ou ordinales. Le problème se pose alors de regrouper les données de sortie dans une série d'observations, qui correspondent approximativement aux mêmes valeurs numériques. Si le nombre de groupes est considéré comme excessivement grand, le nombre d'observations qu'ils contiennent peut être insuffisant pour obtenir des résultats fiables. Si vous prenez le nombre trop petit, cela peut entraîner la perte de nombreuses caractéristiques d'impact sur le système. La manière dont les données sont regroupées dépend du volume et de la nature de la variation des valeurs. Le nombre et la taille des intervalles dans l'analyse unidirectionnelle sont le plus souvent déterminés par le principe des intervalles égaux ou par le principe des fréquences égales.
Analyse des problèmes de variance
Il existe donc des cas où il est nécessaire de comparer deux échantillons ou plus. C'est alors que l'utilisation de l'analyse de la variance est recommandée. Le nom de la méthode indique que les conclusions sont tirées de l’étude des composantes de la variance. L’essence de l’étude est que le changement général de l’indicateur est divisé en composantes qui correspondent à l’action de chaque facteur individuel. Considérez un certain nombre de problèmes qu'une analyse de variance typique résout.
Exemple 1
L'atelier dispose d'un certain nombre de machines-outils - des machines automatiques qui produisent une pièce spécifique. La taille de chaque pièce est une valeur aléatoire, qui dépend des paramètres de chaque machine et des écarts aléatoires qui se produisent lors de la fabrication des pièces.Il est nécessaire de déterminer si les machines sont configurées de manière égale en fonction des dimensions des pièces.
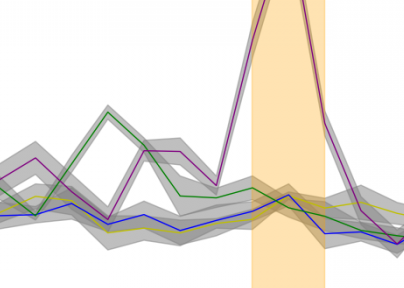
Exemple 2
Lors de la fabrication de l'appareil électrique, différents types de papier isolant sont utilisés: condenseur, électricité, etc. L'imprégnation de l'appareil peut être imprégnée de différentes substances: résine époxy, vernis, résine ML-2, etc. Les fuites peuvent être éliminées sous vide à haute pression, par chauffage. Il peut être imprégné par immersion dans un vernis, sous un courant continu de vernis, etc. L'ensemble de l'appareil électrique est coulé avec un certain composé, pour lequel il existe plusieurs options. Les indicateurs de qualité sont la rigidité diélectrique de l'isolant, la température de surchauffe de l'enroulement en mode de fonctionnement et plusieurs autres. Lors du test du processus technologique de fabrication des appareils, il est nécessaire de déterminer la manière dont chacun des facteurs énumérés affecte les performances de l'appareil.
Exemple 3
Le dépôt de trolleybus dessert plusieurs itinéraires de trolleybus. Différents types de trolleybus fonctionnent pour eux et la collecte des tarifs est collectée par 125 contrôleurs. La direction du dépôt s'intéresse à la question suivante: comment comparer les performances économiques de chaque contrôleur (chiffre d'affaires) en tenant compte de différents itinéraires, de différents types de trolleybus? Comment déterminer la faisabilité économique de la libération d'un type particulier de trolleybus sur un itinéraire particulier? Comment établir des exigences raisonnables en ce qui concerne le montant des revenus générés par le chef de train sur chaque parcours dans différents types de trolleybus?
La tâche de choisir une méthode consiste à obtenir le maximum d’informations sur l’impact sur le résultat final de chaque facteur, à déterminer les caractéristiques numériques d’un tel effet, leur fiabilité au moindre coût et dans les meilleurs délais. Résoudre de tels problèmes permet des méthodes d'analyse de la variance.
Analyse à sens unique
L'étude vise à évaluer l'ampleur de l'impact d'un cas particulier sur l'analyse analysée. Une analyse à sens unique peut également consister à comparer deux ou plusieurs circonstances afin de déterminer la différence entre leurs effets sur le rappel. Si l'hypothèse nulle est rejetée, l'étape suivante sera l'évaluation quantitative et la construction d'intervalles de confiance pour les caractéristiques obtenues. Dans le cas où hypothèse nulle ne peut être écarté, il est généralement accepté et une conclusion est tirée sur l'essence de l'influence.
L'analyse de variance univariée peut devenir un analogue non paramétrique de la méthode de Kraskel-Wallis. Il a été développé par le mathématicien américain William Kraskel et l'économiste Wilson Wallis en 1952. Ce critère a été assigné pour tester l'hypothèse nulle selon laquelle les effets sur les échantillons étudiés sont égaux aux valeurs moyennes inconnues mais égales. Le nombre d'échantillons doit être supérieur à deux.

Le critère de Jonkhier (Jonkhier-Terpstra) a été proposé indépendamment par le mathématicien néerlandais T.J. Terpstrom en 1952 et par le psychologue britannique E.R. Jonkhier en 1954. Il est utilisé lorsqu'il est connu à l'avance que les groupes de résultats disponibles sont classés par la croissance de l'influence du facteur étudié, mesurée dans une échelle ordinale.
M - le test de Bartlett, proposé par le statisticien britannique Maurice Stevenson Bartlett en 1937, permet de tester l'hypothèse nulle de l'égalité des variances de plusieurs populations générales normales auxquelles les échantillons étudiés ont été prélevés, ayant généralement des volumes différents (le nombre de chaque échantillon doit être d'au moins quatre). )
G est le test de Cochren, découvert par l’Américain William Gemmel Cochren en 1941. Il permet de tester l’hypothèse nulle selon laquelle les variances des populations générales normales sont égales pour des échantillons indépendants de volume égal.
Le critère non paramétrique de Levene, proposé par le mathématicien américain Howard Levene en 1960, est une alternative au critère de Bartlett dans des conditions où il n’est pas certain que les échantillons étudiés obéissent à la distribution normale.
En 1974, les statisticiens américains Morton B. Brown et Alan B. Forsyth ont proposé un test (critère de Brown-Forsythe), qui diffère quelque peu du critère de Leuven.
Analyse à deux facteurs
L'analyse de variance dans les deux sens est utilisée pour les échantillons couplés normalement distribués. En pratique, on utilise souvent des tableaux complexes de cette méthode, en particulier ceux dans lesquels chaque cellule contient un ensemble de données (mesures répétées) correspondant à des valeurs de niveau fixe. Si les hypothèses nécessaires pour appliquer une analyse de variance bidirectionnelle ne sont pas remplies, le critère de rang non paramétrique de Friedman (Friedman, Kendall et Smith) développé par l'économiste américain Milton Friedman à la fin de 1930 est indépendant du type de distribution.
On suppose seulement que la distribution des quantités est la même et continue, et qu'elles sont indépendantes les unes des autres. Lors du test de l'hypothèse nulle, le résultat est présenté sous la forme d'une matrice rectangulaire dans laquelle les lignes correspondent aux niveaux du facteur B et les colonnes correspondent aux niveaux de A. Chaque cellule du tableau (bloc) peut être le résultat de mesures de paramètres sur un objet ou sur un groupe d'objets à des valeurs constantes des niveaux des deux facteurs . Dans ce cas, les données correspondantes sont fournies en tant que valeurs moyennes d'un certain paramètre pour toutes les mesures ou objets de l'échantillon étudié. Pour appliquer le critère des données de sortie, il est nécessaire de passer des résultats de mesure directs à leur rang. Le classement est effectué pour chaque ligne séparément, c'est-à-dire que les valeurs sont ordonnées pour chaque valeur fixe.

Le critère de page (critère L), proposé par le statisticien américain E. B. Page en 1963, est destiné à tester l'hypothèse nulle. Pour les grands échantillons, l’approximation de page est utilisée. Soumis à la réalité des hypothèses nulles correspondantes, ils obéissent à la distribution normale standard. Dans le cas où les lignes de la table source ont les mêmes valeurs, il est nécessaire d'utiliser des classements moyens. De plus, la précision des conclusions sera d'autant plus mauvaise que plus il y aura de coïncidences.
Q est le critère de Cochren proposé par V. Cohren en 1937. Il est utilisé dans les cas où des groupes de sujets homogènes sont exposés à plus de deux et pour lesquels deux réponses sont possibles - conditionnellement négative (0) et conditionnellement positive (1). . L'hypothèse nulle consiste en des effets d'influence égaux. L'analyse de variance dans les deux sens permet de déterminer l'existence d'effets de traitement, mais ne permet pas d'établir pour quelles colonnes cet effet existe. Pour résoudre ce problème, la méthode des équations multiples de Sheffe pour les échantillons couplés est utilisée.
Analyse multivariée
L'analyse de variance multivariée est une tâche qui se pose lorsqu'il est nécessaire de déterminer l'influence de deux conditions ou plus sur une variable aléatoire donnée. L'étude prévoit la présence d'une variable aléatoire dépendante, mesurée sur l'échelle de différence ou de relations, et de plusieurs variables indépendantes, chacune étant exprimée dans l'échelle des noms ou en rang. L'analyse des données de variance est une section assez développée de la statistique mathématique, qui comporte de nombreuses options. Le concept de recherche est commun aux facteurs simples et multiples. Son essence est que la variance totale est divisée en composants, ce qui correspond à un certain regroupement de données. Chaque groupe de données a son propre modèle.Nous ne considérerons ici que les dispositions de base nécessaires à la compréhension et à l’utilisation pratique des options les plus largement utilisées.
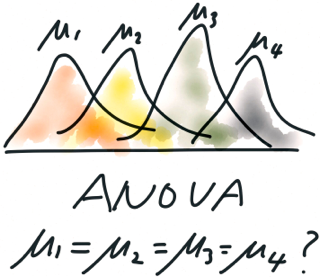
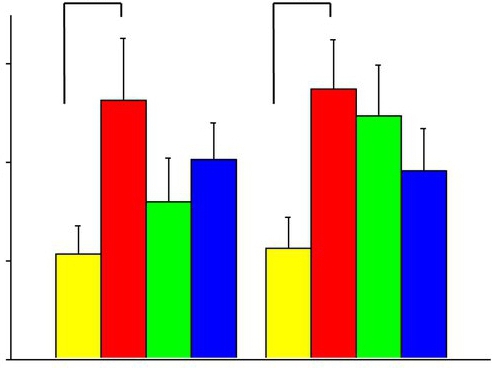
L'analyse de la variance des facteurs nécessite une attitude plutôt prudente vis-à-vis de la collecte et de la présentation des données d'entrée, en particulier de l'interprétation des résultats. Contrairement à un facteur, dont les résultats peuvent être placés arbitrairement dans une certaine séquence, les résultats à deux facteurs nécessitent une représentation plus complexe. Une situation encore plus difficile survient quand il y a trois, quatre ou plus de circonstances. Pour cette raison, plus de trois (quatre) conditions sont rarement incluses dans un modèle. Un exemple est la survenue d'une résonance à une certaine valeur de la capacité et de l'inductance du cercle électrique; la manifestation d'une réaction chimique avec un certain ensemble d'éléments à partir duquel le système est construit; l'apparition d'effets anormaux dans des systèmes complexes avec une certaine coïncidence de circonstances. La présence d'interaction peut modifier fondamentalement le modèle du système et parfois amener à repenser la nature des phénomènes auxquels l'expérimentateur est confronté.
Analyse de variance multivariée avec expériences répétées
Les données de mesure peuvent souvent être regroupées non pas par deux, mais par un plus grand nombre de facteurs. Ainsi, si nous considérons l’analyse de la variance de la durée de vie des pneus des roues du trolleybus en tenant compte des circonstances (le fabricant et l’itinéraire sur lequel les pneus sont exploités), nous pouvons distinguer la saison au cours de laquelle les pneus sont exploités (exploitation hiver et été). En conséquence, nous aurons la tâche d’une méthode à trois facteurs.
S'il y a plus de conditions, l'approche est la même que dans l'analyse à deux facteurs. Dans tous les cas, ils essaient de simplifier le modèle. Le phénomène de l'interaction de deux facteurs ne se manifeste pas si souvent et la triple interaction ne se produit que dans des cas exceptionnels. Ils incluent l'interaction pour laquelle il existe des informations antérieures et de bonnes raisons de la prendre en compte dans le modèle. Le processus consistant à isoler des facteurs individuels et à les prendre en compte est relativement simple. Par conséquent, il y a souvent une volonté de souligner davantage de circonstances. Cela ne devrait pas être emporté. Plus le nombre de conditions est élevé, moins le modèle est fiable et plus la probabilité d'erreur est grande. Le modèle lui-même, qui comprend un grand nombre de variables indépendantes, devient assez difficile à interpréter et peu pratique pour une utilisation pratique.
L'idée générale de l'analyse de variance
L'analyse de la variance dans les statistiques est une méthode permettant d'obtenir les résultats d'observations dépendantes de diverses circonstances existantes simultanément et d'évaluer leur impact. Un facteur contrôlé correspond à une variable contrôlée qui correspond à la méthode permettant d’influencer l’objet de l’étude et d’acquérir une certaine valeur dans un laps de temps donné. Ils peuvent être qualitatifs et quantitatifs. Les niveaux de conditions quantitatives acquièrent une certaine valeur sur une échelle numérique. Les exemples sont la température, la pression, la quantité de substance. Les facteurs qualitatifs sont différentes substances, différentes méthodes technologiques, appareils, charges. Leurs niveaux correspondent à l'échelle des noms.
La qualité peut également inclure le type de matériau d'emballage, les conditions de stockage de la forme posologique. Il est également rationnel d’attribuer le degré de broyage des matières premières, la composition fractionnelle des granules qui ont une importance quantitative, mais qui sont difficiles à contrôler si une échelle quantitative est utilisée. Le nombre de facteurs de qualité dépend du type de forme posologique, ainsi que des propriétés physiques et technologiques des substances médicamenteuses. Par exemple, des comprimés peuvent être obtenus à partir de substances cristallines par compression directe. Dans ce cas, il suffit de faire un choix de substances glissantes et lubrifiantes.
Exemples de facteurs qualitatifs pour divers types de formes posologiques
- Teintures. La composition de l'agent d'extraction, le type d'extracteur, la méthode de préparation des matières premières, la méthode de production, la méthode de filtrage.
- Extraits (liquides, épais, secs). La composition de l'agent d'extraction, la méthode d'extraction, le type d'installation, la méthode d'élimination de l'agent d'extraction et des substances de ballast.
- Pilules La composition des excipients, des charges, des délitants, des liants, des lubrifiants et des agents de glissement. Méthode de production de comprimés, type d'équipement de traitement. Type de coque et ses composants, filmogènes, pigments, colorants, plastifiants, solvants.
- Solutions d'injection. Type de solvant, méthode de filtration, nature des stabilisants et des conservateurs, conditions de stérilisation, méthode de remplissage des ampoules.
- Suppositoires. La composition de la base de suppositoire, une méthode de production de suppositoires, des charges, des emballages.
- Pommades. La composition de la base, les composants structurels, le mode de préparation de la pommade, le type d’équipement, l’emballage.
- Capsules Type de matériau de coque, méthode de fabrication des capsules, type de plastifiant, agent de conservation, colorant.
- Liniment. La méthode de préparation, la composition, le type d’équipement, le type d’émulsifiant.
- Suspensions Type de solvant, type de stabilisant, méthode de dispersion.
Exemples de facteurs qualitatifs et de leurs niveaux étudiés dans le processus de fabrication de comprimés
- Poudre à pâte. Fécule de pomme de terre, argile blanche, mélange de bicarbonate de sodium et d’acide citrique, carbonate de magnésium basique.
- Solution de liant. Eau, pâte d'amidon, sirop de sucre, solution de méthylcellulose, solution d'hydroxypropylméthylcellulose, solution de polyvinylpyrrolidone, solution d'alcool polyvinylique.
- Substance glissante. Aerosil, amidon, talc.
- Remplisseur. Sucre, glucose, lactose, chlorure de sodium, phosphate de calcium.
- Lubrifiant. Acide stéarique, polyéthylène glycol, paraffine.
Analyse des modèles de variance dans l'étude de la compétitivité des états
L'un des critères les plus importants pour évaluer l'état de l'État, ainsi que son niveau de bien-être et son développement socio-économique, est la compétitivité, c'est-à-dire un ensemble de propriétés inhérentes à l'économie nationale qui déterminent la capacité de l'État à faire concurrence aux autres pays. Après avoir déterminé la place et le rôle de l’État sur le marché mondial, nous pouvons établir une stratégie claire pour assurer sécurité économique sur le plan international, car c'est la clé de relations positives entre la Russie et tous les acteurs du marché mondial: investisseurs, créanciers, gouvernements des États.
Pour comparer le niveau de compétitivité des pays, les pays sont classés à l'aide d'indices complexes comprenant divers indicateurs pondérés. La base de ces indices est constituée par les facteurs clés affectant la situation économique, politique, etc. Un ensemble de modèles pour étudier la compétitivité de l'État prévoit l'utilisation de méthodes d'analyse statistique à plusieurs variables (en particulier, l'analyse de la variance (statistique), la modélisation économétrique, la prise de décision) et comprend les principales étapes suivantes:
- Formation d'un système d'indicateurs-indicateurs.
- Évaluation et prévision des indicateurs de la compétitivité des États.
- Comparaison des indicateurs-indicateurs de la compétitivité des États.
Considérons maintenant le contenu des modèles de chacune des étapes de ce complexe.
Dans la première étape À l'aide de méthodes d'étude d'experts, un ensemble justifié d'indicateurs économiques-indicateurs d'évaluation de la compétitivité de l'État est formé, prenant en compte les spécificités de son développement sur la base des notations internationales et des données des services statistiques reflétant l'état du système dans son ensemble et de ses processus.Le choix de ces indicateurs est justifié par la nécessité de sélectionner ceux qui, du point de vue de la pratique, permettent le plus de déterminer le niveau de l’État, son attractivité pour les investissements et les possibilités de localisation relative des menaces potentielles et réelles existantes.
Les principaux indicateurs-indicateurs des systèmes de notation internationaux sont les indices:
- Compétitivité globale (IGC).
- Liberté économique (IES).
- Développement humain (HDI).
- Perceptions de la corruption (CPI).
- Menaces internes et externes.
- Le potentiel d'influence internationale (IPMV).
Deuxième étape Il prévoit l’évaluation et la prévision d’indicateurs de la compétitivité des États en fonction des notations internationales attribuées aux 139 pays du monde étudiés.
Troisième étape fournit une comparaison des conditions de compétitivité des états en utilisant des méthodes analyse de corrélation et de régression.
En utilisant les résultats de l’étude, il est possible de déterminer la nature des processus dans leur ensemble et par des composantes individuelles de la compétitivité de l’État; tester l'hypothèse de l'influence des facteurs et de leur relation avec les facteurs appropriés niveau de signification.
La mise en œuvre de la série de modèles proposée permettra non seulement d’évaluer la situation actuelle du niveau de compétitivité et d’attractivité des investissements des États, mais également d’analyser les faiblesses de la gestion, de prévenir les erreurs de décision erronées et de prévenir le développement d’une crise dans l’État.



