Dans l'article, nous examinerons le concept de "probabilité d'un événement accidentel". On sait que dans divers domaines de l'activité humaine, il existe des phénomènes impossibles à prédire avec précision. Ainsi, par exemple, le volume des ventes de produits dépend à la fois des besoins très changeants des clients et d'autres nuances qu'il est impossible de prendre en compte. C'est pourquoi, en créant de la production et en réalisant des ventes, les propriétaires doivent prévoir le résultat de leurs activités sur la base de leur expérience personnelle ou des compétences similaires d'autres personnes.
Pour évaluer l'événement en question, il est nécessaire de prendre en compte ou de créer spécialement les conditions dans lesquelles il est enregistré. De telles actions sont appelées expérience ou expérience. Dans son processus, il y a des épisodes possibles qui sont appelés aléatoires, si à la fin ils peuvent avoir lieu ou non, ainsi que des phénomènes fiables qui résultent de la pratique.
Nous étudions la probabilité d'un événement à l'aide d'exemples. Par exemple, la chute de neige à Moscou le 25 novembre est considérée comme un épisode aléatoire. Le lever du soleil au quotidien est un phénomène fiable, et les chutes de neige à l'équateur sont considérées comme une curiosité impossible. L'une des tâches les plus importantes de la théorie des probabilités est le problème de la détermination d'une mesure quantitative de la possibilité qu'un événement se produise.
Probabilité
La probabilité est le degré (évaluation quantitative, mesure relative) de la possibilité de survenue d'un événement. Lorsque des arguments opposés l'emportent sur les raisons pour lesquelles un événement éventuel est en réalité compensé, ce cas est appelé probable. Sinon, cela s'appelle douteux ou incroyable.
La prépondérance de la base négative sur la base positive, et inversement, peut être à des degrés divers, en raison desquels l'irrecevabilité (ou l'admissibilité) est moindre ou plus grande. Pour cette raison, la probabilité d'un événement est souvent perçue à un niveau de première classe, en particulier dans les passages où il est extrêmement difficile, voire impossible, de donner une évaluation quantitative précise. Bien entendu, différentes gradations de niveaux de chance sont possibles.
Analyse de probabilité
À propos, la probabilité d’événements indépendants a des paramètres spéciaux. Et rechercher une chance dans une position mathématique complète une discipline spécifique - la théorie des probabilités. Dans cet enseignement et cette statistique mathématique, le concept d'admissibilité est officialisé comme une description numérique de l'épisode (une mesure probabiliste ou sa signification).
En fait, il s’agit d’une mesure sur de nombreux cas (sous-ensembles de nombreux phénomènes élémentaires), acquérant des valeurs de 0 à 1:
- une valeur de 1 correspond à un épisode valide;
- un fait impossible a une chance nulle (l'inverse est presque toujours faux).
Si l'occurrence du phénomène est p, alors le risque d'inertie est 1-p. Disons que probabilité ½ signifie la même possibilité d'occurrence et de non-occurrence du cas.

Déclaration de hasard
Test, événement, probabilité - ces variables sont étroitement liées à la science. Une définition typique du hasard repose sur la notion d'équiprobabilité des résultats.
Le rapport entre le nombre de finales contribuant à cet événement et le nombre total de fins tout aussi possibles est une opportunité. Par exemple, l’admissibilité d’une «queue» ou d’un «aigle» s’éclate si un lancer non intentionnel d’un sou est de 1/2, si l’on calcule que seuls ces deux chemins sont également probables.

Cette définition classique du hasard peut être généralisée au cas d'un nombre inépuisable de valeurs potentielles.Par exemple, si un phénomène peut se produire avec la même admissibilité en un point quelconque (le nombre de points est illimité) d'une région locale du plan (espace), le risque qu'il se produise dans une certaine partie de cette sphère acceptable correspond au rapport de la surface (volume) de cette partie à la zone (volume) de la zone de tous les points possibles.
Lien
La probabilité d'un événement peut être déterminée de manière empirique. Cela est dû à la fréquence d'apparition de l'épisode basée sur le fait qu'avec un nombre impressionnant de tests, la fréquence devrait poursuivre un degré objectif de possibilité de ce précédent.
Dans la présentation actuelle de la théorie des probabilités, le hasard se révèle de manière axiomatique, en tant que fait particulier de la théorie abstraite de la mesure d'un ensemble. Cependant, entre la recevabilité exprimant le degré de réalité de l'occurrence du phénomène et la mesure abstraite, le lien est précisément la fréquence de son suivi.

Bien entendu, la probabilité d'occurrence d'un événement dans divers processus est possible. Une interprétation stochastique de certains phénomènes est largement répandue dans la science moderne, en particulier en économétrie, en physique statistique des systèmes thermodynamiques (visibles), où même dans le cas d’une description classique déterministe du mouvement des particules, une description concrète de toute leur structure ne semble ni pratique ni possible. En physique quantique, les processus caractérisés eux-mêmes ont une nature stochastique.
Événement aléatoire
Bien entendu, la probabilité d'occurrence d'un événement dans chaque processus non contrôlé est élevée. Qu'est-ce qu'une contingence? Ceci est un sous-ensemble des nombreux résultats d'une expérience accidentelle. Si une enquête aléatoire est répétée plusieurs fois, la fréquence d'occurrence d'un fait sert à évaluer son admissibilité. 
Un phénomène involontaire qui ne se produit jamais à la suite d'une expérience involontaire est appelé impossible. Un épisode aléatoire, qui est toujours réalisé à la suite d'une expérience inattendue, est appelé fiable. Et comment caractérise-t-on la probabilité d'événements indépendants? On sait que deux faits aléatoires sont qualifiés d’indépendants si l’apparition de l’un d’eux ne change pas l’admissibilité de l’apparence de l’autre.
Un événement aléatoire est un événement régulier créé en générant des fonctions involontaires avec substitution de variables aléatoires à des variables. La fonction ordinaire de génération d'un numéro de loterie est réalisée par des outils informatiques.
La définition
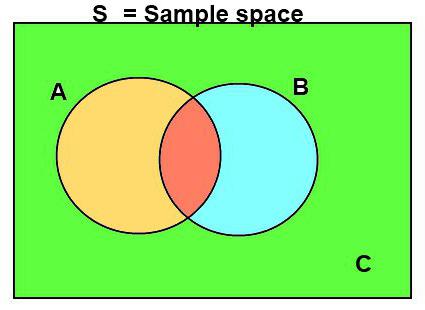
Un épisode mathématiquement aléatoire est un sous-ensemble de l'espace des résultats élémentaires d'un essai non volontaire. C'est un élément de sigma-algèbre ou algèbre - F, qui est lui-même défini de manière évidente et, avec l'espace des phénomènes les plus simples "Omega" et la probabilité P forme un espace de probabilité.
Contexte de la notion de hasard
La probabilité d'un événement accidentel a souvent été étudiée. En général, l’émergence du concept de hasard a toujours été associée au jeu, en particulier aux dés. Avant l’émergence de ce concept, les tâches combinatoires consistant à calculer le nombre de résultats potentiels lors du lancement d’une paire de dés étaient principalement décrites, ainsi que la question de la répartition des paris entre les participants lorsque le jeu se terminait à l’avance.
L'évêque Vibold de la ville de Cambrai en 960 décida le premier rébus en lançant trois dés. Il a compté 56 espèces. Cependant, ce nombre ne reproduit en fait pas la somme des méthodes également possibles, car chacune de leurs 56 versions peut être réalisée avec un nombre de réceptions différent.
La probabilité d'un événement accidentel a été étudiée par Richard de Fornival dans la première moitié du XIIIe siècle. Malgré le fait qu'il mentionne également le nombre 56, il se dit que le même nombre de points sur trois os peut être obtenu par six méthodes.
Sur la base de son raisonnement, il est déjà possible d’établir que le nombre d’options également accessibles est de 216. Par la suite, beaucoup n’ont pas résolu ce problème correctement.Pour la première fois, Gallileo Galilei a calculé le nombre de résultats tout aussi accessibles lors du lancement de trois os: il a élevé les six (nombre de versions de la perte d'un os) au degré 3 (le nombre d'os). Il a également compilé un tableau du nombre d'options pour extraire différentes quantités de points.
Nous espérons que notre article vous familiarise avec la probabilité d’un événement aléatoire.








