Корелационен и регресионен анализ: пример, задачи, приложение. Метод на корелационен и регресионен анализ

Корелационен регресионен анализ - Това е един от най-разпространените методи за изследване на връзката между числовите стойности. Основната му цел е да се намери връзката между двата параметъра и степента му с последващо извеждане на уравнението. Например имаме ученици, издържали изпита по математика и английски език. Можем да използваме корелация, за да определим дали успехът на един тест влияе на резултатите в друг предмет. Що се отнася до регресионния анализ, той помага да се прогнозират математическите оценки въз основа на точките, получени в изпит по английски език, и обратно.

Какво представлява корелационната диаграма?

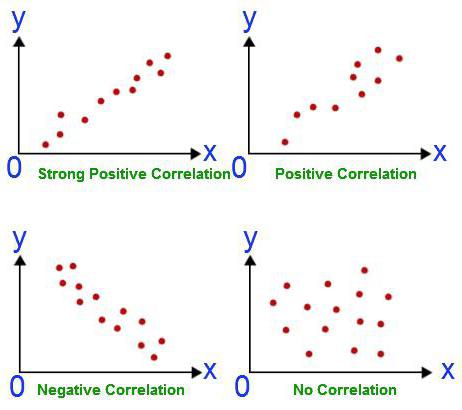
Всеки анализ започва със събирането на информация. Колкото повече е, толкова по-точно се получава резултатът в крайна сметка. В горния пример имаме две дисциплини, в които студентите трябва да положат изпит. Степента на техния успех е оценка. Корелационно-регресионен анализ показва дали резултатът от един предмет влияе на точките, получени във втория изпит. За да се отговори на този въпрос, е необходимо да се анализират паралелно оценките на всички студенти. Но първо трябва да вземете решение за зависимата променлива. В този случай не е толкова важно. Да предположим, че изпитът по математика се е състоял по-рано. Точките върху него са независима променлива (те се отлагат по абсцисата). Английският е в разписанието по-късно. Следователно оценките, базирани на него, са зависима променлива (нанасят се по протежение на ординатата). Колкото повече получената графика изглежда като права линия, толкова по-силна е линейната корелация между двете избрани стойности. Това означава, че учениците по математика са по-склонни да получат петици на изпита по английски език.

Предположения и опростявания

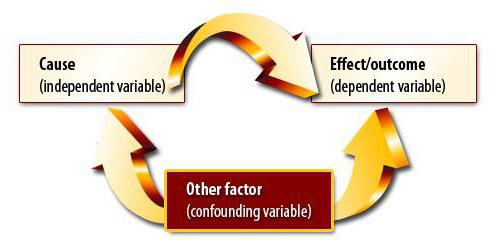
Методът на корелационен и регресионен анализ включва намиране на причинно-следствена връзка. На първия етап обаче трябва да разберете, че промените в двете количества могат да се дължат на някаква трета, която все още не е взета предвид от изследователя. Между променливите може да има и нелинейни отношения, следователно получаването на коефициент, равен на нула, не е краят на експеримента.

Линейна корелация на Пиърсън

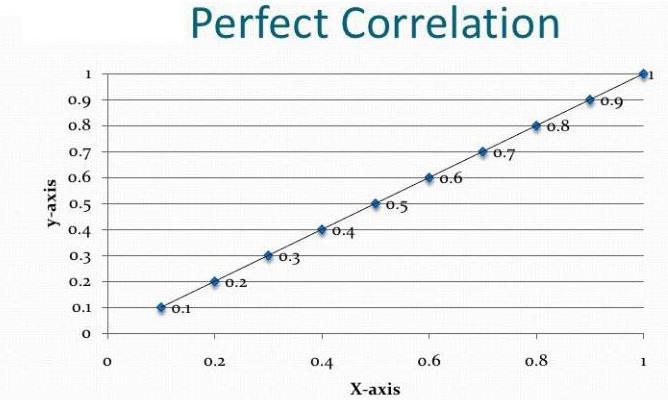
Този коефициент може да се използва при две условия. Първият - всички стойности на променливите са рационални числа, вторият - очаква се стойностите да се променят пропорционално. Този коефициент винаги е между -1 и 1. Ако е по-голям от нула, тогава има пряко пропорционална зависимост, по-малка - обратно, равна - тези стойности не влияят една върху друга по никакъв начин. Възможността за изчисляване на този показател е в основата на корелационния и регресионен анализ. За първи път този коефициент е разработен от Карл Пиърсън въз основа на идеята на Франсис Галтън.

Свойства и предпазни мерки

Коефициентът на корелация на Пиърсън е мощен инструмент, но той също трябва да се използва с повишено внимание. Следните предупреждения са в употреба:

1. Коефициентът на Пирсън показва наличието или отсъствието на линейна връзка. Корелационно-регресионният анализ не свършва дотук, може да се окаже, че променливите все пак са взаимосвързани.
2. Човек трябва да бъде внимателен при интерпретиране на стойността на коефициента. Може да се намери корелация между размера на краката и нивото на IQ.Но това не означава, че един индикатор определя друг.
3. Коефициентът на Пирсън не казва нищо за причинно-следствената връзка между показателите.

Коефициент на корелация на Спирман

Ако промяна в стойността на един показател води до увеличаване или намаляване на стойността на друг, това означава, че те са свързани. Корелационно-регресионен анализ, пример за който ще бъде даден по-долу, е точно свързан с такива параметри. Ранков коефициент ви позволява да опростите изчисленията.

Корелационен и регресионен анализ: пример

Да предположим, че има оценка на ефективността на десет предприятия. Имаме двама съдии, които им дават точки. В този случай корелационният и регресионен анализ на предприятието не може да се извърши въз основа на линеен коефициент на Пиърсън. Не се интересуваме от връзката между оценките на съдиите. Важни са редиците на предприятията според съдиите.

Този вид анализ има следните предимства:

• Непараметрична форма на отношенията между изследваните величини.
• Лесна употреба, тъй като ранговете могат да бъдат приписани както във възходящ, така и по низходящ ред.

Единственото изискване на този тип анализи е необходимостта от конвертиране на изходните данни.

Проблеми с приложението

Корелационният и регресионен анализ се основава на следните предположения:

• Наблюденията се считат за независими (петкратната загуба на „орела“ не влияе на резултата от следващия флип на монетата).
• В корелационния анализ и двете променливи се считат за случайни. При регресия - само един (зависим).
• При тестване на хипотеза трябва да се спазва нормално разпределение. Промяната в зависимата променлива трябва да бъде еднаква за всяка стойност на абсцисата.
• Корелационната диаграма е само първият тест на хипотезата за връзката между двете серии параметри, а не и крайният резултат от анализа.

Зависимост и причинно-следствена връзка

Да предположим, че сме изчислили коефициента на корелация на обема на износа и БВП. Оказа се равен на модул на единство. Правихме ли корелационен и регресионен анализ докрай? Разбира се, че не. Полученият резултат изобщо не означава, че БВП може да се изрази чрез износ. Все още не сме доказали причинно-следствената връзка между показателите. Корелационно-регресионен анализ - прогнозиране на стойностите на една променлива въз основа на друга. Трябва обаче да разберете, че често много фактори влияят върху параметъра. Износът определя БВП, но не само той. Има и други фактори. Тук има връзка и причинно-следствена връзка, макар и коригирана за други компоненти на брутния вътрешен продукт.

Друга ситуация е много по-опасна. Във Великобритания беше проведено проучване, което показа, че децата, чиито родители са пушили, са по-често нарушители. Този извод се основава на силна зависимост между показателя. Но правилен ли е? Първо, зависимостта може да бъде обратна. Родителите биха могли да започнат да пушат поради стрес от факта, че децата им постоянно влизат в промени и нарушават закона. Второ, и двата параметъра може да се дължат на третия. Такива семейства принадлежат към ниските социални класове, които се характеризират и от двата проблема. Следователно въз основа на корелацията не може да се заключи, че има причинно-следствена връзка.

Защо да използвате регресионен анализ?

Корелационната зависимост включва намиране на връзки между количествата. Причинно-следствената връзка в този случай остава зад кулисите. Задачите на корелационния и регресионен анализ съвпадат само по отношение на потвърждаване на съществуването на връзка между стойностите на две величини. Първоначално изследователят обаче не обръща внимание на възможността за причинно-следствена връзка. Регресионният анализ винаги има две променливи, едната от които зависи. Провежда се на няколко етапа:

1. Избор на подходящ модел, използвайки метода на най-малко квадратчета.
2. Извличане на уравнение, описващо ефекта от промяна на независима променлива върху друга.

Например, ако изучаваме ефекта на възрастта върху човешкия растеж, тогава регресионният анализ може да помогне за прогнозиране на промените през годините.

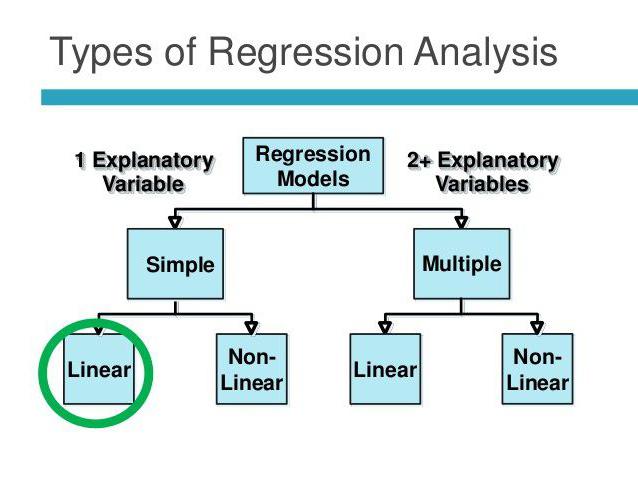
Линейна и множествена регресия

Да предположим, че X и Y са две свързани променливи. Регресионният анализ ни позволява да прогнозираме величината на единия от тях въз основа на стойностите на другия. Например, зрялостта и възрастта са зависими симптоми. Връзката между тях се отразява с помощта на линейна регресия. Всъщност можете да изразите X чрез Y или обратно. Но често само една от регресионните линии е правилна. Успехът на анализа до голяма степен зависи от правилното определяне на независимата променлива. Например имаме два показателя: добив и валежи. От ежедневния опит става ясно, че първото зависи от второто, а не обратното.

Множествената регресия ви позволява да изчислите неизвестна стойност въз основа на стойностите на три или повече променливи. Например добивът на ориз на декар земя зависи от качеството на зърното, плодородието на почвата, торовете, температурата и валежите. Всички тези параметри влияят на общия резултат. За опростяване на модела се използват следните предположения:

• Връзката между независимите и влияещите характеристики е линейна.
• Мултиколинеарността е изключена. Това означава, че зависимите променливи не са свързани помежду си.
• Хомоскедастичност и нормалност на серии от числа.

Използването на корелационен и регресионен анализ

Има три основни случая на използване на този метод:

1. Тестване на случайни връзки между количества. В този случай изследователят определя стойностите на променливата и установява дали те влияят върху промяната в зависимата променлива. Например, можете да давате на хората различни дози алкохол и да измервате тяхното кръвно налягане. В този случай изследователят знае със сигурност, че първото е причината за второто, а не обратното. Корелационно-регресионен анализ ви позволява да откриете пряко пропорционална линейна връзка между тези две променливи и да извлечете формула, която я описва. В този случай стойностите, изразени в напълно различни мерни единици, могат да бъдат сравнени.
2. Намиране на връзка между две променливи, без да се разширява причинно-следствената връзка към тях. В този случай няма разлика какъв размер изследователят нарича зависим. Освен това в действителност може да се окаже, че и двамата са засегнати от третата променлива, следователно те се променят пропорционално.
3. Изчисляване на стойностите на едно количество въз основа на друго. Той се основава на уравнение, в което са заместени известни числа.

По този начин, корелационният анализ включва намиране на връзка (не причинно-следствена) между променливите, а регресионният анализ го обяснява, често използвайки математическа функция.