Регресионният анализ е статистически метод за изследване на зависимостта на случайна променлива от променливи

При статистическо моделиране регресионният анализ е проучване, използвано за оценка на връзката между променливите. Този математически метод включва много други методи за моделиране и анализ на няколко променливи, когато акцентът е върху връзката между зависимата променлива и една или повече независими. По-конкретно, регресионният анализ помага да се разбере как типичната стойност на зависима променлива се променя, ако една от независимите променливи се промени, докато другите независими променливи остават фиксирани.

Във всички случаи целевата оценка е функция на независими променливи и се нарича функция на регресия. При регресионен анализ също е интересно да се характеризира промяната в зависимата променлива като функция на регресията, която може да бъде описана с помощта на разпределение на вероятността.

Задачи за регресионен анализ

Този метод на статистически изследвания се използва широко за прогнозиране, където използването му има значително предимство, но понякога може да доведе до илюзии или фалшиви връзки, поради което се препоръчва внимателно да се използва в този брой, защото например корелацията не означава причинно-следствена връзка.

Разработен е голям брой методи за провеждане на регресионен анализ, като линейна и обикновена регресия с най-малки квадрати, които са параметрични. Тяхната същност е, че регресионната функция се дефинира по отношение на ограничен брой неизвестни параметри, които се изчисляват от данните. Непараметричната регресия позволява функциите му да лежат в определен набор от функции, които могат да бъдат безгранични.

Като метод на статистически изследвания, регресионният анализ на практика зависи от формата на процеса на генериране на данни и от това как е свързан с регресионния подход. Тъй като истинската форма на процеса на данни генерира като правило неизвестно число, регресионният анализ на данните често до известна степен зависи от предположенията за този процес. Тези предположения понякога се проверяват, ако има достатъчно данни. Регресионните модели често са полезни, дори когато предположенията са умерено нарушени, въпреки че не могат да работят с максимална ефективност.

В по-тесен смисъл, регресията може да се отнася конкретно за оценката на променливите на непрекъснат отговор, за разлика от променливите на дискретен отговор, използвани в класификацията. Случаят на непрекъсната изходна променлива се нарича също метрична регресия, за да се разграничи от свързаните с нея проблеми.

Историята

Най-ранната форма на регресия е добре известният метод на най-малките квадрати. Той е публикуван от Legendre през 1805 г. и Gauss през 1809 г. Legendre и Gauss прилагат метода за задачата да определят от астрономически наблюдения орбитите на телата около Слънцето (главно комети, но по-късно новооткрити малки планети). През 1821 г. Гаус публикува допълнително развитие на теорията за най-малките квадрати, включително версия на теоремата на Гаус-Марков.

Терминът „регресия“ е въведен от Франсис Галтън през 19 век, за да опише биологичен феномен. Изводът беше, че растежът на потомците от растежа на предците, като правило, намалява до нормалната средна стойност.За Галтън регресията има само това биологично значение, но по-късно работата му е продължена от Удни Юл и Карл Пиърсън и е доведена до по-общ статистически контекст. В работата на Юл и Пиърсън съвместното разпределение на променливите на отговора и обяснителните променливи се счита за Гаус. Това предположение е отхвърлено от Фишър в творбите от 1922 и 1925 година. Фишър предположи, че условното разпределение на променливата на отговора е Гаус, но съвместното разпределение не трябва да бъде. В това отношение предположението на Фишер е по-близо до формулировката на Гаус от 1821 г. До 1970 г. понякога са били необходими до 24 часа, за да се получи резултат от регресионен анализ.

Методите за регресионен анализ продължават да бъдат област на активното изследване. През последните десетилетия бяха разработени нови методи за надеждна регресия; регресия, включваща корелиращи отговори; регресионни методи, приспособяващи различни видове липсващи данни; непараметрична регресия; Байесовски регресионен метод; регресии, при които променливите на прогнозата се измерват с грешка; регресии с повече предиктори, отколкото наблюдения, както и причинно-следствени изводи с регресия.

Регресионни модели

Моделите за регресионен анализ включват следните променливи:

• Неизвестни параметри, обозначени като бета, които могат да бъдат скаларни или векторни.
• Независими променливи, X.
• Зависими променливи, Y.

В различни области на науката, където се прилага регресионен анализ, се използват различни термини вместо зависими и независими променливи, но във всички случаи регресионният модел се отнася Y към функциите X и β.

Приближаването обикновено има формата E (Y | X) = F (X, β). За да се проведе регресионен анализ, трябва да се определи вида на функцията f. По-рядко той се основава на знания за връзката между Y и X, които не разчитат на данни. Ако такива знания не са налични, тогава се избира гъвкава или удобна форма F.

Зависима променлива Y

Сега нека предположим, че векторът с неизвестни параметри β има дължина k. За да извърши регресионен анализ, потребителят трябва да предостави информация за зависимата променлива Y:

• Ако има N точки от данни от формата (Y, X), където N

• Ако се наблюдава точно N = K и функцията F е линейна, тогава уравнението Y = F (X, β) може да бъде решено точно, а не приблизително. Това се свежда до решаване на набор от N-уравнения с N-неизвестни (елементи на β), който има уникално решение, стига X да е линейно независим. Ако F е нелинеен, решението може да не съществува или може да има много решения.
• Най-често срещаната е ситуацията, при която се наблюдават N> точки към данните. В този случай има достатъчно информация в данните, за да се оцени уникалната стойност на β, която най-добре съвпада с данните, и регресионният модел, когато се прилага към данните, може да се счита за преразпределена система в β.

В последния случай регресионният анализ предоставя инструменти за:

• Намиране на решения за неизвестни параметри β, които например ще сведат до минимум разстоянието между измерените и прогнозираните стойности на Y.
• При определени статистически предположения регресионният анализ използва излишната информация, за да предостави статистическа информация за неизвестни параметри β и прогнозираните стойности на зависимата променлива Y.

Необходим брой независими измервания

Помислете за регресионен модел, който има три неизвестни параметъра: β₀, β₁ и β₂, Да предположим, че експериментаторът извършва 10 измервания в една и съща стойност на независимата променлива на вектора X.В този случай регресионният анализ не дава уникален набор от стойности. Най-доброто, което можете да направите, е да оцените средното и стандартното отклонение на зависимата променлива Y. Чрез измерване на две различни стойности на X по един и същи начин, можете да получите достатъчно данни за регресия с две неизвестни, но не и за три или повече неизвестни.

Ако измерванията на експериментатора са извършени при три различни стойности на независимата променлива на вектора X, тогава регресионният анализ ще предостави уникален набор от оценки за три неизвестни параметъра в β.

В случай на обща линейна регресия, горното твърдение е еквивалентно на изискването, че матрицата X^TX е обратим.

Статистически предположения

Когато броят на измерванията N е по-голям от броя на неизвестните параметри k и грешката на измерване ε_аз, като правило, излишъкът от информация, съдържаща се в измерванията, след това се разпределя и използва за статистически прогнози относно неизвестни параметри. Този излишък от информация се нарича степен на свобода на регресия.

Фундаментални предположения

Класическите предположения за регресионен анализ включват:

• Пробата е представителна за прогнозиране на изводите.
• Грешката е случайна променлива със средна стойност нула, която е обусловена от обяснителните променливи.
• Независимите променливи се измерват без грешка.
• Като независими променливи (предиктори) те са линейно независими, тоест не е възможно да се изрази какъвто и да е предиктор под формата на линейна комбинация от останалите.
• Грешките са некорелирани, т.е. ковариационната матрица на диагоналните грешки и всеки ненулев елемент са вариацията на грешката.
• Вариантът на грешката е постоянен според наблюденията (хомосекедастичност). Ако не, можете да използвате метода с най-малко претеглени квадрати или други методи.

Тези достатъчни условия за оценка на най-малките квадрати притежават необходимите свойства, по-специално тези предположения означават, че оценките на параметрите ще бъдат обективни, последователни и ефективни, особено когато се вземат предвид в класа на линейни оценки. Важно е да се отбележи, че доказателствата рядко отговарят на условията. Тоест методът се използва, дори ако предположенията не са верни. Разнообразие от предположения понякога може да се използва като мярка за това колко полезен е този модел. Много от тези предположения могат да бъдат смекчени чрез по-модерни методи. Отчетите за статистически анализ обикновено включват анализ на тестове, базирани на извадкови данни и методология за полезност на модела.

В допълнение, променливите в някои случаи се отнасят до стойности, измерени на точкови места. Възможно е да има пространствени тенденции и пространствена автокорелация в променливи, които нарушават статистическите предположения. Географската претеглена регресия е единственият метод, който се занимава с такива данни.

Линеен регресионен анализ

При линейна регресия характеристика е, че зависимата променлива, която е Y_азе линейна комбинация от параметри. Например, в обикновена линейна регресия, една независима променлива, x, се използва за моделиране на n-точки_аз, и два параметъра, β₀ и β₁.

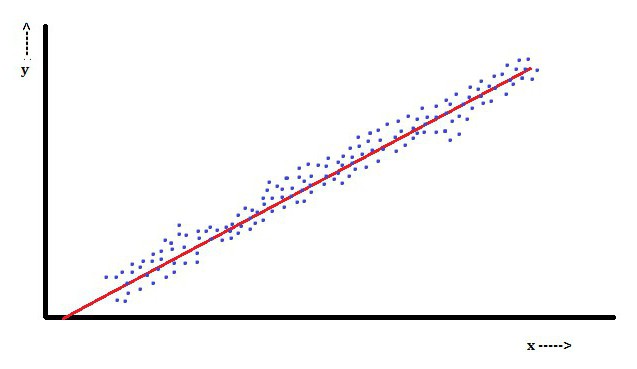
При множествена линейна регресия има няколко независими променливи или техните функции.

С произволна извадка от популация, нейните параметри позволяват да се получи пример за линеен регресионен модел.

В този аспект най-популярен е методът с най-малко квадратчета. Използвайки го, се получават оценки на параметрите, които свеждат до минимум сумата от квадратни остатъци. Този вид минимизиране (което е характерно за линейна регресия) на тази функция води до набор от нормални уравнения и набор от линейни уравнения с параметри, които са решени за получаване на оценки на параметрите.

При по-нататъшното предположение, че грешката в популацията обикновено се разпространява, изследователят може да използва тези оценки на стандартни грешки, за да създаде интервали на доверие и да тества хипотези за неговите параметри.

Нелинеен регресионен анализ

Пример, при който функцията не е линейна по отношение на параметрите, показва, че сборът на квадратите трябва да се сведе до минимум с помощта на итеративна процедура. Това въвежда много усложнения, които определят разликите между линейните и нелинейните методи на най-малките квадрати. Следователно, резултатите от регресионния анализ, използвайки нелинейния метод, понякога са непредсказуеми.

Изчисляване на мощността и размера на пробата

Тук като правило няма последователни методи по отношение на броя на наблюденията в сравнение с броя на независимите променливи в модела. Първото правило е предложено от Good and Hardin и изглежда като N = t ^ n, където N е размерът на извадката, n е броят на независимите променливи и t е броят на наблюденията, необходими за постигане на желаната точност, ако моделът има само една независима променлива. Например, изследовател изгражда линеен регресионен модел, използвайки набор от данни, който съдържа 1000 пациенти (N). Ако изследователят реши, че са необходими пет наблюдения, за да се определи точно линията (m), тогава максималният брой независими променливи, които моделът може да поддържа, е 4.

Други методи

Въпреки факта, че параметрите на регресионния модел обикновено се оценяват по метода на най-малките квадрати, има и други методи, които се използват много по-рядко. Например, това са следните методи:

• Байесови методи (напр. Байесов метод на линейна регресия).
• Процентна регресия, използвана за ситуации, когато намалението на процентните грешки се счита за по-подходящо.
• Най-малките абсолютни отклонения, които са по-стабилни при наличието на външни вещества, водещи до квантилна регресия.
• Непараметрична регресия, изискваща голям брой наблюдения и изчисления.
• Разстоянието на метриката за учене, което се изучава в търсене на значително метрично разстояние в дадено входно пространство.

софтуер

Всички основни статистически софтуерни пакети се извършват, като се използва регресионен анализ с най-малко квадрати. Простата линейна регресия и множествен регресионен анализ могат да се използват в някои приложения за електронни таблици, както и в някои калкулатори. Въпреки че много статистически софтуерни пакети могат да извършват различни видове непараметрична и надеждна регресия, тези методи са по-малко стандартизирани; различни софтуерни пакети прилагат различни методи. Разработен е специализиран регресионен софтуер за използване в области като анализ на изследване и невровизуализация.