Ανάλυση Αντίστροφης Συσχέτισης - Αυτή είναι μια από τις πιο κοινές μεθόδους για τη μελέτη της σχέσης μεταξύ αριθμητικών τιμών. Ο κύριος στόχος του είναι να βρει τη σχέση μεταξύ των δύο παραμέτρων και το βαθμό του με την επακόλουθη παραγωγή της εξίσωσης. Για παράδειγμα, έχουμε φοιτητές που έχουν περάσει τις μαθηματικές και αγγλικές εξετάσεις. Μπορούμε να χρησιμοποιήσουμε συσχετισμό για να καθορίσουμε αν η επιτυχία μιας δοκιμής επηρεάζει τα αποτελέσματα σε ένα άλλο θέμα. Όσον αφορά την ανάλυση παλινδρόμησης, βοηθά στην πρόβλεψη βαθμών μαθηματικών με βάση τα σημεία που βαθμολογούνται σε μια αγγλική εξέταση και αντίστροφα.

Τι είναι ένας πίνακας συσχετισμού;
Κάθε ανάλυση αρχίζει με τη συλλογή πληροφοριών. Όσο περισσότερο είναι, τόσο πιο ακριβές είναι το αποτέλεσμα που έχει επιτευχθεί στο τέλος. Στο παραπάνω παράδειγμα, έχουμε δύο κλάδους στις οποίες οι φοιτητές πρέπει να περάσουν μια εξέταση. Το ποσοστό επιτυχίας τους είναι μια εκτίμηση. Η ανάλυση συσχέτισης-παλινδρόμησης δείχνει αν το αποτέλεσμα ενός υποκειμένου επηρεάζει τους βαθμούς που σημειώθηκαν στη δεύτερη εξέταση. Προκειμένου να δοθεί απάντηση σε αυτή την ερώτηση, είναι απαραίτητο να αναλυθούν οι αξιολογήσεις όλων των φοιτητών παράλληλα. Αλλά πρώτα πρέπει να αποφασίσετε για την εξαρτημένη μεταβλητή. Σε αυτή την περίπτωση, δεν είναι τόσο σημαντικό. Ας υποθέσουμε ότι μια εξέταση μαθηματικών πραγματοποιήθηκε νωρίτερα. Τα σημεία σε αυτό είναι μια ανεξάρτητη μεταβλητή (αναβάλλεται κατά μήκος της τετμημένης). Τα αγγλικά βρίσκονται στο πρόγραμμα αργότερα. Επομένως, οι εκτιμήσεις που βασίζονται σε αυτό είναι μια εξαρτημένη μεταβλητή (σχεδιάζονται κατά μήκος της τεταγμένης). Όσο περισσότερο το γράφημα που προκύπτει έτσι μοιάζει με ευθεία γραμμή, τόσο ισχυρότερη είναι η γραμμική συσχέτιση μεταξύ των δύο επιλεγμένων τιμών. Αυτό σημαίνει ότι οι μαθητές στα μαθηματικά είναι πιο πιθανό να πάρουν πέντε βαθμούς στην αγγλική εξέταση.
Υποθέσεις και Απλοποιήσεις
Η μέθοδος της συσχέτισης και της ανάλυσης παλινδρόμησης περιλαμβάνει την εύρεση μιας αιτιώδους σχέσης. Ωστόσο, στο πρώτο στάδιο, θα πρέπει να καταλάβετε ότι οι αλλαγές και στις δύο ποσότητες μπορεί να οφείλονται σε μερικές τρίτες, οι οποίες δεν έχουν ακόμη ληφθεί υπόψη από τον ερευνητή. Μπορούν επίσης να υπάρχουν μη γραμμικές σχέσεις μεταξύ των μεταβλητών, επομένως, η λήψη ενός συντελεστή ίσης με το μηδέν δεν είναι το τέλος του πειράματος.
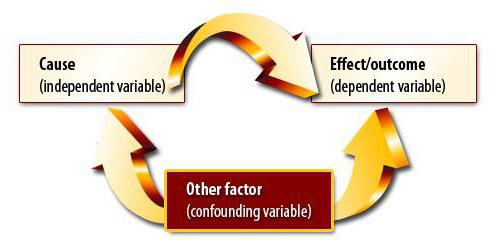
Pearson γραμμική συσχέτιση
Αυτός ο συντελεστής μπορεί να χρησιμοποιηθεί υπό δύο προϋποθέσεις. Η πρώτη - όλες οι τιμές των μεταβλητών είναι λογικοί αριθμοί, ο δεύτερος - αναμένεται ότι οι τιμές αλλάζουν αναλογικά. Αυτός ο συντελεστής είναι πάντοτε μεταξύ -1 και 1. Αν είναι μεγαλύτερο από το μηδέν, τότε υπάρχει μια άμεση αναλογική εξάρτηση, λιγότερο - αντίστροφα, ίση - αυτές οι τιμές δεν επηρεάζουν ο ένας τον άλλο με κανέναν τρόπο. Η ικανότητα υπολογισμού αυτού του δείκτη είναι η βάση της ανάλυσης συσχέτισης και παλινδρόμησης. Για πρώτη φορά, ο συντελεστής αυτός αναπτύχθηκε από τον Karl Pearson με βάση την ιδέα του Francis Galton.
Ιδιότητες και προφυλάξεις
Ο συντελεστής συσχέτισης του Pearson είναι ένα ισχυρό εργαλείο, αλλά πρέπει επίσης να χρησιμοποιείται με προσοχή. Οι παρακάτω προειδοποιήσεις είναι στη χρήση του:
- Ο συντελεστής Pearson υποδηλώνει την παρουσία ή την απουσία μιας γραμμικής σχέσης. Η ανάλυση συσχέτισης-παλινδρόμησης δεν τελειώνει εκεί, μπορεί να αποδειχθεί ότι οι μεταβλητές αλληλοσυνδέονται.
- Κάποιος πρέπει να είναι προσεκτικός στην ερμηνεία της τιμής του συντελεστή. Υπάρχει συσχέτιση μεταξύ του μεγέθους του ποδιού και του επιπέδου IQ.Αλλά αυτό δεν σημαίνει ότι ένας δείκτης καθορίζει άλλο.
- Ο συντελεστής Pearson δεν λέει τίποτα για την αιτιώδη σχέση μεταξύ των δεικτών.

Συγκριτικός συντελεστής συσχέτισης του Spearman
Εάν μια αλλαγή στην τιμή ενός δείκτη οδηγεί σε αύξηση ή μείωση της αξίας ενός άλλου, τότε αυτό σημαίνει ότι είναι σχετικές. Η ανάλυση συσχέτισης-παλινδρόμησης, ένα παράδειγμα της οποίας θα δοθεί παρακάτω, συνδέεται επακριβώς με τέτοιες παραμέτρους. Ο συντελεστής κατάταξης σας επιτρέπει να απλοποιήσετε τους υπολογισμούς.
Ανάλυση συσχετισμού και παλινδρόμησης: ένα παράδειγμα
Ας υποθέσουμε ότι υπάρχει αξιολόγηση της αποτελεσματικότητας των δέκα επιχειρήσεων. Έχουμε δύο δικαστές που τους δίνουν τα σημεία. Η ανάλυση συσχέτισης και παλινδρόμησης της επιχείρησης στην περίπτωση αυτή δεν μπορεί να πραγματοποιηθεί με βάση τον γραμμικό συντελεστή Pearson. Δεν μας ενδιαφέρει η σχέση μεταξύ των αξιολογήσεων των δικαστών. Οι βαθμοί των επιχειρήσεων σύμφωνα με τους δικαστές είναι σημαντικοί.
Αυτός ο τύπος ανάλυσης έχει τα ακόλουθα πλεονεκτήματα:
- Μη-παραμετρική μορφή σχέσεων μεταξύ των ποσοτήτων που μελετήθηκαν.
- Εύκολη χρήση, επειδή οι τάξεις μπορούν να αποδοθούν τόσο σε αύξουσα σειρά αξίας όσο και σε φθίνουσα σειρά.
Η μόνη απαίτηση αυτού του τύπου ανάλυσης είναι η ανάγκη μετατροπής των δεδομένων προέλευσης.
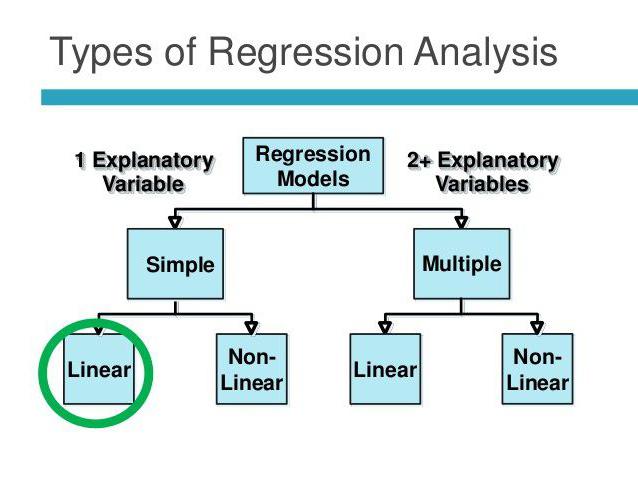
Προβλήματα εφαρμογής
Η ανάλυση συσχέτισης και παλινδρόμησης βασίζεται στις ακόλουθες παραδοχές:
- Οι παρατηρήσεις θεωρούνται ανεξάρτητες (πενταπλάσια απώλεια του "αετού" δεν επηρεάζει το αποτέλεσμα του επόμενου flip νομίσματος).
- Στην ανάλυση συσχέτισης, και οι δύο μεταβλητές θεωρούνται τυχαίες. Στην παλινδρόμηση - μόνο μία (εξαρτώμενη).
- Κατά τη δοκιμή μιας υπόθεσης πρέπει να τηρείται κανονική κατανομή. Η μεταβολή της εξαρτώμενης μεταβλητής πρέπει να είναι η ίδια για κάθε τιμή στην τετμημένη.
- Το διάγραμμα συσχέτισης είναι μόνο η πρώτη δοκιμή της υπόθεσης σχετικά με τη σχέση μεταξύ των δύο σειρών παραμέτρων και όχι το τελικό αποτέλεσμα της ανάλυσης.
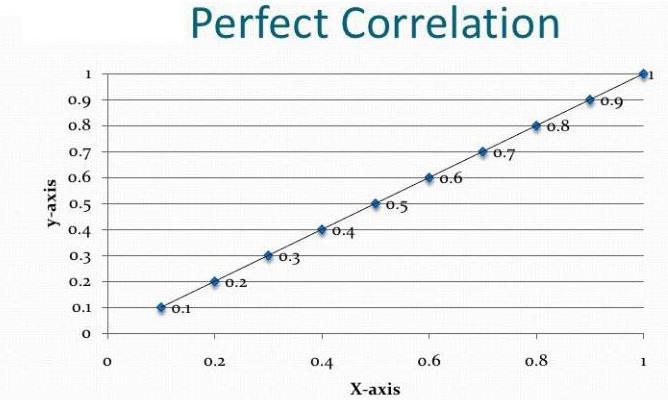
Εξάρτηση και αιτιώδης συνάφεια
Ας υποθέσουμε ότι υπολογίσαμε τον συντελεστή συσχέτισης του όγκου των εξαγωγών και του ΑΕΠ. Αποδείχθηκε ότι είναι ίσο με το modulo ενότητας. Έχουμε κάνει την ανάλυση συσχέτισης και παλινδρόμησης στο τέλος; Φυσικά όχι. Το αποτέλεσμα που προκύπτει δεν σημαίνει ότι το ΑΕΠ μπορεί να εκφραστεί μέσω εξαγωγών. Δεν έχουμε ακόμη αποδείξει την αιτιώδη συνάφεια μεταξύ των δεικτών. Ανάλυση συσχέτισης-παλινδρόμησης - πρόβλεψη των τιμών μιας μεταβλητής που βασίζεται σε άλλη. Ωστόσο, πρέπει να καταλάβετε ότι συχνά επηρεάζουν την παράμετρο πολλούς παράγοντες. Η εξαγωγή καθορίζει το ΑΕγχΠ, αλλά όχι μόνο αυτό. Υπάρχουν και άλλοι παράγοντες. Εδώ υπάρχει μια συσχέτιση και μια αιτιώδης σχέση, αν και προσαρμόζεται για άλλα στοιχεία του ακαθάριστου εγχώριου προϊόντος.
Μια άλλη κατάσταση είναι πολύ πιο επικίνδυνη. Στο Ηνωμένο Βασίλειο, διεξήχθη έρευνα που έδειξε ότι τα παιδιά των οποίων οι γονείς καπνίζουν ήταν πιο συχνά παραβάτες. Το συμπέρασμα αυτό βασίζεται σε ισχυρή συσχέτιση μεταξύ του δείκτη. Αλλά είναι σωστός; Πρώτον, η εξάρτηση μπορεί να είναι αντίστροφη. Οι γονείς θα μπορούσαν να ξεκινήσουν το κάπνισμα εξ αιτίας του γεγονότος ότι τα παιδιά τους συνεχώς μεταβάλλονται και παραβιάζουν το νόμο. Δεύτερον, και οι δύο παράμετροι μπορεί να οφείλονται στην τρίτη. Τέτοιες οικογένειες ανήκουν σε χαμηλές κοινωνικές τάξεις, οι οποίες χαρακτηρίζονται από αμφότερα τα προβλήματα. Συνεπώς, με βάση τη συσχέτιση, δεν μπορεί να συναχθεί το συμπέρασμα ότι υπάρχει μια αιτιώδης σχέση.
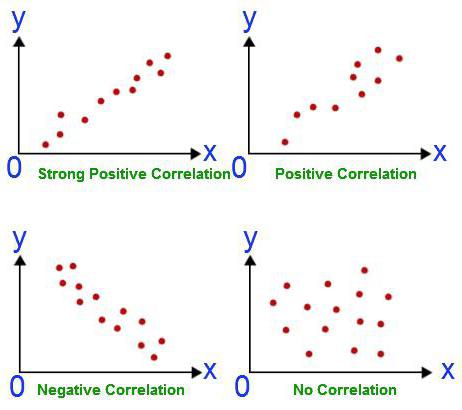
Γιατί να χρησιμοποιήσετε την ανάλυση παλινδρόμησης;
Η εξάρτηση της συσχέτισης συνεπάγεται εύρεση σχέσεων μεταξύ των ποσοτήτων. Η αιτιώδης σχέση σε αυτή την περίπτωση παραμένει στα παρασκήνια. Τα καθήκοντα της ανάλυσης συσχέτισης και παλινδρόμησης συμπίπτουν μόνο με την επιβεβαίωση της ύπαρξης σχέσης μεταξύ των αξιών δύο ποσοτήτων. Ωστόσο, αρχικά ο ερευνητής δεν δίνει προσοχή στη δυνατότητα μιας αιτιώδους σχέσης. Η ανάλυση παλινδρόμησης έχει πάντα δύο μεταβλητές, μία από τις οποίες εξαρτάται. Πραγματοποιείται σε διάφορα στάδια:
- Επιλέγοντας το σωστό μοντέλο με τη μέθοδο των ελάχιστων τετραγώνων.
- Παράγωγο μιας εξίσωσης που περιγράφει το αποτέλεσμα μιας αλλαγής σε μια ανεξάρτητη μεταβλητή σε μια άλλη.
Για παράδειγμα, αν μελετήσουμε την επίδραση της ηλικίας στην ανθρώπινη ανάπτυξη, τότε μια ανάλυση παλινδρόμησης μπορεί να βοηθήσει στην πρόβλεψη αλλαγών κατά τη διάρκεια των ετών.
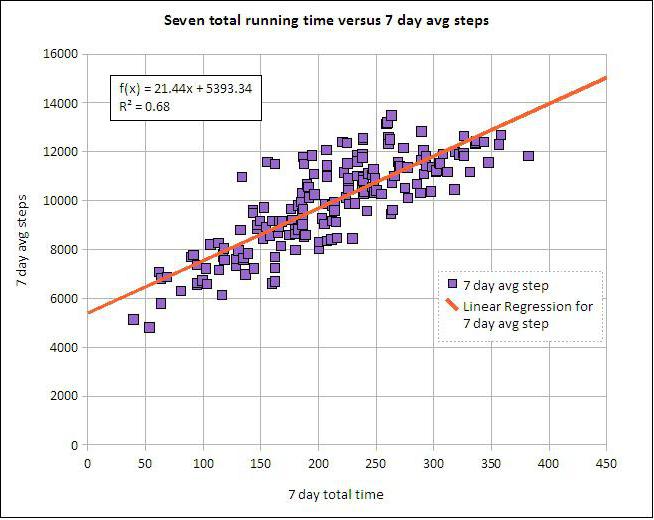
Γραμμική και πολλαπλή παλινδρόμηση
Ας υποθέσουμε ότι X και Y είναι δύο σχετικές μεταβλητές. Η ανάλυση της παλινδρόμησης μας επιτρέπει να προβλέπουμε το μέγεθος ενός από αυτά με βάση τις αξίες του άλλου. Για παράδειγμα, η ωριμότητα και η ηλικία είναι εξαρτώμενα συμπτώματα. Η σχέση μεταξύ τους αντικατοπτρίζεται χρησιμοποιώντας γραμμική παλινδρόμηση. Στην πραγματικότητα, μπορείτε να εκφράσετε το Χ μέσω του Y ή το αντίστροφο. Αλλά συχνά μόνο μία από τις γραμμές παλινδρόμησης είναι σωστή. Η επιτυχία της ανάλυσης εξαρτάται σε μεγάλο βαθμό από τον σωστό προσδιορισμό της ανεξάρτητης μεταβλητής. Για παράδειγμα, έχουμε δύο δείκτες: απόδοση και βροχόπτωση. Από την καθημερινή εμπειρία, γίνεται σαφές ότι η πρώτη εξαρτάται από τη δεύτερη και όχι το αντίστροφο.
Η πολλαπλή παλινδρόμηση σάς επιτρέπει να υπολογίσετε μια άγνωστη τιμή που βασίζεται στις τιμές τριών ή περισσοτέρων μεταβλητών. Για παράδειγμα, η απόδοση του ρυζιού ανά στρέμμα γης εξαρτάται από την ποιότητα των σιτηρών, τη γονιμότητα του εδάφους, τα λιπάσματα, τη θερμοκρασία και τις βροχοπτώσεις. Όλες αυτές οι παράμετροι επηρεάζουν το συνολικό αποτέλεσμα. Για την απλοποίηση του μοντέλου, χρησιμοποιούνται οι παρακάτω υποθέσεις:
- Η σχέση μεταξύ ανεξάρτητων και επηρεαστικών χαρακτηριστικών είναι γραμμική.
- Η πολυελαστικότητα αποκλείεται. Αυτό σημαίνει ότι οι εξαρτημένες μεταβλητές δεν αλληλοσυνδέονται.
- Homoskedasticity και κανονικότητα σειράς αριθμών.
Η χρήση ανάλυσης συσχετισμού και παλινδρόμησης
Υπάρχουν τρεις κύριες περιπτώσεις χρήσης αυτής της μεθόδου:
- Δοκιμάζοντας τυχαίες σχέσεις μεταξύ των ποσοτήτων. Σε αυτή την περίπτωση, ο ερευνητής καθορίζει τις τιμές της μεταβλητής και διαπιστώνει εάν επηρεάζει τη μεταβολή της εξαρτώμενης μεταβλητής. Για παράδειγμα, μπορείτε να δώσετε στους ανθρώπους διαφορετικές δόσεις αλκοόλ και να μετρήσετε την αρτηριακή τους πίεση. Σε αυτή την περίπτωση, ο ερευνητής γνωρίζει με βεβαιότητα ότι η πρώτη είναι η αιτία του δεύτερου και όχι το αντίστροφο. Η ανάλυση αντιστοίχισης-παλινδρόμησης σάς επιτρέπει να ανιχνεύσετε μια άμεση αναλογική γραμμική σχέση μεταξύ αυτών των δύο μεταβλητών και να αντλήσετε έναν τύπο που την περιγράφει. Στην περίπτωση αυτή, οι τιμές που εκφράζονται σε εντελώς διαφορετικές μονάδες μέτρησης μπορούν να συγκριθούν.
- Εύρεση σχέσης μεταξύ δύο μεταβλητών χωρίς να επεκτείνεται μια αιτιώδης σχέση με αυτές. Σε αυτήν την περίπτωση, δεν υπάρχει διαφορά σε ποιο μέγεθος ο ερευνητής καλεί εξαρτώμενο. Επιπλέον, στην πραγματικότητα, μπορεί να αποδειχθεί ότι και οι δύο επηρεάζονται από την τρίτη μεταβλητή, επομένως αλλάζουν αναλογικά.
- Υπολογισμός τιμών μίας ποσότητας βάσει άλλου. Βασίζεται σε μια εξίσωση στην οποία οι γνωστοί αριθμοί αντικαθίστανται.
Έτσι, η ανάλυση συσχέτισης περιλαμβάνει την εύρεση μιας σύνδεσης (όχι αιτιώδους) μεταξύ μεταβλητών, και η ανάλυση παλινδρόμησης εξηγεί αυτό, συχνά χρησιμοποιώντας μια μαθηματική συνάρτηση.








