Η ανάλυση παλινδρόμησης είναι μια στατιστική μέθοδος για τη μελέτη της εξάρτησης μιας τυχαίας μεταβλητής από τις μεταβλητές

Στη στατιστική μοντελοποίηση, η ανάλυση παλινδρόμησης είναι μια μελέτη που χρησιμοποιείται για την αξιολόγηση της σχέσης μεταξύ μεταβλητών. Αυτή η μαθηματική μέθοδος περιλαμβάνει πολλές άλλες μεθόδους για μοντελοποίηση και ανάλυση πολλών μεταβλητών, όταν η εστίαση είναι στη σχέση μεταξύ της εξαρτημένης μεταβλητής και μιας ή περισσότερων ανεξάρτητων. Ειδικότερα, η ανάλυση παλινδρόμησης συμβάλλει στην κατανόηση του τρόπου αλλαγής μιας τυπικής τιμής μιας εξαρτημένης μεταβλητής, εάν αλλάξει μία από τις ανεξάρτητες μεταβλητές, ενώ οι άλλες ανεξάρτητες μεταβλητές παραμένουν σταθερές.

Σε όλες τις περιπτώσεις, η εκτίμηση του στόχου είναι συνάρτηση των ανεξάρτητων μεταβλητών και ονομάζεται συνάρτηση παλινδρόμησης. Στην ανάλυση παλινδρόμησης, είναι επίσης ενδιαφέρον να χαρακτηρίσουμε τη μεταβολή της εξαρτώμενης μεταβλητής ως συνάρτηση της παλινδρόμησης, η οποία μπορεί να περιγραφεί χρησιμοποιώντας μια κατανομή πιθανότητας.

Εργασίες ανάλυσης παλινδρόμησης

Αυτή η μέθοδος στατιστικής έρευνας χρησιμοποιείται ευρέως για την πρόβλεψη, όπου η χρήση της έχει ένα σημαντικό πλεονέκτημα, αλλά μερικές φορές μπορεί να οδηγήσει σε ψευδαισθήσεις ή ψευδείς σχέσεις, επομένως συνιστάται να τη χρησιμοποιήσετε προσεκτικά σε αυτό το ζήτημα, διότι, για παράδειγμα, η συσχέτιση δεν σημαίνει αιτιώδη συνάφεια.

Ένας μεγάλος αριθμός μεθόδων έχει αναπτυχθεί για τη διεξαγωγή ανάλυσης παλινδρόμησης, όπως η γραμμική και η συνηθισμένη παλινδρόμηση των ελαχίστων τετραγώνων, οι οποίες είναι παραμετρικές. Η ουσία τους είναι ότι η συνάρτηση παλινδρόμησης ορίζεται από έναν πεπερασμένο αριθμό άγνωστων παραμέτρων που εκτιμώνται από τα δεδομένα. Η μη παραμετρική παλινδρόμηση επιτρέπει στις λειτουργίες της να βρίσκονται σε ένα ορισμένο σύνολο λειτουργιών, οι οποίες μπορεί να είναι άπειρες.

Ως μέθοδος στατιστικής έρευνας, η ανάλυση παλινδρόμησης στην πράξη εξαρτάται από τη μορφή της διαδικασίας παραγωγής δεδομένων και από τον τρόπο που σχετίζεται με την προσέγγιση παλινδρόμησης. Δεδομένου ότι η πραγματική μορφή της διαδικασίας των δεδομένων παράγει, κατά κανόνα, έναν άγνωστο αριθμό, η ανάλυση παλινδρόμησης των δεδομένων εξαρτάται συχνά σε κάποιο βαθμό από τις υποθέσεις σχετικά με αυτή τη διαδικασία. Αυτές οι υποθέσεις ελέγχονται μερικές φορές εάν υπάρχουν αρκετά διαθέσιμα δεδομένα. Τα μοντέλα παλινδρόμησης είναι συχνά χρήσιμα ακόμα και όταν οι παραδοχές παραβιάζονται μέτρια, αν και δεν μπορούν να λειτουργήσουν με τη μέγιστη απόδοση.

Σε μια στενότερη έννοια, η παλινδρόμηση μπορεί να αφορά ειδικά την εκτίμηση των μεταβλητών συνεχούς απόκρισης, σε αντίθεση με τις διακριτές μεταβλητές απόκρισης που χρησιμοποιούνται στην ταξινόμηση. Η περίπτωση μίας μεταβλητής συνεχούς εξόδου ονομάζεται επίσης μετρική παλινδρόμηση προκειμένου να διακριθεί από τα σχετικά προβλήματα.

Η ιστορία

Η παλαιότερη μορφή της παλινδρόμησης είναι η γνωστή μέθοδος ελαχίστων τετραγώνων. Δημοσιεύτηκε από τον Legendre το 1805 και από τον Gauss το 1809. Ο Legendre και ο Gauss εφάρμοσαν τη μέθοδο στο πρόβλημα του προσδιορισμού από αστρονομικές παρατηρήσεις των τροχιών γύρω από τον ήλιο (κυρίως κομήτες, αλλά αργότερα ανακάλυψαν μικρούς πλανήτες). Ο Gauss δημοσίευσε μια περαιτέρω ανάπτυξη της θεωρίας των ελαχίστων τετραγώνων το 1821, συμπεριλαμβανομένης μιας έκδοσης του θεωρήματος Gauss-Markov.

Ο όρος "παλινδρόμηση" σχεδιάστηκε από τον Francis Galton τον 19ο αιώνα για να περιγράψει ένα βιολογικό φαινόμενο. Η κατώτατη γραμμή ήταν ότι η ανάπτυξη των απογόνων από την ανάπτυξη των προγόνων, κατά κανόνα, μειώνεται στο κανονικό μέσο όρο.Για τον Galton, η παλινδρόμηση είχε μόνο αυτό το βιολογικό νόημα, αλλά αργότερα το έργο του συνεχίστηκε από τους Udney Yule και Karl Pearson και έφερε σε ένα γενικότερο στατιστικό πλαίσιο. Στο έργο του Yule και Pearson, η κοινή κατανομή των μεταβλητών απόκρισης και επεξηγηματικών μεταβλητών θεωρείται Gaussian. Αυτή η υπόθεση απορρίφθηκε από τον Fisher στα έργα του 1922 και του 1925. Ο Fisher πρότεινε ότι η εξαρτώμενη κατανομή της μεταβλητής απόκρισης είναι Gaussian, αλλά η κοινή κατανομή δεν πρέπει να είναι. Από αυτή την άποψη, η υπόθεση του Fischer είναι πιο κοντά στη διατύπωση Gauss του 1821. Μέχρι το 1970, κάποτε χρειάστηκε έως και 24 ώρες για να πάρει το αποτέλεσμα μιας ανάλυσης παλινδρόμησης.

Οι μέθοδοι ανάλυσης της παλινδρόμησης συνεχίζουν να αποτελούν τομέα ενεργητικής έρευνας. Τις τελευταίες δεκαετίες έχουν αναπτυχθεί νέες μέθοδοι για την αξιόπιστη παλινδρόμηση. παλινδρόμηση που περιλαμβάνει συσχετισμένες απαντήσεις. μέθοδοι παλινδρόμησης που εξυπηρετούν διάφορους τύπους δεδομένων που λείπουν · μη παραμετρική παλινδρόμηση. Bayesian μέθοδοι παλινδρόμησης; παλινδρομήσεις στις οποίες οι μεταβλητές πρόβλεψης μετρούνται με ένα σφάλμα. παλινδρομήσεις με περισσότερους προγνωστικούς παράγοντες από τις παρατηρήσεις, καθώς και αιτιώδη συμπεράσματα με παλινδρόμηση.

Μοντέλα παλινδρόμησης

Τα μοντέλα ανάλυσης παλινδρόμησης περιλαμβάνουν τις ακόλουθες μεταβλητές:

• Άγνωστες παράμετροι, χαρακτηρισμένες ως beta, οι οποίες μπορεί να είναι κλιμακωτές ή διανυσματικές.
• Ανεξάρτητες μεταβλητές, Χ.
• Εξαρτημένες μεταβλητές, Y.

Σε διάφορους τομείς της επιστήμης όπου εφαρμόζεται ανάλυση παλινδρόμησης, χρησιμοποιούνται διάφοροι όροι αντί για εξαρτώμενες και ανεξάρτητες μεταβλητές, αλλά σε όλες τις περιπτώσεις το μοντέλο παλινδρόμησης σχετίζεται με τις λειτουργίες X και β.

Η προσέγγιση παίρνει συνήθως τη μορφή E (Y | X) = F (X, β). Για να εκτελέσετε μια ανάλυση παλινδρόμησης, πρέπει να προσδιοριστεί ο τύπος της συνάρτησης f. Λιγότερο συχνά, βασίζεται στη γνώση της σχέσης μεταξύ Υ και Χ που δεν βασίζονται σε δεδομένα. Εάν δεν είναι διαθέσιμες αυτές οι γνώσεις, επιλέγεται μια ευέλικτη ή βολική μορφή F.

Εξαρτώμενη μεταβλητή Y

Υποθέστε τώρα ότι ο φορέας άγνωστων παραμέτρων β έχει μήκος k. Για να εκτελέσετε μια ανάλυση παλινδρόμησης, ο χρήστης πρέπει να παράσχει πληροφορίες σχετικά με τη εξαρτημένη μεταβλητή Y:

• Αν υπάρχουν N σημεία δεδομένων της φόρμας (Y, X), όπου N

• Αν παρατηρηθεί ακριβώς N = K και η συνάρτηση F είναι γραμμική, τότε η εξίσωση Y = F (X, β) μπορεί να λυθεί ακριβώς και όχι περίπου. Αυτό μειώνει την επίλυση ενός συνόλου Ν-εξισώσεων με N-unknowns (στοιχεία του β), που έχει μια μοναδική λύση όσο το Χ είναι γραμμικά ανεξάρτητο. Εάν το F είναι μη γραμμικό, η λύση μπορεί να μην υπάρχει ή μπορεί να υπάρχουν πολλές λύσεις.
• Η πιο συνηθισμένη είναι η κατάσταση κατά την οποία τα N> επισημαίνουν τα δεδομένα. Σε αυτή την περίπτωση, υπάρχουν αρκετά στοιχεία στα δεδομένα για να αξιολογηθεί η μοναδική τιμή β που ταιριάζει καλύτερα με τα δεδομένα και το μοντέλο παλινδρόμησης, όταν εφαρμόζεται στα δεδομένα, μπορεί να θεωρηθεί ως ένα υπερπροσδιορισμένο σύστημα στο β.

Στην τελευταία περίπτωση, η ανάλυση παλινδρόμησης παρέχει εργαλεία για:

• Εύρεση λύσεων για άγνωστες παραμέτρους β, οι οποίες θα ελαχιστοποιήσουν, για παράδειγμα, την απόσταση μεταξύ των μετρηθεισών και των προβλεπόμενων τιμών του Y.
• Σύμφωνα με ορισμένες στατιστικές υποθέσεις, η ανάλυση παλινδρόμησης χρησιμοποιεί περίσσεια πληροφοριών για την παροχή στατιστικών πληροφοριών σχετικά με άγνωστες παραμέτρους β και τις προβλεπόμενες τιμές της εξαρτημένης μεταβλητής Y.

Απαραίτητος αριθμός ανεξάρτητων μετρήσεων

Εξετάστε ένα μοντέλο παλινδρόμησης που έχει τρεις άγνωστες παραμέτρους: β₀, β₁ και β₂. Ας υποθέσουμε ότι ο πειραματιστής εκτελεί 10 μετρήσεις στην ίδια τιμή της ανεξάρτητης μεταβλητής του διανύσματος Χ.Στην περίπτωση αυτή, η ανάλυση παλινδρόμησης δεν παρέχει ένα μοναδικό σύνολο τιμών. Το καλύτερο που μπορείτε να κάνετε είναι να αξιολογήσετε τη μέση και τυπική απόκλιση της εξαρτώμενης μεταβλητής Y. Μέτρωντας δύο διαφορετικές τιμές X με τον ίδιο τρόπο, μπορείτε να πάρετε αρκετά δεδομένα για μια παλινδρόμηση με δύο άγνωστα, αλλά όχι για τρία ή περισσότερα άγνωστα.

Εάν οι μετρήσεις του πειραματιστή πραγματοποιήθηκαν σε τρεις διαφορετικές τιμές της ανεξάρτητης μεταβλητής του διανύσματος Χ, τότε η ανάλυση παλινδρόμησης θα παράσχει ένα μοναδικό σύνολο εκτιμήσεων για τρεις άγνωστες παραμέτρους στο β.

Στην περίπτωση της γενικής γραμμικής παλινδρόμησης, η παραπάνω δήλωση ισοδυναμεί με την απαίτηση ότι η μήτρα Χ^ΤΤο X είναι αναστρέψιμο.

Στατιστικές υποθέσεις

Όταν ο αριθμός των μετρήσεων N είναι μεγαλύτερος από τον αριθμό των άγνωστων παραμέτρων k και το σφάλμα μέτρησης ε_i, τότε, κατά κανόνα, η περίσσεια των πληροφοριών που περιέχονται στις μετρήσεις κατανέμεται στη συνέχεια και χρησιμοποιείται για στατιστικές προβλέψεις σχετικά με άγνωστες παραμέτρους. Αυτή η υπερβολική πληροφορία ονομάζεται βαθμός ελευθερίας παλινδρόμησης.

Θεμελιώδεις υποθέσεις

Οι κλασσικές υποθέσεις για την ανάλυση παλινδρόμησης περιλαμβάνουν:

• Το δείγμα είναι αντιπροσωπευτικό της πρόβλεψης των συμπερασμάτων.
• Το σφάλμα είναι μια τυχαία μεταβλητή με μέση τιμή μηδέν, η οποία εξαρτάται από τις επεξηγηματικές μεταβλητές.
• Οι ανεξάρτητες μεταβλητές μετρώνται χωρίς σφάλμα.
• Ως ανεξάρτητες μεταβλητές (predictors), είναι γραμμικές ανεξάρτητες, δηλαδή, δεν είναι δυνατόν να εκφραστεί οποιοσδήποτε προγνωστικός τύπος με τη μορφή ενός γραμμικού συνδυασμού των άλλων.
• Τα σφάλματα δεν είναι συσχετισμένα, δηλ. Η μήτρα συνδιακύμανσης των διαγώνων σφαλμάτων και κάθε μη-φυσικό στοιχείο είναι η διακύμανση του σφάλματος.
• Η διακύμανση του σφάλματος είναι σταθερή σύμφωνα με τις παρατηρήσεις (ομοσκεδαστικότητα). Αν όχι, μπορείτε να χρησιμοποιήσετε τη μέθοδο σταθμισμένων ελαχίστων τετραγώνων ή άλλες μεθόδους.

Αυτές οι επαρκείς συνθήκες για την εκτίμηση των ελάχιστων τετραγώνων έχουν τις απαιτούμενες ιδιότητες, και συγκεκριμένα αυτές οι υποθέσεις σημαίνουν ότι οι εκτιμήσεις των παραμέτρων θα είναι αντικειμενικές, συνεπείς και αποτελεσματικές, ιδίως όταν λαμβάνονται υπόψη στην κατηγορία των γραμμικών εκτιμήσεων. Είναι σημαντικό να σημειωθεί ότι τα στοιχεία σπάνια πληρούν τις προϋποθέσεις. Δηλαδή, η μέθοδος χρησιμοποιείται ακόμη και αν οι υποθέσεις δεν είναι αληθείς. Μια παραλλαγή των υποθέσεων μπορεί μερικές φορές να χρησιμοποιηθεί ως μέτρο για το πόσο χρήσιμο είναι αυτό το μοντέλο. Πολλές από αυτές τις υποθέσεις μπορούν να μετριαστούν με πιο προηγμένες μεθόδους. Οι αναφορές στατιστικής ανάλυσης περιλαμβάνουν συνήθως ανάλυση των δοκιμών που βασίζονται σε δείγματα δεδομένων και μεθοδολογία για τη χρησιμότητα του μοντέλου.

Επιπλέον, οι μεταβλητές σε ορισμένες περιπτώσεις αναφέρονται σε τιμές που μετρήθηκαν σε σημεία σημείου. Μπορεί να υπάρχουν χωρικές τάσεις και χωρική αυτοσυσχέτιση σε μεταβλητές που παραβιάζουν τις στατιστικές υποθέσεις. Η γεωγραφική σταθμισμένη παλινδρόμηση είναι η μόνη μέθοδος που ασχολείται με τέτοια δεδομένα.

Ανάλυση γραμμικής παλινδρόμησης

Σε γραμμική παλινδρόμηση, ένα χαρακτηριστικό είναι ότι η εξαρτημένη μεταβλητή, η οποία είναι Υ_iείναι ένας γραμμικός συνδυασμός παραμέτρων. Για παράδειγμα, σε μια απλή γραμμική παλινδρόμηση, μια ανεξάρτητη μεταβλητή, x, χρησιμοποιείται για να μοντελοποιήσει n-σημεία_i, και δύο παραμέτρους, β₀ και β₁.

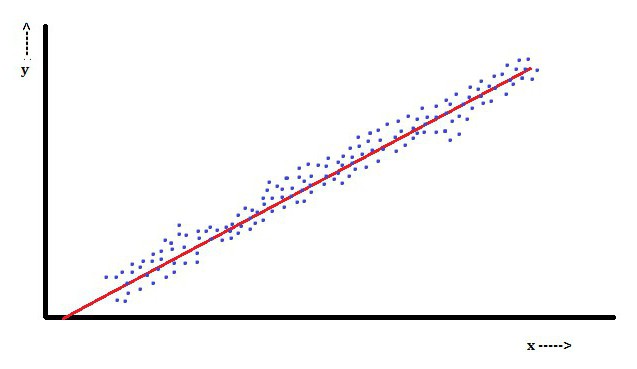
Με πολλαπλή γραμμική παλινδρόμηση, υπάρχουν πολλές ανεξάρτητες μεταβλητές ή οι λειτουργίες τους.

Με τυχαία δειγματοληψία από πληθυσμό, οι παράμετροί του καθιστούν δυνατή την απόκτηση ενός παραδείγματος ενός μοντέλου γραμμικής παλινδρόμησης.

Από αυτή την άποψη, η λιγότερο τετραγωνική μέθοδος είναι η πιο δημοφιλής. Με τη χρήση του, λαμβάνονται εκτιμήσεις παραμέτρων που ελαχιστοποιούν το άθροισμα τετραγωνικών υπολειμμάτων. Αυτός ο τύπος ελαχιστοποίησης (ο οποίος είναι χαρακτηριστικός της γραμμικής παλινδρόμησης) αυτής της συνάρτησης οδηγεί σε ένα σύνολο κανονικών εξισώσεων και σε ένα σύνολο γραμμικών εξισώσεων με παραμέτρους που επιλύονται για να ληφθούν εκτιμήσεις παραμέτρων.

Με την περαιτέρω υπόθεση ότι το σφάλμα του πληθυσμού συνήθως εξαπλώνεται, ο ερευνητής μπορεί να χρησιμοποιήσει αυτές τις εκτιμήσεις τυποποιημένων σφαλμάτων για να δημιουργήσει διαστήματα εμπιστοσύνης και να δοκιμάσει υποθέσεις σχετικά με τις παραμέτρους του.

Ανάλυση μη γραμμικής παλινδρόμησης

Ένα παράδειγμα όπου η συνάρτηση δεν είναι γραμμική σε σχέση με τις παραμέτρους υποδεικνύει ότι το άθροισμα των τετραγώνων πρέπει να ελαχιστοποιείται χρησιμοποιώντας μια επαναληπτική διαδικασία. Αυτό εισάγει πολλές επιπλοκές που καθορίζουν τις διαφορές μεταξύ γραμμικών και μη γραμμικών μεθόδων ελαχίστων τετραγώνων. Συνεπώς, τα αποτελέσματα της ανάλυσης παλινδρόμησης χρησιμοποιώντας τη μη γραμμική μέθοδο είναι μερικές φορές απρόβλεπτες.

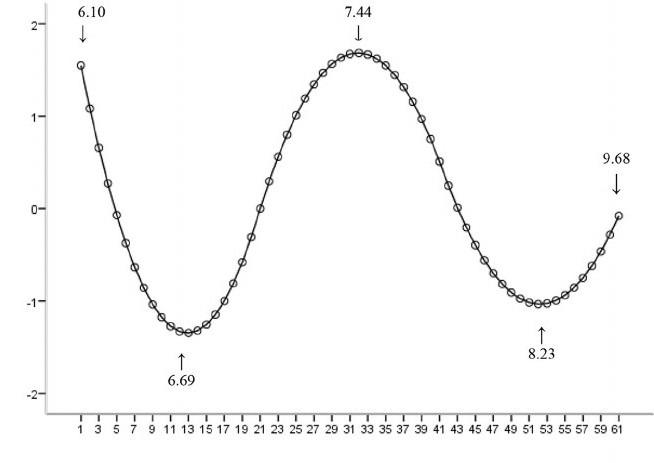
Υπολογισμός ισχύος και μεγέθους δείγματος

Εδώ, κατά κανόνα, δεν υπάρχουν συνεπείς μέθοδοι σχετικά με τον αριθμό των παρατηρήσεων σε σύγκριση με τον αριθμό των ανεξάρτητων μεταβλητών στο μοντέλο. Ο πρώτος κανόνας προτάθηκε από τους Good και Hardin και μοιάζει με N = t ^ n, όπου N είναι το μέγεθος δείγματος, n είναι ο αριθμός ανεξάρτητων μεταβλητών και t είναι ο αριθμός των παρατηρήσεων που απαιτούνται για την επίτευξη της επιθυμητής ακρίβειας, εάν το μοντέλο είχε μόνο μία ανεξάρτητη μεταβλητή. Για παράδειγμα, ένας ερευνητής δημιουργεί ένα μοντέλο γραμμικής παλινδρόμησης χρησιμοποιώντας ένα σύνολο δεδομένων που περιέχει 1000 ασθενείς (N). Εάν ο ερευνητής αποφασίσει ότι απαιτούνται πέντε παρατηρήσεις για τον ακριβή προσδιορισμό της γραμμής (m), τότε ο μέγιστος αριθμός ανεξάρτητων μεταβλητών που μπορεί να υποστηρίξει το μοντέλο είναι 4.

Άλλες μέθοδοι

Παρά το γεγονός ότι οι παράμετροι του μοντέλου παλινδρόμησης συνήθως υπολογίζονται χρησιμοποιώντας τη μέθοδο των ελάχιστων τετραγώνων, υπάρχουν και άλλες μέθοδοι που χρησιμοποιούνται πολύ λιγότερο συχνά. Για παράδειγμα, αυτές είναι οι ακόλουθες μέθοδοι:

• Bayesian μεθόδους (π.χ. μέθοδος Bayesian γραμμική παλινδρόμηση).
• Ποσοστό παλινδρόμησης, που χρησιμοποιείται σε καταστάσεις όπου η μείωση των ποσοστών σφαλμάτων θεωρείται πιο κατάλληλη.
• Οι μικρότερες απόλυτες αποκλίσεις, οι οποίες είναι πιο σταθερές παρουσία υπερβολικών τιμών που οδηγούν σε ποσοτική παλινδρόμηση.
• Μη παραμετρική παλινδρόμηση, απαιτώντας μεγάλο αριθμό παρατηρήσεων και υπολογισμών.
• Η απόσταση της μέτρησης μάθησης, η οποία μελετάται σε αναζήτηση μιας σημαντικής μετρικής απόστασης σε ένα δεδομένο χώρο εισόδου.

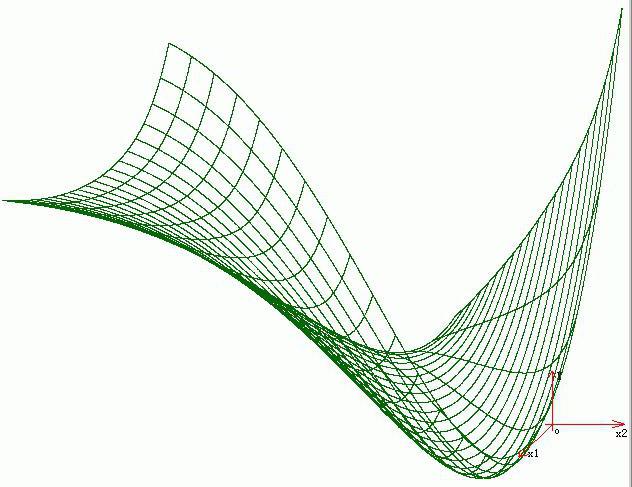
Λογισμικό

Όλα τα μεγάλα στατιστικά πακέτα λογισμικού εκτελούνται χρησιμοποιώντας ανάλυση παλινδρόμησης ελαχίστων τετραγώνων. Απλή ανάλυση γραμμικής παλινδρόμησης και πολλαπλής παλινδρόμησης μπορεί να χρησιμοποιηθεί σε ορισμένες εφαρμογές υπολογιστικού φύλλου, καθώς και σε ορισμένους υπολογιστές. Αν και πολλά στατιστικά πακέτα λογισμικού μπορούν να εκτελέσουν διάφορους τύπους μη παραμετρικής και αξιόπιστης παλινδρόμησης, αυτές οι μέθοδοι είναι λιγότερο τυποποιημένες. διαφορετικά πακέτα λογισμικού εφαρμόζουν διαφορετικές μεθόδους. Εξειδικευμένο λογισμικό παλινδρόμησης έχει αναπτυχθεί για χρήση σε τομείς όπως ανάλυση ανάλυσης και νευροαπεικόνιση.