Το "Στοχαστικό" είναι μια λέξη που χρησιμοποιούν οι φυσικοί, οι μαθηματικοί και άλλοι επιστήμονες για να περιγράψουν διαδικασίες που έχουν ένα στοιχείο τύχης. Η καταγωγή της είναι αρχαία ελληνική. Μεταφρασμένο σημαίνει "ικανό να μαντέψει".
Σημασία της λέξης "στοχαστική"

Το "Στοχαστικό" είναι μια έννοια που χρησιμοποιείται σε πολλά διαφορετικά πεδία της επιστήμης. Σημαίνει τυχαία, τυχαία, αβεβαιότητα κάτι. Στην ηθική του Αριστοτέλη (το γλυπτό πορτρέτο του παρουσιάζεται παραπάνω), η έννοια του "στοχαστικού" είναι ένας ορισμός που αναφέρεται στην ικανότητα να μαντέψει. Προφανώς, οι μαθηματικοί το χρησιμοποίησαν με βάση το ότι το στοιχείο τύχης εμφανίζεται μόνο όταν είναι απαραίτητο να μαντέψουμε. Η λέξη "στοχαστική" είναι μια έννοια που ορίζεται στο Νέο Διεθνές Λεξικό ως "εικαστική".
Έτσι, μπορεί να σημειωθεί ότι η τεχνική έννοια αυτής της έννοιας δεν αντιστοιχεί ακριβώς στο νόημά της (λεξικό). Ορισμένοι συγγραφείς χρησιμοποιούν την έκφραση "στοχαστική διαδικασία" ως συνώνυμο του όρου "τυχαία διαδικασία".
Στοχαστικότητα στα μαθηματικά

Η χρήση αυτού του όρου στα μαθηματικά είναι επί του παρόντος ευρέως διαδεδομένη. Για παράδειγμα, υπάρχει μια τέτοια έννοια στην θεωρία πιθανοτήτων ως στοχαστική διαδικασία. Το αποτέλεσμά του δεν μπορεί να προσδιοριστεί από την αρχική κατάσταση αυτού του συστήματος.
Η χρήση στα μαθηματικά της έννοιας της «στοχαστικότητας» αποδίδεται στα έργα του Vladislav Bortskevich. Ήταν αυτός που χρησιμοποίησε τον όρο κατά την έννοια των "υποβληθεισών υποθέσεων". Στα μαθηματικά, ειδικά σε ένα τέτοιο τμήμα αυτής της επιστήμης ως θεωρία πιθανοτήτων, το πεδίο της τυχαίας έρευνας παίζει σημαντικό ρόλο. Υπάρχει, για παράδειγμα, μια τέτοια στοχαστική μήτρα. Οι στήλες ή οι σειρές αυτού του πίνακα αντιστοιχούν σε ένα.
Στοχαστικά Μαθηματικά (Οικονομικά)
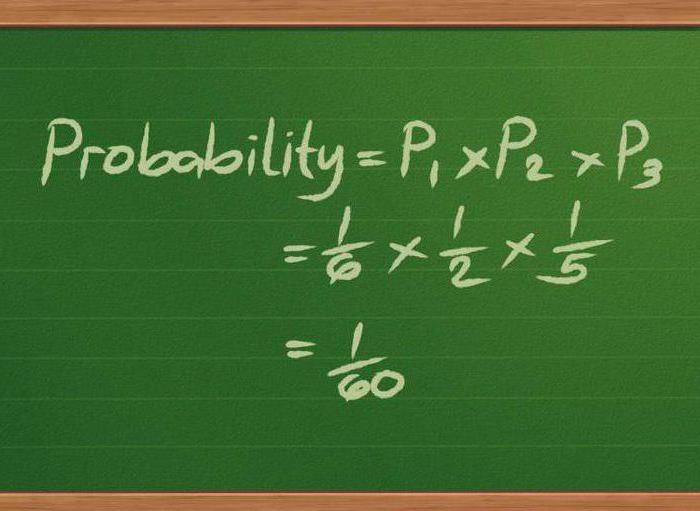
Αυτό το τμήμα των μαθηματικών αναλύει τις οικονομικές δομές που λειτουργούν υπό συνθήκες αβεβαιότητας. Έχει σχεδιαστεί για να βρει τις πιο ορθολογικές μεθόδους διαχείρισης των χρηματοοικονομικών περιουσιακών στοιχείων και δομών, λαμβάνοντας υπόψη παράγοντες όπως η στοχαστική εξέλιξη, ο κίνδυνος, ο χρόνος κλπ.
Στην επιστήμη, είναι συνηθισμένο να διακρίνουμε τις ακόλουθες δομές και αντικείμενα που χρησιμοποιούνται στα οικονομικά μαθηματικά ως σύνολο:
- επιχειρήσεις (για παράδειγμα, εταιρείες) ·
- άτομα ·
- ενδιάμεσες δομές (συνταξιοδοτικά ταμεία, τράπεζες) ·
- χρηματοπιστωτικές αγορές.
Το κύριο αντικείμενο μελέτης των στοχαστικών οικονομικών μαθηματικών είναι ακριβώς το τελευταίο από αυτά. Αυτή η ενότητα βασίζεται σε τέτοιου είδους κλάδους όπως στατιστικές τυχαίων διεργασιών, θεωρία τυχαίων διεργασιών κλπ.
Επί του παρόντος, ακόμη και άνθρωποι μακριά από την επιστήμη, είναι γνωστό από πολυάριθμες ειδήσεις και δημοσιεύματα στα μέσα ενημέρωσης ότι οι αξίες των λεγόμενων παγκόσμιων χρηματοοικονομικών δεικτών (για παράδειγμα, ο δείκτης Dow Jones), οι τιμές των μετοχών αλλάζουν τυχαία. Ο L. Bachelier έκανε την πρώτη προσπάθεια να περιγράψει χρησιμοποιώντας τα μαθηματικά την εξέλιξη των τιμών των μετοχών. Η στοχαστική μέθοδος βασίζεται στη θεωρία πιθανοτήτων. Η διατριβή του L. Bachelier, που παρουσιάζει αυτή την απόπειρα, δημοσιεύθηκε το 1900. Ο επιστήμονας έχει αποδείξει τον τύπο που σήμερα είναι γνωστός ως ο τύπος της εύλογης αξίας για τις επιλογές κλήσεων. Αντικατοπτρίζει την στοχαστική πιθανότητα.
Σημαντικές ιδέες που στη συνέχεια οδήγησαν στην εμφάνιση μιας πραγματικής θεωρίας της αγοράς παρουσιάστηκαν στο έργο του Μ. Kendall, που δημοσιεύθηκε το 1953. Το παρόν έγγραφο ασχολείται με το ζήτημα της δυναμικής των τιμών των μετοχών. Ο ερευνητής το περιγράφει χρησιμοποιώντας στοχαστικές διαδικασίες.
Στοχαστικότητα στη Φυσική
Χάρη στους φυσικούς E. Fermi, S. Ulam, N. Metropolis και D.Ο Neumann χρησιμοποιείται ευρέως στη μέθοδο Monte Carlo. Το όνομά του προέρχεται από ένα καζίνο που βρίσκεται στην ίδια πόλη σε μια χώρα όπως το Μονακό. Ήταν εδώ ότι ο θείος Ulam δανείστηκε χρήματα για το παιχνίδι. Χρησιμοποιώντας τη φύση της επανάληψης και της πιθανότητας να μελετήσετε τις διαδικασίες είναι παρόμοια με αυτό που συμβαίνει σε ένα καζίνο.

Κατά την εφαρμογή αυτής της μεθόδου μοντελοποίησης, πρώτα διερευνάται ένα πιθανοτικό ανάλογο. Πριν από αυτό, η μοντελοποίηση πραγματοποιήθηκε στην αντίθετη κατεύθυνση: χρησιμοποιήθηκε για να επαληθεύσει το αποτέλεσμα του προκαθορισμένου ντετερμινιστικού προβλήματος. Παρόλο που παρόμοιες προσεγγίσεις υπήρχαν πριν από την ανακάλυψη της μεθόδου Monte Carlo, δεν ήταν δημοφιλείς και γενικές.
Ο Enrico Fermi το 1930 εφάρμοσε στοχαστικές τεχνικές για τον υπολογισμό των ιδιοτήτων του νετρονίου, το οποίο είχε μόλις ανακαλυφθεί εκείνη την εποχή. Οι μέθοδοι Monte Carlo χρησιμοποιήθηκαν αργότερα κατά την εργασία στο έργο του Μανχάταν, αν και εκείνη τη στιγμή οι δυνατότητες των υπολογιστών ήταν σημαντικά περιορισμένες. Για το λόγο αυτό, έγιναν ευρέως διαδεδομένα μόνο μετά την εμφάνιση υπολογιστών.
Στοχαστικά σήματα
Τα κανονικά και στοχαστικά σήματα έχουν διαφορετικές κυματομορφές. Εάν επαναμετρήσουμε το τελευταίο, έχουμε ταλαντώσεις που έχουν ένα νέο σχήμα, το οποίο είναι διαφορετικό από το προηγούμενο, αλλά παρουσιάζει μια ορισμένη ομοιότητα στα βασικά χαρακτηριστικά. Ένα παράδειγμα στοχαστικού σήματος είναι η καταγραφή των ταλαντώσεων των θαλάσσιων κυμάτων.
Γιατί είναι απαραίτητο να μιλήσουμε για αυτά τα μάλλον ασυνήθιστα σήματα; Το γεγονός είναι ότι στη μελέτη των αυτόματων συστημάτων, είναι ακόμη πιο κοινά από ό, τι προβλεπόταν.
Στοχαστικότητα και Τεχνητή Νοημοσύνη
Τα στοχαστικά προγράμματα τεχνητής νοημοσύνης λειτουργούν με πιθανοτικές μεθόδους. Αλγόριθμοι όπως η στοχαστική βελτιστοποίηση ή τα νευρωνικά δίκτυα μπορούν να αναφερθούν ως παράδειγμα. Το ίδιο ισχύει και για τους προσομοιωμένους ανασυνδυασμούς και τους γενετικούς αλγόριθμους. Σε όλες αυτές τις περιπτώσεις, η στοχαστικότητα μπορεί να περιέχεται στο πρόβλημα ως τέτοιο ή στο σχεδιασμό κάτι υπό την προϋπόθεση της αβεβαιότητας. Το ντετερμινιστικό περιβάλλον για έναν παράγοντα μοντελοποίησης είναι απλούστερο από το στοχαστικό.

Έτσι, όπως βλέπουμε, η έννοια του ενδιαφέροντος μας χρησιμοποιείται σε πολλά πεδία της επιστήμης. Έχουμε καταγράψει και χαρακτηρίσει μόνο τους κύριους τομείς της εφαρμογής του. Η μελέτη όλων αυτών των διαδικασιών, όπως βλέπετε, είναι πολύ σημαντική και συναφής. Αυτός είναι ο λόγος για τον οποίο η έννοια του ενδιαφέροντος για εμάς είναι πιθανό να χρησιμοποιηθεί για μεγάλο χρονικό διάστημα στην επιστήμη.








