Análisis de correlación y regresión: ejemplo, tareas, aplicación. Método de análisis de correlación y regresión.

Análisis de regresión de correlación - Este es uno de los métodos más comunes para estudiar la relación entre valores numéricos. Su objetivo principal es encontrar la relación entre los dos parámetros y su grado con la derivación posterior de la ecuación. Por ejemplo, tenemos estudiantes que aprobaron el examen de matemáticas e inglés. Podemos usar la correlación para determinar si el éxito de una prueba afecta los resultados en otra materia. Con respecto al análisis de regresión, ayuda a predecir las calificaciones de matemáticas en función de los puntos obtenidos en un examen de inglés, y viceversa.

¿Qué es un cuadro de correlación?

Cualquier análisis comienza con la recopilación de información. Cuanto más es, más exactamente el resultado obtenido al final. En el ejemplo anterior, tenemos dos disciplinas en las cuales los estudiantes necesitan aprobar un examen. Su tasa de éxito es una estimación. El análisis de correlación-regresión muestra si el resultado de una asignatura afecta los puntos obtenidos en el segundo examen. Para responder a esta pregunta, es necesario analizar las calificaciones de todos los estudiantes en paralelo. Pero primero debe decidir sobre la variable dependiente. En este caso, no es tan importante. Supongamos que un examen de matemáticas se realizó antes. Los puntos en él son una variable independiente (se posponen a lo largo de la abscisa). El inglés está en el horario más tarde. Por lo tanto, las estimaciones basadas en ella son una variable dependiente (se trazan a lo largo de la ordenada). Cuanto más se parezca la gráfica así obtenida como una línea recta, mayor será la correlación lineal entre los dos valores seleccionados. Esto significa que los estudiantes de matemáticas tienen más probabilidades de obtener cinco en el examen de inglés.

Suposiciones y simplificaciones

El método de análisis de correlación y regresión implica encontrar una relación causal. Sin embargo, en la primera etapa, debe comprender que los cambios en ambas cantidades pueden deberse a un tercio que aún no ha sido considerado por el investigador. También puede haber relaciones no lineales entre las variables, por lo tanto, obtener un coeficiente igual a cero no es el final del experimento.

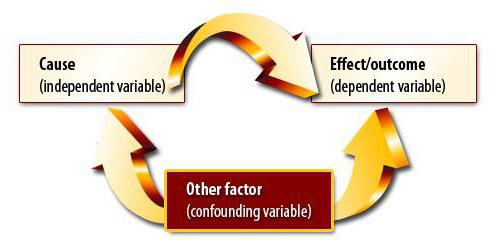
Correlación lineal de Pearson

Este coeficiente se puede usar sujeto a dos condiciones. El primero, todos los valores de las variables son números racionales, el segundo, se espera que los valores cambien proporcionalmente. Este coeficiente siempre está entre -1 y 1. Si es mayor que cero, entonces hay una dependencia directamente proporcional, menor, inversamente, igual, estos valores no se afectan entre sí de ninguna manera. La capacidad de calcular este indicador es la base del análisis de correlación y regresión. Por primera vez, este coeficiente fue desarrollado por Karl Pearson basado en la idea de Francis Galton.

Propiedades y precauciones

El coeficiente de correlación de Pearson es una herramienta poderosa, pero también debe usarse con precaución. Se utilizan las siguientes advertencias:

1. El coeficiente de Pearson indica la presencia o ausencia de una relación lineal. El análisis de correlación-regresión no termina allí, puede resultar que las variables estén interconectadas.
2. Hay que tener cuidado al interpretar el valor del coeficiente. Se puede encontrar una correlación entre el tamaño de la pierna y el nivel de coeficiente intelectual.Pero esto no significa que un indicador determine a otro.
3. El coeficiente de Pearson no dice nada sobre la relación causal entre los indicadores.

Coeficiente de correlación de rango de Spearman

Si un cambio en el valor de un indicador conduce a un aumento o disminución en el valor de otro, entonces esto significa que están relacionados. El análisis de correlación-regresión, cuyo ejemplo se proporcionará a continuación, está conectado con precisión con dichos parámetros. El coeficiente de clasificación le permite simplificar los cálculos.

Análisis de correlación y regresión: un ejemplo

Supongamos que hay una evaluación de la efectividad de diez empresas. Tenemos dos jueces que les dan puntos. El análisis de correlación y regresión de la empresa en este caso no puede llevarse a cabo sobre la base del coeficiente lineal de Pearson. No nos interesa la relación entre las calificaciones de los jueces. Las filas de las empresas según los jueces son importantes.

Este tipo de análisis tiene las siguientes ventajas:

• Forma no paramétrica de las relaciones entre las cantidades estudiadas.
• Facilidad de uso, porque los rangos se pueden atribuir tanto en orden ascendente de valor como en orden descendente.

El único requisito de este tipo de análisis es la necesidad de convertir los datos de origen.

Problemas de aplicación

El análisis de correlación y regresión se basa en los siguientes supuestos:

• Las observaciones se consideran independientes (una pérdida de cinco veces del "águila" no afecta el resultado del próximo lanzamiento de la moneda).
• En el análisis de correlación, ambas variables se consideran aleatorias. En regresión, solo uno (dependiente).
• Al probar una hipótesis, se debe observar una distribución normal. El cambio en la variable dependiente debe ser el mismo para cada valor en la abscisa.
• El diagrama de correlación es solo la primera prueba de la hipótesis sobre la relación entre las dos series de parámetros, y no el resultado final del análisis.

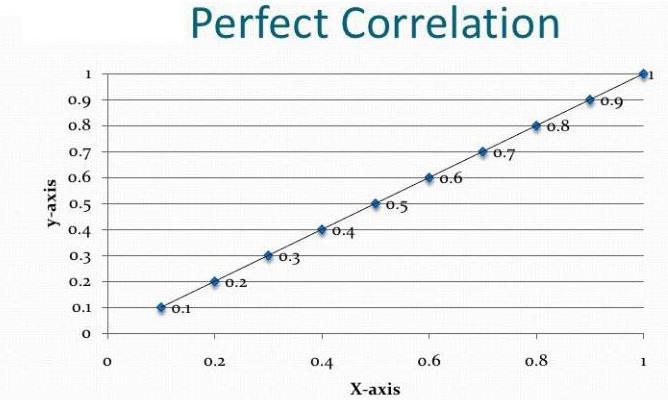
Dependencia y causalidad

Supongamos que hemos calculado el coeficiente de correlación del volumen de exportación y el PIB. Resultó ser igual al módulo de unidad. ¿Hemos hecho análisis de correlación y regresión hasta el final? Por supuesto que no. El resultado obtenido no significa en absoluto que el PIB pueda expresarse a través de la exportación. Todavía no hemos demostrado una relación causal entre los indicadores. Análisis de correlación-regresión: pronostica los valores de una variable en función de otra. Sin embargo, debe comprender que a menudo muchos factores afectan el parámetro. La exportación determina el PIB, pero no solo eso. Hay otros factores Aquí hay una correlación y una relación causal, aunque ajustada para otros componentes del producto interno bruto.

Otra situación es mucho más peligrosa. En el Reino Unido, se realizó una encuesta que mostró que los niños cuyos padres fumaban eran con mayor frecuencia delincuentes. Esta conclusión se basa en una fuerte correlación entre el indicador. ¿Pero es correcto? En primer lugar, la dependencia podría ser inversa. Los padres podrían comenzar a fumar debido al estrés por el hecho de que sus hijos constantemente sufren alteraciones y violan la ley. En segundo lugar, ambos parámetros pueden deberse al tercero. Estas familias pertenecen a clases sociales bajas, que se caracterizan por ambos problemas. Por lo tanto, con base en la correlación, no se puede concluir que existe una relación causal.

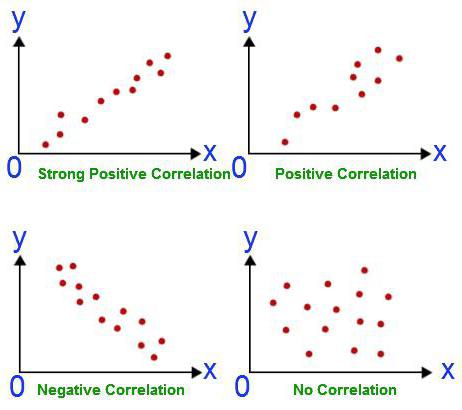
¿Por qué usar análisis de regresión?

La dependencia de correlación implica encontrar relaciones entre cantidades. La relación causal en este caso permanece detrás de escena. Las tareas de análisis de correlación y regresión coinciden solo en términos de confirmar la existencia de una relación entre los valores de dos cantidades. Sin embargo, inicialmente el investigador no presta atención a la posibilidad de una relación causal. El análisis de regresión siempre tiene dos variables, una de las cuales es dependiente. Se lleva a cabo en varias etapas:

1. Elegir el modelo correcto utilizando el método de mínimos cuadrados.
2. Derivación de una ecuación que describe el efecto de un cambio en una variable independiente en otra.

Por ejemplo, si estudiamos el efecto de la edad en el crecimiento humano, un análisis de regresión puede ayudar a predecir cambios a lo largo de los años.

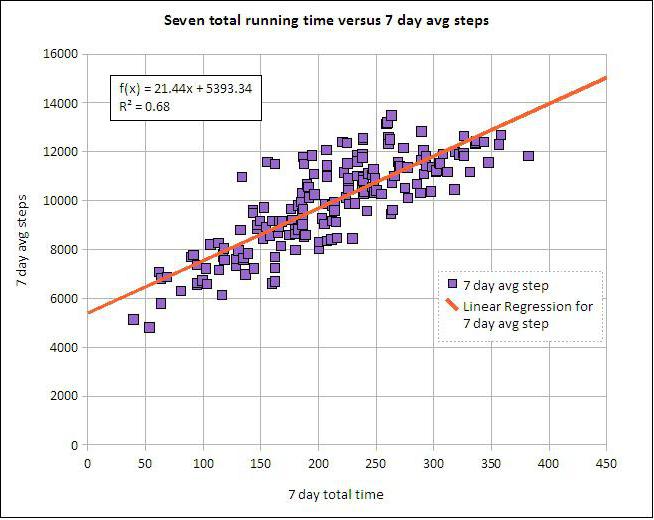
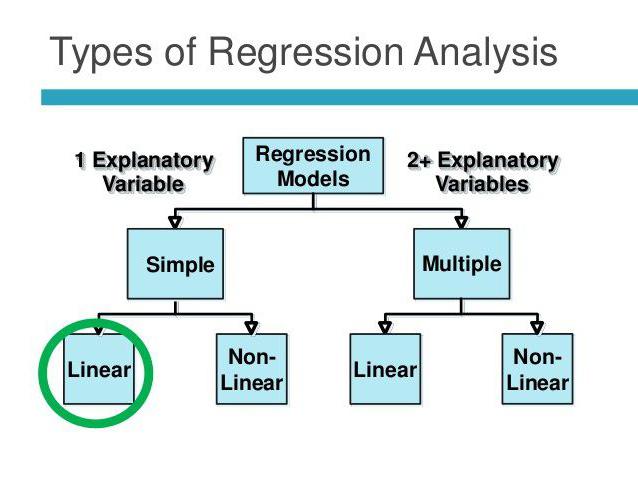
Regresión lineal y múltiple

Supongamos que X e Y son dos variables relacionadas. El análisis de regresión nos permite predecir la magnitud de uno de ellos en función de los valores del otro. Por ejemplo, la madurez y la edad son síntomas dependientes. La relación entre ellos se refleja mediante regresión lineal. De hecho, puede expresar X a través de Y o viceversa. Pero a menudo solo una de las líneas de regresión es correcta. El éxito del análisis depende en gran medida de la determinación correcta de la variable independiente. Por ejemplo, tenemos dos indicadores: rendimiento y precipitación. De la experiencia cotidiana, queda claro que lo primero depende de lo segundo, y no al revés.

La regresión múltiple le permite calcular un valor desconocido basado en los valores de tres o más variables. Por ejemplo, el rendimiento de arroz por acre de tierra depende de la calidad del grano, la fertilidad del suelo, los fertilizantes, la temperatura y las precipitaciones. Todos estos parámetros afectan el resultado general. Para simplificar el modelo, se utilizan los siguientes supuestos:

• La relación entre características independientes e influyentes es lineal.
• Se excluye la multicolinealidad. Esto significa que las variables dependientes no están interconectadas.
• Homocedasticidad y normalidad de series de números.

El uso de análisis de correlación y regresión.

Hay tres casos principales de usar este método:

1. Prueba de relaciones casuales entre cantidades. En este caso, el investigador determina los valores de la variable y descubre si afectan el cambio en la variable dependiente. Por ejemplo, puede dar a las personas diferentes dosis de alcohol y medir su presión arterial. En este caso, el investigador sabe con certeza que el primero es la causa del segundo, y no al revés. El análisis de correlación-regresión le permite detectar una relación lineal directamente proporcional entre estas dos variables y derivar una fórmula que la describa. En este caso, se pueden comparar valores expresados ​​en unidades de medida completamente diferentes.
2. Encontrar una relación entre dos variables sin extender una relación causal a ellas. En este caso, no hay diferencia de qué tamaño el investigador llama dependiente. Además, en realidad, puede resultar que ambos se vean afectados por la tercera variable, por lo tanto, cambian proporcionalmente.
3. Cálculo de los valores de una cantidad en base a otra. Se basa en una ecuación en la que se sustituyen números conocidos.

Por lo tanto, el análisis de correlación implica encontrar una conexión (no causal) entre variables, y el análisis de regresión lo explica, a menudo utilizando una función matemática.