El análisis de regresión es un método estadístico para estudiar la dependencia de una variable aleatoria de las variables.

En el modelado estadístico, el análisis de regresión es un estudio utilizado para evaluar la relación entre variables. Este método matemático incluye muchos otros métodos para modelar y analizar varias variables, cuando el foco está en la relación entre la variable dependiente y una o más independientes. Más específicamente, el análisis de regresión ayuda a comprender cómo cambia un valor típico de una variable dependiente si una de las variables independientes cambia, mientras que las otras variables independientes permanecen fijas.

En todos los casos, la estimación objetivo es una función de variables independientes y se llama función de regresión. En el análisis de regresión, también es interesante caracterizar el cambio en la variable dependiente como una función de regresión, que puede describirse utilizando una distribución de probabilidad.

Tareas de análisis de regresión

Este método de investigación estadística se usa ampliamente para pronosticar, donde su uso tiene una ventaja significativa, pero a veces puede conducir a ilusiones o relaciones falsas, por lo tanto, se recomienda usarlo cuidadosamente en este tema, porque, por ejemplo, la correlación no significa una relación causal.

Se ha desarrollado una gran cantidad de métodos para realizar análisis de regresión, como la regresión lineal y ordinaria de mínimos cuadrados, que son paramétricos. Su esencia es que la función de regresión se define en términos de un número finito de parámetros desconocidos que se estiman a partir de los datos. La regresión no paramétrica permite que sus funciones se encuentren en un determinado conjunto de funciones, que pueden ser de dimensión infinita.

Como método de investigación estadística, el análisis de regresión en la práctica depende de la forma del proceso de generación de datos y de cómo se relaciona con el enfoque de regresión. Dado que la forma verdadera del proceso de datos está generando, por regla general, un número desconocido, el análisis de regresión de los datos a menudo depende en cierta medida de los supuestos sobre este proceso. Estas suposiciones a veces se verifican si hay suficientes datos disponibles. Los modelos de regresión a menudo son útiles incluso cuando los supuestos se violan moderadamente, aunque no pueden funcionar con la máxima eficiencia.

En un sentido más restringido, la regresión puede relacionarse específicamente con la evaluación de las variables de respuesta continua, en contraste con las variables de respuesta discreta utilizadas en la clasificación. El caso de una variable de salida continua también se denomina regresión métrica para distinguirla de los problemas relacionados.

La historia

La primera forma de regresión es el conocido método de mínimos cuadrados. Fue publicado por Legendre en 1805 y Gauss en 1809. Legendre y Gauss aplicaron el método a la tarea de determinar a partir de observaciones astronómicas las órbitas de los cuerpos alrededor del Sol (principalmente cometas, pero más tarde descubrieron planetas menores). Gauss publicó un desarrollo adicional de la teoría de los mínimos cuadrados en 1821, incluida una versión del teorema de Gauss-Markov.

El término "regresión" fue acuñado por Francis Galton en el siglo XIX para describir un fenómeno biológico. La conclusión fue que el crecimiento de los descendientes a partir del crecimiento de los antepasados, por regla general, regresa al promedio normal.Para Galton, la regresión solo tenía este significado biológico, pero luego su trabajo fue continuado por Udney Yule y Karl Pearson y llevado a un contexto estadístico más general. En el trabajo de Yule y Pearson, la distribución conjunta de las variables de respuesta y las variables explicativas se considera gaussiana. Esta suposición fue rechazada por Fisher en los trabajos de 1922 y 1925. Fisher sugirió que la distribución condicional de la variable de respuesta es gaussiana, pero la distribución conjunta no debería serlo. En este sentido, la suposición de Fischer está más cerca de la formulación de Gauss de 1821. Hasta 1970, a veces tomaba hasta 24 horas obtener el resultado de un análisis de regresión.

Los métodos de análisis de regresión continúan siendo un área de investigación activa. En las últimas décadas, se han desarrollado nuevos métodos para una regresión confiable; regresión que implica respuestas correlacionadas; métodos de regresión que acomodan varios tipos de datos faltantes; regresión no paramétrica; Métodos de regresión bayesiana; regresiones en las cuales las variables predictoras se miden con un error; regresiones con más predictores que observaciones, así como inferencias causales con regresión.

Modelos de regresión

Los modelos de análisis de regresión incluyen las siguientes variables:

• Parámetros desconocidos, designados como beta, que pueden ser escalares o vectoriales.
• Variables independientes, X.
• Variables dependientes, Y.

En varios campos de la ciencia donde se aplica el análisis de regresión, se usan varios términos en lugar de variables dependientes e independientes, pero en todos los casos el modelo de regresión relaciona Y con las funciones X y β.

La aproximación generalmente toma la forma E (Y | X) = F (X, β). Para realizar un análisis de regresión, se debe determinar el tipo de función f. Con menos frecuencia, se basa en el conocimiento de la relación entre Y y X que no dependen de los datos. Si dicho conocimiento no está disponible, entonces se elige una forma F flexible o conveniente.

Variable dependiente Y

Ahora suponga que el vector de parámetros desconocidos β tiene una longitud k. Para realizar un análisis de regresión, el usuario debe proporcionar información sobre la variable dependiente Y:

• Si hay N puntos de datos de la forma (Y, X), donde N

• Si se observa exactamente N = K, y la función F es lineal, entonces la ecuación Y = F (X, β) puede resolverse exactamente, y no aproximadamente. Esto se reduce a resolver un conjunto de N ecuaciones con N incógnitas (elementos de β), que tiene una solución única siempre que X sea linealmente independiente. Si F no es lineal, la solución puede no existir o pueden existir muchas soluciones.
• La más común es la situación en la que se observan N> puntos a los datos. En este caso, hay suficiente información en los datos para evaluar el valor único para β que mejor coincide con los datos, y el modelo de regresión, cuando se aplica a los datos, puede considerarse como un sistema sobredeterminado en β.

En el último caso, el análisis de regresión proporciona herramientas para:

• Encontrar soluciones para parámetros desconocidos β, que, por ejemplo, minimizarán la distancia entre los valores medidos y predichos de Y.
• Bajo ciertos supuestos estadísticos, el análisis de regresión usa información en exceso para proporcionar información estadística sobre parámetros desconocidos β y los valores predichos de la variable dependiente Y.

Número necesario de mediciones independientes.

Considere un modelo de regresión que tiene tres parámetros desconocidos: β₀, β₁ y β₂. Suponga que el experimentador realiza 10 mediciones en el mismo valor de la variable independiente del vector X.En este caso, el análisis de regresión no proporciona un conjunto único de valores. Lo mejor que puede hacer es evaluar la media y la desviación estándar de la variable dependiente Y. Al medir dos valores X diferentes de la misma manera, puede obtener suficientes datos para una regresión con dos incógnitas, pero no para tres o más incógnitas.

Si las mediciones del experimentador se llevaron a cabo en tres valores diferentes de la variable independiente del vector X, entonces el análisis de regresión proporcionará un conjunto único de estimaciones para tres parámetros desconocidos en β.

En el caso de regresión lineal general, la declaración anterior es equivalente al requisito de que la matriz X^TX es reversible.

Suposiciones estadísticas

Cuando el número de mediciones N es mayor que el número de parámetros desconocidos k y el error de medición ε_yo, luego, como regla, el exceso de información contenida en las mediciones se distribuye y se usa para pronósticos estadísticos con respecto a parámetros desconocidos. Este exceso de información se denomina grado de libertad de regresión.

Suposiciones fundamentales

Los supuestos clásicos para el análisis de regresión incluyen:

• La muestra es representativa de la predicción de inferencia.
• El error es una variable aleatoria con un valor promedio de cero, que está condicionada a las variables explicativas.
• Las variables independientes se miden sin error.
• Como variables independientes (predictores), son linealmente independientes, es decir, no es posible expresar ningún predictor en forma de una combinación lineal de los demás.
• Los errores no están correlacionados, es decir, la matriz de covarianza de los errores diagonales y cada elemento distinto de cero son la varianza del error.
• La varianza del error es constante según las observaciones (homoscedasticidad). Si no, puede usar el método de mínimos cuadrados ponderados u otros métodos.

Estas condiciones suficientes para la estimación de mínimos cuadrados poseen las propiedades requeridas, en particular, estos supuestos significan que las estimaciones de parámetros serán objetivas, consistentes y efectivas, especialmente cuando se tienen en cuenta en la clase de estimaciones lineales. Es importante tener en cuenta que la evidencia rara vez cumple con las condiciones. Es decir, el método se usa incluso si los supuestos no son ciertos. En ocasiones, se puede usar una variación de supuestos como una medida de la utilidad de este modelo. Muchos de estos supuestos pueden mitigarse mediante métodos más avanzados. Los informes de análisis estadístico generalmente incluyen análisis de pruebas basadas en datos de muestra y metodología para la utilidad del modelo.

Además, las variables en algunos casos se refieren a valores medidos en ubicaciones de puntos. Puede haber tendencias espaciales y autocorrelación espacial en variables que violan los supuestos estadísticos. La regresión geográfica ponderada es el único método que se ocupa de dichos datos.

Análisis de regresión lineal

En la regresión lineal, una característica es que la variable dependiente, que es Y_yoEs una combinación lineal de parámetros. Por ejemplo, en una regresión lineal simple, una variable independiente, x, se usa para modelar n-puntos_yoy dos parámetros, β₀ y β₁.

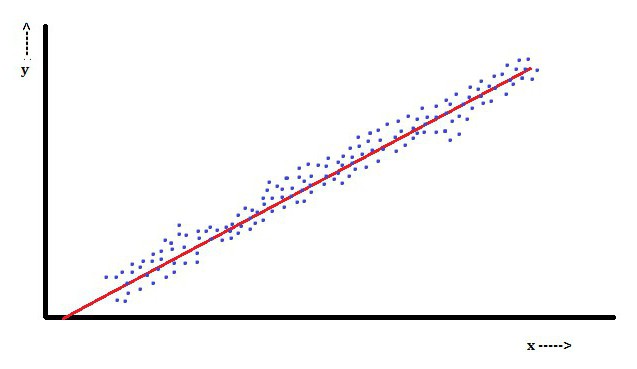
Con la regresión lineal múltiple, hay varias variables independientes o sus funciones.

Con un muestreo aleatorio de una población, sus parámetros permiten obtener un ejemplo de un modelo de regresión lineal.

En este aspecto, el método de mínimos cuadrados es el más popular. Utilizándolo, se obtienen estimaciones de parámetros que minimizan la suma de los residuos al cuadrado. Este tipo de minimización (que es característica de una regresión lineal) de esta función conduce a un conjunto de ecuaciones normales y un conjunto de ecuaciones lineales con parámetros que se resuelven para obtener estimaciones de parámetros.

Bajo el supuesto adicional de que el error de la población generalmente se extiende, el investigador puede usar estas estimaciones de errores estándar para crear intervalos de confianza y probar hipótesis sobre sus parámetros.

Análisis de regresión no lineal

Un ejemplo en el que la función no es lineal con respecto a los parámetros indica que la suma de los cuadrados debe minimizarse utilizando un procedimiento iterativo. Esto introduce muchas complicaciones que determinan las diferencias entre los métodos de mínimos cuadrados lineales y no lineales. En consecuencia, los resultados del análisis de regresión utilizando el método no lineal a veces son impredecibles.

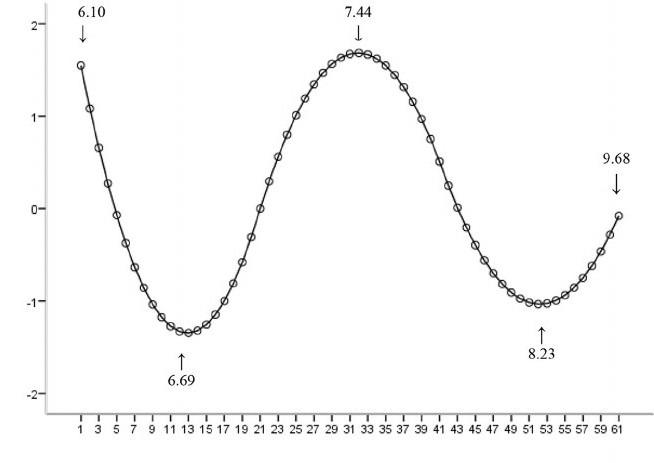
Cálculo de potencia y tamaño de muestra.

Aquí, como regla, no hay métodos consistentes con respecto al número de observaciones en comparación con el número de variables independientes en el modelo. Good y Hardin propusieron la primera regla y se parece a N = t ^ n, donde N es el tamaño de la muestra, n es el número de variables independientes yt es el número de observaciones necesarias para lograr la precisión deseada si el modelo tuviera solo una variable independiente. Por ejemplo, un investigador crea un modelo de regresión lineal utilizando un conjunto de datos que contiene 1000 pacientes (N). Si el investigador decide que se necesitan cinco observaciones para determinar con precisión la línea (m), entonces el número máximo de variables independientes que el modelo puede admitir es 4.

Otros métodos

A pesar de que los parámetros del modelo de regresión generalmente se estiman utilizando el método de mínimos cuadrados, existen otros métodos que se utilizan con mucha menos frecuencia. Por ejemplo, estos son los siguientes métodos:

• Métodos bayesianos (por ejemplo, método de regresión lineal bayesiano).
• Regresión porcentual, utilizada para situaciones en las que una reducción en los errores porcentuales se considera más apropiada.
• Las desviaciones absolutas más pequeñas, que son más estables en presencia de valores atípicos que conducen a la regresión cuantil.
• Regresión no paramétrica, que requiere una gran cantidad de observaciones y cálculos.
• La distancia de la métrica de aprendizaje, que se estudia en busca de una distancia métrica significativa en un espacio de entrada dado.

Software

Todos los paquetes de software estadísticos principales se realizan utilizando análisis de regresión de mínimos cuadrados. La regresión lineal simple y el análisis de regresión múltiple se pueden usar en algunas aplicaciones de hoja de cálculo, así como en algunas calculadoras. Aunque muchos paquetes de software estadístico pueden realizar varios tipos de regresión no paramétrica y confiable, estos métodos están menos estandarizados; diferentes paquetes de software implementan diferentes métodos. Se ha desarrollado un software de regresión especializado para su uso en áreas como análisis de examen y neuroimagen.