Korrelaatio regressioanalyysi - Tämä on yksi yleisimmistä menetelmistä numeeristen arvojen välisen suhteen tutkimiseksi. Sen päätavoite on löytää suhde kahden parametrin ja sen asteen välillä seuraavan yhtälön johdannaisen kanssa. Esimerkiksi meillä on opiskelijoita, jotka ovat läpäisseet matematiikan ja englannin tutkinnon. Voimme käyttää korrelaatiota selvittääkseen, vaikuttaako yhden testin onnistuminen toisen tutkimuksen tuloksiin. Regressioanalyysin suhteen se auttaa ennustamaan matematiikan arvosanoja englanninkielisessä tentissä saatujen pisteiden perusteella ja päinvastoin.

Mikä on korrelaatiokaavio?
Mahdolliset analyysit alkavat tiedonkeruulla. Mitä enemmän se on, sitä tarkemmin lopputulos saadaan. Yllä olevassa esimerkissä meillä on kaksi tieteenalaa, joissa opiskelijoiden on suoritettava koe. Heidän onnistumisaste on arvio. Korrelaatio-regressioanalyysi osoittaa, vaikuttaako yhden tutkimuksen tulos toisen tutkinnon pisteisiin. Kysymykseen vastaamiseksi on tarpeen analysoida kaikkien opiskelijoiden arvioinnit samanaikaisesti. Mutta ensin sinun on päätettävä riippuvasta muuttujasta. Tässä tapauksessa se ei ole niin tärkeä. Oletetaan, että matemaattiset kokeet pidettiin aikaisemmin. Sen pisteet ovat itsenäinen muuttuja (niitä lykätään abskissan suuntaan). Englanti on aikataulussa myöhemmin. Siksi siihen perustuvat arviot ovat riippuvainen muuttuja (on piirretty ordinaattia pitkin). Mitä enemmän näin saatu graafi näyttää suoralta, sitä vahvempi on lineaarinen korrelaatio kahden valitun arvon välillä. Tämä tarkoittaa, että matematiikan opiskelijat saavat todennäköisemmin viiden englannin kielen tentissä.
Oletukset ja yksinkertaistamiset
Korrelaatio- ja regressioanalyysimenetelmä sisältää syy-yhteyden löytämisen. Ensimmäisessä vaiheessa sinun on kuitenkin ymmärrettävä, että muutokset molemmissa määrissä voivat johtua jostain kolmannesta, jota tutkija ei vielä ole ottanut huomioon. Muuttujien välillä voi olla myös epälineaarisia suhteita, joten nolla-kertoimen saaminen ei ole kokeen loppu.
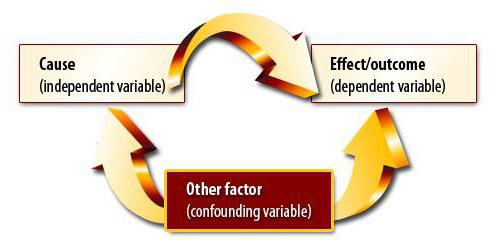
Pearsonin lineaarinen korrelaatio
Tätä kerrointa voidaan käyttää kahdessa tapauksessa. Ensimmäisen - kaikkien muuttujien arvot ovat rationaalisia lukuja, toisen - odotetaan arvojen muuttuvan suhteessa. Tämä kerroin on aina välillä -1 ja 1. Jos se on suurempi kuin nolla, syntyy suoraan verrannollinen riippuvuus, vähemmän - päinvastoin, yhtä suuri - nämä arvot eivät vaikuta toisiinsa millään tavalla. Kyky laskea tämä indikaattori on korrelaatio- ja regressioanalyysin perusta. Karl Pearson kehitti tämän kertoimen ensimmäistä kertaa Francis Galtonin ajatuksen perusteella.
Ominaisuudet ja varoitukset
Pearsonin korrelaatiokerroin on tehokas työkalu, mutta sitä tulisi myös käyttää varoen. Seuraavat varoitukset ovat käytössä:
- Pearson-kerroin osoittaa lineaarisen suhteen olemassaolon tai puuttumisen. Korrelaatio-regressioanalyysi ei lopu tähän, voi osoittautua, että muuttujat ovat silti kytketty toisiinsa.
- Kertoimen arvon tulkinnassa on oltava varovainen. Korrelaatio löytyy jalan koon ja IQ-tason välillä.Mutta tämä ei tarkoita, että yksi indikaattori määrittää toisen.
- Pearson-kerroin ei sano mitään indikaattorien välisestä syy-suhteesta.

Spearmanin sijoituskorrelaatiokerroin
Jos yhden indikaattorin arvon muutos johtaa toisen indikaattorin arvon nousuun tai laskuun, tämä tarkoittaa, että indikaattorit liittyvät toisiinsa. Korrelaatio-regressioanalyysi, josta esimerkki annetaan jäljempänä, liittyy tarkasti tällaisiin parametreihin. Sijoituskerroin antaa sinun yksinkertaistaa laskelmia.
Korrelaatio- ja regressioanalyysi: esimerkki
Oletetaan, että arvioidaan kymmenen yrityksen tehokkuutta. Meillä on kaksi tuomaria, jotka antavat heille pisteitä. Yrityksen korrelaatio- ja regressioanalyysiä ei tässä tapauksessa voida suorittaa lineaarisen Pearson-kertoimen perusteella. Meitä ei kiinnosta tuomarien arviointien välinen suhde. Yritysten rivit tuomarien mukaan ovat tärkeitä.
Tämän tyyppisellä analyysillä on seuraavat edut:
- Ei-parametrinen muoto suhteista tutkittujen määrien välillä.
- Helppokäyttöisyys, koska joukot voidaan osoittaa sekä nousevassa arvojärjestyksessä että alenevassa järjestyksessä.
Ainoa vaatimus tällaiselle analyysille on tarve muuntaa lähdetiedot.
Sovellusongelmat
Korrelaatio- ja regressioanalyysi perustuu seuraaviin oletuksiin:
- Havaintoja pidetään riippumattomina (viidenkertainen kotkan häviäminen ei vaikuta seuraavan kolikon käännöksen tulokseen).
- Korrelaatioanalyysissä molempia muuttujia pidetään sattumanvaraisina. Regressiossa - vain yksi (riippuvainen).
- Hypoteesia testattaessa on noudatettava normaalia jakautumista. Riippuvaisen muuttujan muutoksen tulisi olla sama jokaiselle abskissan arvolle.
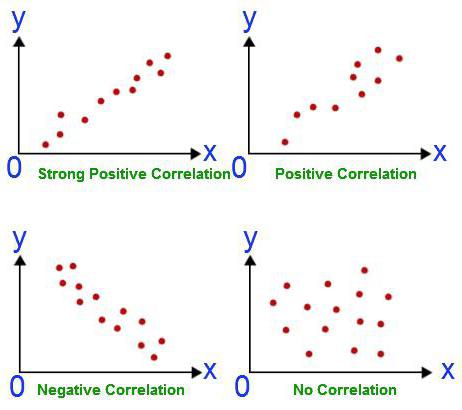
- Korrelaatiokaavio on vain ensimmäinen testi hypoteesille kahden parametrisarjan välisestä suhteesta, eikä analyysin lopputulos.
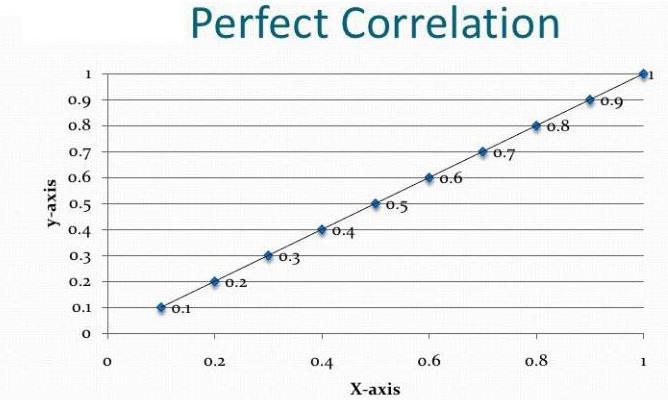
Riippuvuus ja syy
Oletetaan, että olemme laskeneet vientimäärän ja BKT: n korrelaatiokertoimen. Se osoittautui yhtäläiseksi modulo-yksikön kanssa. Olemmeko tehneet korrelaatio- ja regressioanalyysin loppuun saakka? Tietysti ei. Saatu tulos ei tarkoita ollenkaan sitä, että BKT voidaan ilmaista viennillä. Emme ole vielä osoittaneet syy-yhteyttä indikaattorien välillä. Korrelaatio-regressioanalyysi - yhden muuttujan arvojen ennustaminen toisen perusteella. Sinun on kuitenkin ymmärrettävä, että parametriin vaikuttavat usein monet tekijät. Vienti määrää BKT: n, mutta ei vain sen. On olemassa muita tekijöitä. Tässä on korrelaatio ja syy-yhteys, vaikka oikaistu bruttokansantuotteen muihin komponentteihin.
Toinen tilanne on paljon vaarallisempi. Yhdistyneessä kuningaskunnassa tehtiin kysely, joka osoitti, että lapset, joiden vanhemmat tupakoivat, olivat useammin rikollisia. Tämä johtopäätös perustuu vahvaan korrelaatioon indikaattorin välillä. Mutta onko hän oikein? Ensinnäkin riippuvuus voi olla käänteinen. Vanhemmat voivat aloittaa tupakoinnin stressin takia siitä, että heidän lapsensa ovat jatkuvasti vaikeuksissa ja rikkovat lakia. Toiseksi molemmat parametrit voivat johtua kolmannesta. Tällaiset perheet kuuluvat matalaan sosiaaliluokkaan, joille on ominaista molemmat ongelmat. Siksi korrelaation perusteella ei voida päätellä, että on olemassa syy-yhteys.
Miksi käyttää regressioanalyysiä?
Korrelaatio riippuvuus sisältää suhteiden löytämisen määrien välillä. Syy-yhteys tässä tapauksessa jää kulissien taakse. Korrelaatio- ja regressioanalyysin tehtävät osuvat vain siihen, että vahvistetaan kahden määrän arvojen välisen suhteen olemassaolo. Alun perin tutkija ei kuitenkaan kiinnitä huomiota syy-yhteyden mahdollisuuteen. Regressioanalyysillä on aina kaksi muuttujaa, joista toinen on riippuvainen. Se tapahtuu useissa vaiheissa:
- Oikean mallin valitseminen pienimmän neliösumman menetelmällä.
- Kaavan johdannainen, joka kuvaa riippumattoman muuttujan muutoksen vaikutusta toiseen.
Esimerkiksi, jos tutkimme ikän vaikutusta ihmisen kasvuun, regressioanalyysi voi auttaa ennustamaan muutoksia vuosien varrella.
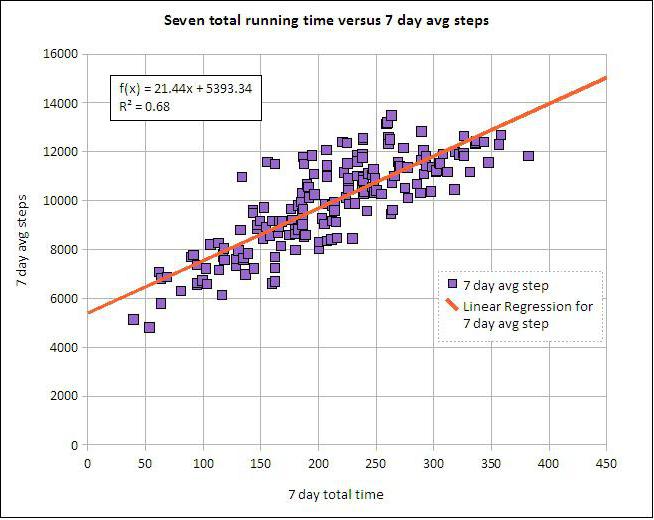
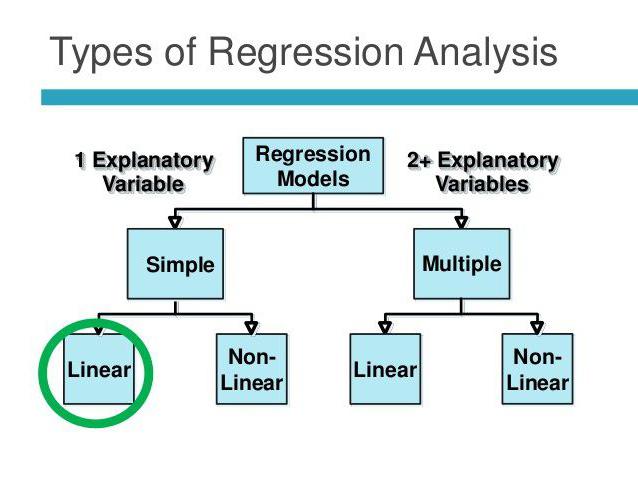
Lineaarinen ja moninkertainen regressio
Oletetaan, että X ja Y ovat kaksi toisiinsa liittyvää muuttujaa. Regressioanalyysi antaa meille mahdollisuuden ennustaa toisen suuruus toisen arvon perusteella. Esimerkiksi kypsyys ja ikä ovat riippuvaisia oireista. Niiden välinen suhde heijastuu lineaarisella regressiolla. Itse asiassa voit ilmaista X: n Y: n kautta tai päinvastoin. Mutta usein vain yksi regressioviivoista on oikea. Analyysin onnistuminen riippuu suuresti riippumattoman muuttujan oikeasta määrittämisestä. Esimerkiksi, meillä on kaksi indikaattoria: sato ja sademäärä. Jokapäiväisestä kokemuksesta käy selväksi, että ensimmäinen riippuu toisesta eikä päinvastoin.
Usean regression avulla voit laskea tuntemattoman arvon kolmen tai useamman muuttujan arvojen perusteella. Esimerkiksi riisin sato hehtaaria kohti riippuu viljan laadusta, maaperän hedelmällisyydestä, lannoitteista, lämpötilasta ja sateista. Kaikki nämä parametrit vaikuttavat kokonaistulokseen. Mallin yksinkertaistamiseksi käytetään seuraavia oletuksia:
- Itsenäisten ja vaikuttavien ominaisuuksien välinen suhde on lineaarinen.
- Monirivisyys on suljettu pois. Tämä tarkoittaa, että riippuvaisia muuttujia ei ole kytketty toisiinsa.
- Homoskedastisuus ja numerosarjojen normaliteetti.
Korrelaatio- ja regressioanalyysin käyttö
Tämän menetelmän käyttämisessä on kolme päätapausta:
- Testataan satunnaisia suhteita määrien välillä. Tässä tapauksessa tutkija määrittelee muuttujan arvot ja selvittää vaikuttavatko ne muutoksiin riippuvaisessa muuttujassa. Voit esimerkiksi antaa ihmisille erilaisia alkoholiannoksia ja mitata verenpainetta. Tässä tapauksessa tutkija tietää varmasti, että ensimmäinen on toisen syy, eikä päinvastoin. Korrelaatio-regressioanalyysi antaa sinun havaita näiden kahden muuttujan välillä suoraan verrannollinen lineaarinen suhde ja johtaa sitä kuvaava kaava. Tässä tapauksessa täysin erilaisissa mittayksiköissä ilmaistuja arvoja voidaan verrata.
- Löydä suhde kahden muuttujan välillä laajentamatta syy-yhteyttä niihin. Tässä tapauksessa ei ole eroa, minkä koon tutkija kutsuu riippuvaiseksi. Lisäksi todellisuudessa voi käydä ilmi, että kolmas muuttuja vaikuttaa niihin molempiin, joten ne muuttuvat suhteessa.
- Yhden määrän arvojen laskeminen toisen perusteella. Se perustuu yhtälöön, jossa tunnetut numerot korvataan.
Siksi korrelaatioanalyysiin sisältyy yhteyden (ei syy-yhteyden) löytäminen muuttujien välillä, ja regressioanalyysi selittää sen, usein käyttämällä matemaattista funktiota.








