Regressioanalyysi on tilastollinen menetelmä satunnaismuuttujan riippuvuuden tutkimiseksi muuttujista

Tilastollisessa mallinnuksessa regressioanalyysi on tutkimus, jota käytetään arvioimaan muuttujien välistä suhdetta. Tämä matemaattinen menetelmä sisältää monia muita menetelmiä useiden muuttujien mallintamiseksi ja analysoimiseksi, kun painopiste on riippuvaisen muuttujan ja yhden tai useamman riippumattoman suhteessa. Tarkemmin sanottuna regressioanalyysi auttaa ymmärtämään, kuinka riippuvaisen muuttujan tyypillinen arvo muuttuu, jos yksi riippumattomista muuttujista muuttuu, kun taas muut riippumattomat muuttujat pysyvät kiinteinä.

Kaikissa tapauksissa kohdeestimaatti on riippumattomien muuttujien funktio ja sitä kutsutaan regressiofunktioksi. Regressioanalyysissä on myös kiinnostavaa karakterisoida riippuvaisen muuttujan muutos regression funktiona, jota voidaan kuvata todennäköisyysjakauman avulla.

Regressioanalyysitehtävät

Tätä tilastollista tutkimusmenetelmää käytetään laajalti ennustamiseen, missä sen käytöllä on huomattava etu, mutta joskus se voi johtaa illuusioihin tai väärisiin suhteisiin, joten suositellaan sitä käytettävä huolellisesti tässä numerossa, koska esimerkiksi korrelaatio ei tarkoita syy-yhteyttä.

Regressioanalyysin suorittamiseksi on kehitetty suuri joukko menetelmiä, kuten lineaarinen ja tavallinen pienimmän neliösumman regressio, jotka ovat parametrisia. Niiden ydin on, että regressiofunktio määritetään rajallisella määrällä tuntemattomia parametreja, jotka arvioidaan datasta. Ei-parametrinen regressio antaa sen funktioiden sijaita tietyssä funktiojoukossa, jotka voivat olla äärettömässä ulottuvuudessa.

Tilastollisena tutkimusmenetelmänä regressioanalyysi riippuu käytännössä datanmuodostusprosessin muodosta ja siitä, kuinka se liittyy regressiomenetelmään. Koska dataprosessin todellinen muoto tuottaa pääsääntöisesti tuntemattoman määrän, datan regressioanalyysi riippuu usein jossain määrin tämän prosessin oletuksista. Nämä oletukset varmennetaan joskus, jos tietoja on riittävästi. Regressiomallit ovat usein hyödyllisiä, vaikka oletuksia loukataan kohtuullisesti, vaikka ne eivät pysty toimimaan maksimaalisen tehokkaasti.

Kapeammassa merkityksessä regressio voi liittyä erityisesti jatkuvien vastemuuttujien arviointiin, toisin kuin luokituksessa käytetyillä erillisillä vastemuuttujilla. Jatkuvan lähtömuuttujan tapausta kutsutaan myös metriseksi regressioksi sen erottamiseksi liittyvistä ongelmista.

Tarina

Varhaisin regression muoto on tunnettu pienimmän neliösumman menetelmä. Sen julkaisivat Legendre vuonna 1805 ja Gauss vuonna 1809. Legendre ja Gauss sovelsivat menetelmää tehtävään määrittää tähtitieteellisistä havainnoista auringon ympärillä olevien elinten kiertoradat (lähinnä komeettoja, mutta myöhemmin hiljattain löydettyjä pieniä planeettoja). Gauss julkaisi pienimmän neliösumman teorian jatkokehityksen vuonna 1821, mukaan lukien version Gauss-Markov-lauseesta.

Francis Galton loi käsitteen ”regressio” 1800-luvulla kuvaamaan biologista ilmiötä. Tärkeintä oli, että jälkeläisten kasvu esi-isien kasvusta pääsääntöisesti taantui normaaliin keskiarvoon.Galtonille regressiolla oli vain tämä biologinen merkitys, mutta myöhemmin Udney Yule ja Karl Pearson jatkoivat hänen työtään ja toivat yleisempiin tilastollisiin yhteyksiin. Yulen ja Pearsonin työssä vastemuuttujien ja selittävien muuttujien yhteistä jakautumista pidetään Gaussian. Fisher hylkäsi tämän oletuksen teoksissa 1922 ja 1925. Fisher ehdotti, että vastemuuttujan ehdollinen jakauma on Gaussin, mutta yhteisen jakauman ei pitäisi olla. Tässä suhteessa Fischerin oletus on lähempänä vuoden 1821 Gaussin muotoilua. Vuoteen 1970 asti regressioanalyysin tuloksen saaminen kesti jopa 24 tuntia.

Regressioanalyysimenetelmät ovat edelleen aktiivisen tutkimuksen alue. Viime vuosikymmeninä on kehitetty uusia menetelmiä luotettavan regression saavuttamiseksi; regressio, joka sisältää korreloivat vastaukset; regressiomenetelmät erityyppisten puuttuvien tietojen sovittamiseksi; epäparametrinen regressio; Bayesin regressiomenetelmät; regressiot, joissa ennustajamuuttujat mitataan virheellä; regressiot, joissa on enemmän ennustajia kuin havaintoja, samoin kuin syy-seuraukset regression kanssa.

Regressiomallit

Regressioanalyysimallit sisältävät seuraavat muuttujat:

• Tuntemattomat parametrit, nimeltään beeta, jotka voivat olla skalaari tai vektori.
• Riippumattomat muuttujat, X.
• Riippuvat muuttujat, Y.

Eri tieteenaloilla, joilla sovelletaan regressioanalyysiä, käytetään erilaisia ​​termejä riippuvien ja riippumattomien muuttujien sijasta, mutta kaikissa tapauksissa regressiomalli liittyy Y funktioihin X ja β.

Lähestyminen tapahtuu yleensä muodossa E (Y | X) = F (X, β). Regressioanalyysin suorittamiseksi on määritettävä funktion f tyyppi. Harvemmin se perustuu tietoon Y: n ja X: n välisestä suhteesta, jotka eivät perustu tietoihin. Jos tällaista tietoa ei ole saatavilla, valitaan joustava tai kätevä muoto F.

Riippuva muuttuja Y

Oletetaan nyt, että tuntemattomien parametrien β vektorilla on pituus k. Regressioanalyysin suorittamiseksi käyttäjän on annettava tietoja riippuvasta muuttujasta Y:

• Jos lomakkeessa (Y, X) on N tietopistettä, joissa N

• Jos tarkkaan N = K havaitaan ja funktio F on lineaarinen, niin yhtälö Y = F (X, β) voidaan ratkaista tarkasti, ei likimääräisesti. Tämä supistuu ratkaisemaan joukko N-yhtälöitä N-tuntemattomien (β-elementtien) kanssa, jolla on ainutlaatuinen ratkaisu niin kauan kuin X on lineaarisesti riippumaton. Jos F on epälineaarinen, ratkaisua ei ehkä ole olemassa tai monia ratkaisuja voi olla.
• Yleisin on tilanne, jossa N> viittaa tietoihin. Tässä tapauksessa tiedoissa on tarpeeksi tietoa arvioidakseen parhaiten tietoja vastaavan β: n ainutlaatuinen arvo, ja dataan sovellettua regressiomallia voidaan pitää β: n ylimääräisenä järjestelmänä.

Jälkimmäisessä tapauksessa regressioanalyysi tarjoaa työkalut:

• Ratkaisujen löytäminen tuntemattomille parametreille β, jotka minimoivat esimerkiksi etäisyyden mitattujen ja ennustettujen Y-arvojen välillä.
• Tietyissä tilastollisissa oletuksissa regressioanalyysi käyttää ylimääräistä tietoa tuottamaan tilastotietoja tuntemattomista parametreistä β ja riippuvaisen muuttujan Y ennustetuista arvoista.

Tarvittava lukumäärä riippumattomia mittauksia

Tarkastellaan regressiomallia, jolla on kolme tuntematonta parametria: β₀, β₁ ja p₂. Oletetaan, että kokeilija suorittaa 10 mittausta vektorin X riippumattoman muuttujan samassa arvossa.Tässä tapauksessa regressioanalyysi ei tarjoa ainutlaatuista arvojoukkoa. Paras asia, jonka voit tehdä, on arvioida riippuvaisen muuttujan Y keskiarvo ja keskihajonta. Mittaamalla kaksi erilaista X-arvoa samalla tavalla, voit saada tarpeeksi tietoa regressiota varten kahdella tuntemattomalla, mutta ei kolmella tai useammalla tuntemattomalla.

Jos kokeilijan mittaukset suoritettiin vektorin X riippumattoman muuttujan kolmella eri arvolla, regressioanalyysi antaa ainutlaatuisen arvioiden sarjan kolmelle tuntemattomalle parametrille p: ssä.

Yleisen lineaarisen regression tapauksessa yllä oleva lause vastaa vaatimusta, että matriisi X^TX on palautuva.

Tilastolliset oletukset

Kun mittausten lukumäärä N on suurempi kuin tuntemattomien parametrien k ja mittausvirheen ε määrä_minä, sitten yleensä mittausten sisältämä informaatio jaetaan sitten ja käytetään tuntemattomia parametreja koskeviin tilastollisiin ennusteisiin. Tätä tiedon ylimäärää kutsutaan regression vapauden asteeksi.

Perusoletukset

Klassisia oletuksia regressioanalyysille ovat:

• Oto edustaa päätelmäennustetta.
• Virhe on satunnaismuuttuja, jonka keskimääräinen arvo on nolla, mikä riippuu selittävistä muuttujista.
• Riippumattomat muuttujat mitataan ilman virheitä.
• Itsenäisinä muuttujina (ennustajina) ne ovat lineaarisesti riippumattomia, ts. Mitään ennustajaa ei ole mahdollista ilmaista muiden lineaarisen yhdistelmän muodossa.
• Virheet ovat korreloimattomia, ts. Diagonaalivirheiden kovarianssimatriisi ja kukin ei nolla-elementti ovat virheen varianssi.
• Virheen varianssi on havaintojen mukaan vakio (homoskedasticity). Jos ei, voit käyttää painotettujen pienimmän neliösumman menetelmää tai muita menetelmiä.

Nämä riittävät ehdot pienimmän neliösumman arvioimiseksi omaavat vaadittavat ominaisuudet, erityisesti nämä oletukset tarkoittavat, että parametriarvot ovat objektiivisia, johdonmukaisia ​​ja tehokkaita, etenkin kun ne otetaan huomioon lineaaristen arvioiden luokassa. On tärkeää huomata, että todisteet täyttävät harvoin ehdot. Eli menetelmää käytetään, vaikka oletukset eivät olisi totta. Vaihtoehtoisia oletuksia voidaan joskus käyttää mittana siitä, kuinka hyödyllinen tämä malli on. Monia näistä oletuksista voidaan lieventää edistyneemmillä menetelmillä. Tilastolliset analyysiraportit sisältävät tyypillisesti testien analyysin perustuen näytteen tietoihin ja mallin käyttökelpoisuuden menetelmiin.

Lisäksi muuttujat viittaavat joissakin tapauksissa pisteiden paikoissa mitattuihin arvoihin. Muuttujissa, jotka rikkovat tilastollisia oletuksia, voi olla paikkatrendejä ja alueellista autokorrelaatiota. Maantieteellinen painotettu regressio on ainoa menetelmä, joka käsittelee tällaisia ​​tietoja.

Lineaarinen regressioanalyysi

Lineaarisessa regressiossa piirre on, että riippuvainen muuttuja, joka on Y_minäon parametrien lineaarinen yhdistelmä. Esimerkiksi yksinkertaisessa lineaarisessa regressiossa n-pisteiden mallintamiseen käytetään yhtä riippumatonta muuttujaa x_minä, ja kaksi parametria, p₀ ja p₁.

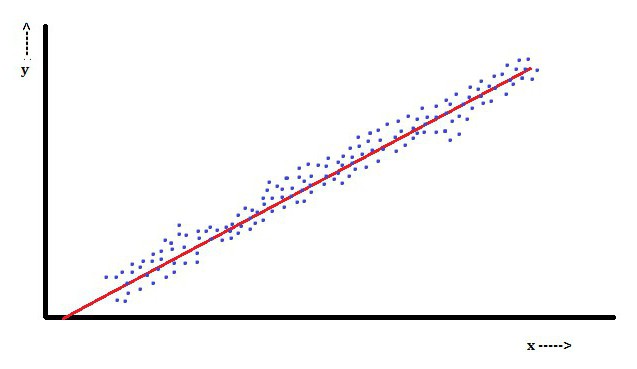
Usealla lineaarisella regressiolla on useita riippumattomia muuttujia tai niiden funktioita.

Satunnaisella näytteenotolla populaatiosta sen parametrit antavat mahdollisuuden saada esimerkki lineaarisesta regressiomallista.

Tässä suhteessa pienimmän neliösumman menetelmä on suosituin. Sitä käyttämällä saadaan parametriarvioita, jotka minimoivat neliömäisten jäännösten summan. Tällainen tämän funktion minimointi (joka on ominaista lineaariselle regressiolle) johtaa joukkoon normaaleja yhtälöitä ja joukko lineaarisia yhtälöitä parametreilla, jotka ratkaistaan ​​parametriarvioiden saamiseksi.

Lisäksi olettaen, että populaation virhe yleensä leviää, tutkija voi käyttää näitä standardivirheiden arvioita luotettavuusvälien luomiseen ja testihypoteesien tekemiseen sen parametreista.

Epälineaarinen regressioanalyysi

Esimerkki, jossa funktio ei ole lineaarinen parametrien suhteen, osoittaa, että neliöiden summa tulisi minimoida käyttämällä iteratiivista menettelyä. Tämä tuo mukanaan monia komplikaatioita, jotka määräävät erot lineaaristen ja epälineaaristen pienimmän neliösumman menetelmien välillä. Tämän seurauksena epälineaarista menetelmää käyttävän regressioanalyysin tulokset ovat joskus arvaamattomia.

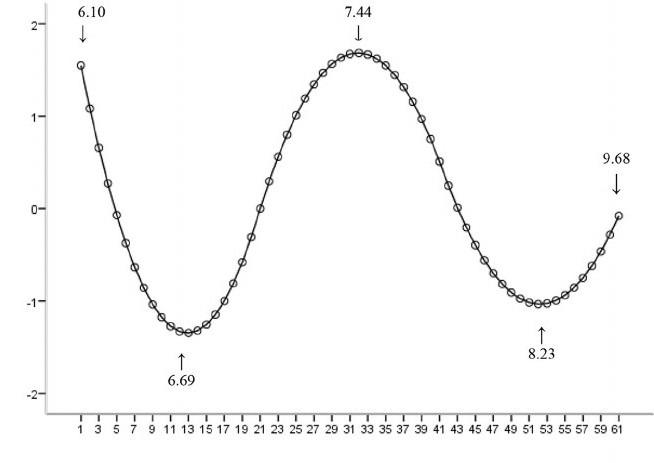
Tehon ja näytteen koon laskeminen

Tässä ei yleensä ole yhdenmukaisia ​​menetelmiä havaintojen lukumäärään verrattuna mallin riippumattomien muuttujien lukumäärään. Ensimmäisen säännön ehdottivat Good ja Hardin, ja se näyttää N = t ^ n, jossa N on näytteen koko, n on riippumattomien muuttujien lukumäärä ja t on toivottujen tarkkuuksien saavuttamiseksi tarvittavien havaintojen lukumäärä, jos mallissa oli vain yksi riippumaton muuttuja. Esimerkiksi tutkija rakentaa lineaarisen regressiomallin käyttämällä tietojoukkoa, joka sisältää 1000 potilasta (N). Jos tutkija päättää, että viivan (m) tarkkaan määrittämiseen tarvitaan viisi havaintoa, niin mallin tukemien riippumattomien muuttujien enimmäismäärä on 4.

Muut menetelmät

Huolimatta siitä, että regressiomallin parametrit arvioidaan yleensä pienimmän neliösumman menetelmällä, on muitakin menetelmiä, joita käytetään paljon harvemmin. Esimerkiksi nämä ovat seuraavat menetelmät:

• Bayesin menetelmät (esim. Bayesin lineaarisen regression menetelmä).
• Prosentti regressio, käytetään tilanteissa, joissa virheiden vähentämistä pidetään tarkoituksenmukaisempana.
• Pienimmät absoluuttiset poikkeamat, mikä on vakaampaa kvantiilen regressioon johtavien poikkeamien läsnäollessa.
• Ei-parametrinen regressio, joka vaatii suuren määrän havaintoja ja laskelmia.
• Oppimittarin etäisyys, jota tutkitaan etsittäessä merkitsevää metristä etäisyyttä tietyssä syöttötilassa.

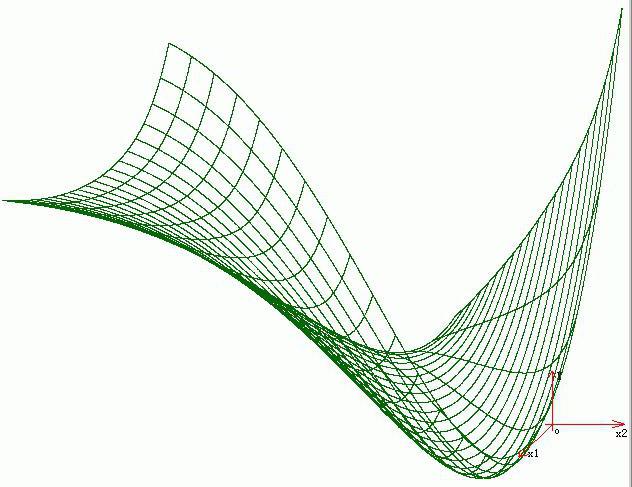
ohjelmistot

Kaikki tärkeimmät tilastolliset ohjelmistopaketit suoritetaan käyttämällä pienimmän neliösumman regressioanalyysiä. Yksinkertaista lineaarista regressiota ja useita regressioanalyysejä voidaan käyttää joissain laskentataulukkosovelluksissa, samoin kuin joissakin laskimissa. Vaikka monet tilastolliset ohjelmistopaketit voivat suorittaa erityyppisiä epäparametrisia ja luotettavia regressioita, nämä menetelmät ovat vähemmän standardisoituja; Eri ohjelmistopaketit toteuttavat erilaisia ​​menetelmiä. Erikoistunut regressio-ohjelmisto on kehitetty käytettäväksi esimerkiksi tutkimusanalyysissä ja neurokuvauksessa.