Monimuuttujavarianssianalyysi

Varianssianalyysi on joukko tilastollisia menetelmiä, jotka on suunniteltu testaamaan hypoteesit tiettyjen merkkien ja tutkittavien tekijöiden välisestä suhteesta, joilla ei ole kvantitatiivista kuvausta, sekä määrittämään tekijöiden vaikutusaste ja niiden vuorovaikutus. Erikoiskirjallisuudessa sitä kutsutaan usein ANOVAksi (englanninkielisestä nimestä Analysis of Variation). Tätä menetelmää kehitti ensimmäisen kerran R. Fisher vuonna 1925.

Varianssianalyysityypit ja -kriteerit

Tätä menetelmää käytetään tutkimaan kvalitatiivisten (nimellisten) ominaisuuksien ja kvantitatiivisen (jatkuvan) muuttujan välistä suhdetta. Itse asiassa hän testaa hypoteesia, jonka mukaan useiden näytteiden aritmeettinen keskiarvo on sama. Sitä voidaan siis pitää parametrisena kriteerinä vertaamalla useiden näytteiden keskipisteitä kerralla. Jos käytät tätä menetelmää kahdelle näytteelle, varianssianalyysin tulokset ovat identtisiä t-opiskelijan testin tulosten kanssa. Toisin kuin muut kriteerit, tämän tutkimuksen avulla voimme kuitenkin tutkia ongelmaa yksityiskohtaisemmin.

Tilastojen varianssianalyysi perustuu lakiin: Yhdistetyn näytteen poikkeamien neliöiden summa on yhtä suuri kuin ryhmän sisäisten poikkeamien neliöiden ja ryhmien välisten poikkeamien neliöiden summa. Tutkimuksessa Fisher-testiä käytetään määrittämään ryhmien välisten varianssien eron merkitys ryhmän sisäisistä variansseista. Tätä varten välttämättömät edellytykset ovat näytteiden normaali jakautuminen ja homoskedasticity (varianssien yhtäläisyys). Erota yhden ulottuvuuden (yksimuuttuja) varianssianalyysi ja monimuuttuja (monimuuttuja). Ensimmäinen tarkastelee tutkitun määrän riippuvuutta yhdestä ominaisuudesta, toinen - välittömästi monista, ja antaa myös mahdollisuuden tunnistaa niiden välinen suhde.

tekijät

Tekijöitä kutsutaan hallituiksi olosuhteiksi, jotka vaikuttavat lopputulokseen. Sen tasoa tai prosessointimenetelmää kutsutaan arvoksi, joka kuvaa tämän tilan erityistä ilmenemismuotoa. Nämä numerot annetaan yleensä nimellis- tai sarja-asteikolla. Usein lähtöarvot mitataan kvantitatiivisella tai ordinaalisella asteikolla. Sitten syntyy ongelma lähtötietojen ryhmittämisessä havaintojen sarjaan, joka vastaa suunnilleen samoja numeerisia arvoja. Jos ryhmien lukumäärän katsotaan olevan liian suuri, niin havaintojen lukumäärä niissä voi olla riittämätön luotettavien tulosten saamiseksi. Jos otat numeron liian pieneksi, tämä voi johtaa siihen, että järjestelmään kohdistuvat vaikutukset häviävät merkittävästi. Tietynlainen tapa ryhmitellä riippuu arvojen muutoksen määrästä ja luonteesta. Jaksojen lukumäärä ja koko yksisuuntaisessa analyysissä määritetään useimmiten yhtäläisten intervallien periaatteella tai yhtäläisten taajuuksien periaatteella.

Varianssi-ongelmien analyysi

Joten, on tapauksia, joissa joudut vertaamaan kahta tai useampaa näytettä. Silloin on suositeltavaa käyttää varianssianalyysiä. Menetelmän nimi osoittaa, että varianssin komponenttien tutkimuksesta tehdään johtopäätöksiä. Tutkimuksen ydin on, että indikaattorin yleinen muutos on jaettu osiin, jotka vastaavat kunkin yksittäisen tekijän vaikutusta. Harkitse useita ongelmia, jotka tyypillinen varianssianalyysi ratkaisee.

Esimerkki 1

Työpajassa on useita työstökoneita - automaattiset koneet, jotka tuottavat tietyn osan. Kunkin osan koko on satunnainen arvo, joka riippuu kunkin koneen asetuksista ja osien valmistuksen aikana tapahtuvista satunnaispoikkeamista.On tarpeen selvittää, onko koneet yhtä hyvin konfiguroitu osien mittojen mittojen mukaan.

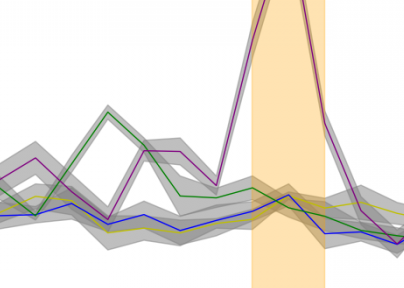
Esimerkki 2

Sähkölaitteiden valmistuksen aikana käytetään erityyppisiä eristepapereita: jäähdytin, sähköinen jne. Laite voidaan kyllästää erilaisilla aineilla: epoksihartsilla, lakalla, ML-2-hartsilla jne. Vuodot voidaan poistaa tyhjiössä korkeassa paineessa kuumentamalla. Se voidaan kyllästää upottamalla lakkaan, jatkuvan lakkavirran alla jne. Sähkölaite kokonaisuudessaan kaadetaan tietyllä yhdisteellä, jota on useita vaihtoehtoja. Laatuindikaattorit ovat eristyksen dielektrinen lujuus, käämin ylikuumenemisen lämpötila toimintatilassa ja monet muut. Laitteiden valmistusprosessin testaamisen aikana on tarpeen määrittää, kuinka kukin luetelluista tekijöistä vaikuttaa laitteen suorituskykyyn.

Esimerkki 3

Vaunuvaunu palvelee useita vaunun reittejä. Eri tyyppiset johdinautot työskentelevät heidän hyväkseen, ja hintakeruun kerää 125 ohjaajaa. Varaston johto on kiinnostunut kysymyksestä: miten verrata kunkin ohjaimen taloudellista suorituskykyä (tuloja) ottaen huomioon eri reitit, erityyppiset vaunubussit? Kuinka määrittää tietyntyyppisen vaunun taloudellisen toteuttamiskelpoisuuden tietylle reitille? Kuinka asettaa kohtuulliset vaatimukset tulon määrälle, jonka kapellimestari tuottaa jokaiselle reitille erityyppisissä vaunubusseissa?

Menetelmän valitsemisen tehtävänä on, kuinka saada mahdollisimman paljon tietoa vaikutuksesta kunkin tekijän lopputulokseen, määrittää tällaisen vaikutuksen numeeriset ominaisuudet, niiden luotettavuus alimmalla kustannuksella ja mahdollisimman lyhyessä ajassa. Tällaiset ongelmat voidaan ratkaista analysoimalla varianssimenetelmiä.

Yksisuuntainen analyysi

Tutkimuksen tavoitteena on arvioida tietyn tapauksen vaikutuksen suuruutta analysoidussa katsauksessa. Toinen yksisuuntaisen analyysin tehtävä voi olla kahden tai useamman olosuhteen vertailu keskenään niiden vaikutuksen eroamisen määrittämiseksi. Jos nollahypoteesi hylätään, seuraava askel on saatujen ominaisuuksien kvantitatiivinen arviointi ja luottamusvälien muodostaminen. Jos nolla hypoteesi sitä ei voida hylätä, se yleensä hyväksytään ja vaikutusten olemuksesta tehdään johtopäätös.

Yhden variaattorin varianssianalyysistä voi tulla ei-parametrinen analogi Kraskel-Wallis -järjestysmenetelmälle. Sitä kehittivät amerikkalainen matemaatikko William Kraskel ja taloustieteilijä Wilson Wallis vuonna 1952. Tämä peruste määritettiin testaamaan nollahypoteesi, jonka mukaan vaikutukset tutkituihin näytteisiin ovat yhtä suuret kuin tuntemattomat, mutta yhtä suuret keskiarvot. Näytteiden lukumäärän tulisi olla enemmän kuin kaksi.

Jonkhier-kriteerin (Jonkhier-Terpstra) ehdottivat itsenäisesti hollantilainen matemaatikko T.J. Terpstrom vuonna 1952 ja brittiläinen psykologi E. R. Jonkhier vuonna 1954. Sitä käytetään, kun on etukäteen tiedossa, että käytettävissä olevat tuloryhmät tilasivat tutkitun tekijän vaikutuksen kasvu, joka mitataan ordinaalisella asteikolla.

M - brittiläisen tilastotieteilijän Maurice Stevenson Bartlettin vuonna 1937 ehdottamaa Bartlett-testiä käytetään nollahypoteesin testaamiseen, joka koskee useiden normaalien yleispopulaatioiden yhtäläisyyksiä, joista tutkitut näytteet on otettu, ja joilla on yleensä eri tilavuudet (kunkin näytteen tulee olla vähintään neljä ).

G on Cochren-testi, jonka amerikkalainen William Gemmel Cochren löysi vuonna 1941. Sitä käytetään nollahypoteesin testaamiseen, jonka mukaan normaalien yleispopulaatioiden varianssit ovat yhtä suuret riippumattomien, saman tilavuuden näytteiden suhteen.

Ei-parametrinen Levene-kriteeri, jonka amerikkalainen matemaatikko Howard Levene ehdotti vuonna 1960, on vaihtoehto Bartlett-kriteerille olosuhteissa, joissa ei ole varmuutta siitä, että tutkitut näytteet noudattavat normaalia jakaumaa.

Amerikkalaiset tilastotieteilijät Morton B. Brown ja Alan B. Forsyth ehdottivat vuonna 1974 testiä (Brown-Forsythe-kriteeri), joka eroaa jonkin verran Leuven-kriteeristä.

Kahden tekijän analyysi

Kytkettyihin normaalijakautuneisiin näytteisiin käytetään kaksisuuntaista varianssianalyysiä. Käytännössä käytetään usein tämän menetelmän monimutkaisia ​​taulukoita, erityisesti niitä, joissa jokainen solu sisältää kiinteän tason arvoja vastaavan datajoukon (toistuvat mittaukset). Jos kaksisuuntaisen varianssianalyysin soveltamiseksi tarvittavat oletukset eivät täyty, käytetään amerikkalaisen taloustieteilijän Milton Friedmanin vuoden 1930 lopulla kehittämää ei-parametrista Friedman-sijoituskriteeriä (Friedman, Kendall ja Smith), joka on riippumaton jakauman tyypistä.

Oletetaan vain, että määrien jakauma on sama ja jatkuva ja että ne ovat toisistaan ​​riippumattomia. Null-hypoteesia testattaessa tulos esitetään suorakulmaisen matriisin muodossa, jossa rivit vastaavat tekijä B: n tasoja ja sarakkeet vastaavat A: n tasoja. Jokainen taulukon solu (lohko) voi olla tulosta mittaamalla parametreja yhdestä objektista tai objektiryhmästä molempien tekijöiden tasojen vakioarvoilla. . Tässä tapauksessa vastaava tieto toimitetaan tietyn parametrin keskiarvoina kaikille tutkitun näytteen mittauksille tai kohteille. Lähtödatan kriteerin soveltamiseksi on tarpeen siirtyä suorista mittaustuloksista niiden sijoitukseen. Sijoitus suoritetaan jokaiselle riville erikseen, ts. Arvot tilataan jokaiselle kiinteälle arvolle.

Sivukriteeri (L-kriteeri), jonka amerikkalainen tilastotieteilijä E. B. Page ehdotti vuonna 1963, on tarkoitettu nollahypoteesin testaamiseen. Suurissa näytteissä käytetään sivun lähentämistä. Ne, noudattaen vastaavien nollahypoteesien todellisuutta, noudattavat normaalia normaalijakaumaa. Jos lähdetaulukon riveillä on samat arvot, on käytettävä keskiarvoja. Lisäksi päätelmien tarkkuus on huonompi, sitä enemmän on samanlaisia ​​sattumia.

Q on V. Cohrenin vuonna 1937 ehdottama Cochren-kriteeri. Sitä käytetään tapauksissa, joissa homogeenisten kohteiden ryhmät altistuvat useammalle kuin kahdelle ja joille on mahdollista saada kaksi vastausta - ehdollisesti negatiivinen (0) ja ehdollisesti positiivinen (1) . Nollahypoteesi koostuu samanlaisista vaikutusvaikutuksista. Kaksisuuntainen varianssianalyysi mahdollistaa prosessointiefektien olemassaolon määrittämisen, mutta ei mahdollista sen määrittämistä, joille sarakkeille tämä vaikutus on olemassa. Tämän ongelman ratkaisemiseksi käytetään useiden Sheffe-yhtälöiden menetelmää kytketyille näytteille.

Monimuuttuja-analyysi

Monimuuttujavarianssianalyysin tehtävä syntyy, kun on tarpeen määrittää kahden tai useamman olosuhteen vaikutus tiettyyn satunnaismuuttujaan. Tutkimuksessa esitetään yhden riippuvan satunnaismuuttujan, mitattuna ero- tai suhteellisuusasteikolla, ja useiden riippumattomien muuttujien esiintyminen, joista kukin ilmaistaan ​​nimelliskaalassa tai sijoitusjärjestyksessä. Varianssitietojen analysointi on melko kehittynyt osa matemaattisia tilastoja, jolla on paljon vaihtoehtoja. Tutkimuskonsepti on yhteinen sekä yksitekijälle että monitekijälle. Sen ydin on, että kokonaisvarianssi on jaettu komponentteihin, mikä vastaa tiettyä tietoryhmää. Jokaisella tietoryhmällä on oma malli.Tässä tarkastellaan vain perussäännöksiä, jotka ovat tarpeen sen laajimmin käytettyjen vaihtoehtojen ymmärtämiseksi ja käytännön hyödyntämiseksi.

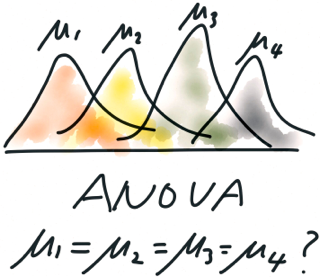
Tekijöiden varianssianalyysi vaatii melko huolellista suhtautumista syöttötietojen keräämiseen ja esittämiseen ja etenkin tulosten tulkintaan. Toisin kuin yksikerroinen, jonka tulokset voidaan mielivaltaisesti sijoittaa tiettyyn sekvenssiin, kaksikerroiset tulokset vaativat monimutkaisemman esityksen. Vielä vaikeampi tilanne syntyy, kun olosuhteita on kolme, neljä tai enemmän. Tämän vuoksi enemmän kuin kolme (neljä) ehtoa sisällytetään harvoin malliin. Esimerkki on resonanssin esiintyminen tietyllä sähköympyrän kapasitanssin ja induktanssin arvossa; kemiallisen reaktion esiintyminen tietyillä elementtijoukkoilla, joista järjestelmä rakennetaan; poikkeavien vaikutusten esiintyminen monimutkaisissa järjestelmissä tietyllä olosuhteiden sattumalla. Vuorovaikutuksen läsnäolo voi perustavanlaatuisesti muuttaa järjestelmän mallia ja joskus johtaa kokeilijan tekemisissä olevien ilmiöiden luonteen uudelleen ajatteluun.

Monimuuttujavarianssianalyysi toistuvilla kokeilla

Mittaustiedot voidaan usein ryhmitellä ei kahteen, vaan suurempiin tekijöihin. Joten jos pidämme trolibussirenkaiden renkaiden käyttöiän varianssianalyysin ottaen huomioon olosuhteet (valmistaja ja renkaiden käyttöreitti), voimme erottaa renkaan käyttökauden (nimittäin talvi- ja kesäkäytön) erillisenä ehtona. Seurauksena on, että meillä on kolme tekijän menetelmä.

Jos olosuhteita on enemmän, lähestymistapa on sama kuin kaksifaktorisessa analyysissä. Kaikissa tapauksissa he yrittävät yksinkertaistaa mallia. Kahden tekijän vuorovaikutuksen ilmiö ei ilmene niin usein, ja kolmoisvuorovaikutus tapahtuu vain poikkeustapauksissa. Ne sisältävät vuorovaikutuksen, josta on aikaisempaa tietoa, ja hyvät syyt sen huomioon ottamiseksi mallissa. Yksittäisten tekijöiden eristämisprosessi ja niiden huomioon ottaminen on suhteellisen yksinkertaista. Siksi usein halutaan tuoda esiin enemmän olosuhteita. Tätä ei pidä viedä pois. Mitä enemmän ehtoja, sitä vähemmän luotettavasta mallista tulee ja sitä suurempi virheen todennäköisyys. Itse malli, joka sisältää suuren määrän riippumattomia muuttujia, tulee tarpeeksi vaikeaksi tulkitavana ja hankalaksi käytännöllisessä käytössä.

Yleinen idea varianssianalyysistä

Tilastojen varianssianalyysi on menetelmä, jolla saadaan havainnoista tulokset, jotka ovat riippuvaisia ​​useista samanaikaisesti olemassa olevista olosuhteista, ja arvioida niiden vaikutuksia. Kontrolloitua muuttujaa, joka vastaa menetelmää vaikuttaa tutkittavaan kohteeseen ja tietyssä ajassa saavuttaa tietyn arvon, kutsutaan tekijäksi. Ne voivat olla laadullisia ja määrällisiä. Määrällisten olosuhteiden tasot saavat tietyn arvon numeerisella asteikolla. Esimerkkejä ovat lämpötila, paine, aineen määrä. Laadulliset tekijät ovat eri aineet, erilaiset teknologiset menetelmät, laitteet, täyteaineet. Niiden tasot vastaavat nimien mittakaavaa.

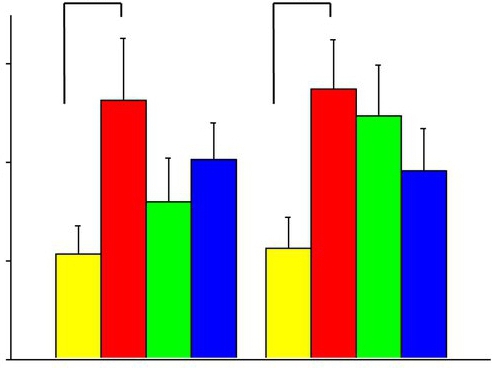
Laatu voi sisältää myös pakkausmateriaalin tyypin, annosmuodon säilytysolosuhteet. On myös järkevää määrittää raaka-aineiden jauhatusaste, rakeiden fraktiokoostumus, jolla on määrällinen merkitys, mutta jota on vaikea hallita, jos käytetään kvantitatiivista asteikkoa. Laatukertoimien lukumäärä riippuu annosmuodon tyypistä sekä lääkeaineiden fysikaalisista ja teknologisista ominaisuuksista. Esimerkiksi tabletteja voidaan saada kiteisistä aineista suoraan puristamalla. Tällöin riittää valinta liuku- ja voiteluaineiksi.

Esimerkkejä laadullisista tekijöistä erityyppisille annosmuodoille

• Tinktuurat. Uutteen koostumus, uuttolaji, raaka-aineiden valmistusmenetelmä, valmistusmenetelmä, suodatusmenetelmä.
• Uutteet (nestemäiset, paksut, kuivat). Uutteen koostumus, uuttamismenetelmä, asennustyyppi, uuttoaineen ja painolastiaineiden poistomenetelmä.
• Tablettia. Apuaineiden, täyteaineiden, hajotusaineiden, sideaineiden, voiteluaineiden ja liukastusaineiden koostumus. Menetelmä tablettien tuottamiseksi, käsittelylaitteen tyyppi. Kuoren tyyppi ja sen komponentit, kalvonmuodostajat, pigmentit, väriaineet, pehmittimet, liuottimet.
• Injektioliuokset. Liuottimen tyyppi, suodatusmenetelmä, stabilointiaineiden ja säilöntäaineiden luonne, sterilointiolosuhteet, ampullien täyttömenetelmä.
• Peräpuikkoina. Peräpuikkojen koostumus, menetelmä peräpuikkojen, täyteaineiden ja pakkausten valmistamiseksi.
• Voidetta. Pohjan koostumus, rakenneosat, voiteen valmistusmenetelmä, välineet, pakkaus.
• Kapselia. Vaippamateriaalin tyyppi, kapselien valmistusmenetelmä, pehmittimen tyyppi, säilöntäaine, väriaine.
• Liniments. Valmistusmenetelmä, koostumus, välineiden tyyppi, emulgaattorityyppi.
• Jousitus. Liuottimen tyyppi, stabilointiaineen tyyppi, dispergointimenetelmä.

Esimerkkejä tablettien valmistusprosessissa tutkituista laadullisista tekijöistä ja niiden tasoista

• Leivinjauhe. Perunatärkkelys, valkoinen savi, natriumbikarbonaatin ja sitruunahapon seos, emäksinen magnesiumkarbonaatti.
• Sitova liuos. Vesi, tärkkelyspasta, sokerisiirappi, metyyliselluloosaliuos, hydroksipropyylimetyyliselluloosaliuos, polyvinyylipyrrolidoniliuos, polyvinyylialkoholiliuos.
• Liukuaine. Aerosil, tärkkelys, talkki.
• Täyteainetta. Sokeri, glukoosi, laktoosi, natriumkloridi, kalsiumfosfaatti.
• Voiteluainetta. Steariinihappo, polyetyleeniglykoli, parafiini.

Varianssimallien analyysi tutkittaessa valtion kilpailukykyä

Yksi tärkeimmistä valtion tilan arviointiperusteista, joiden avulla arvioidaan sen hyvinvoinnin ja sosioekonomisen kehityksen tasoa, on kilpailukyky, ts. Kansantaloudelle ominainen ominaisuusjoukko, joka määrittelee valtion kyvyn kilpailla muiden maiden kanssa. Kun olemme määrittäneet valtion paikan ja roolin globaaleilla markkinoilla, voimme laatia selkeän strategian sen varmistamiseksi taloudellinen turvallisuus kansainvälisesti, koska se on avain positiivisiin suhteisiin Venäjän ja kaikkien maailmanmarkkinoiden toimijoiden välillä: sijoittajat, velkojat, osavaltioiden hallitukset.

Maiden kilpailukyvyn tason vertailemiseksi maat sijoitetaan monimutkaisten indeksien avulla, jotka sisältävät erilaisia ​​painotettuja indikaattoreita. Näiden indeksien perustana ovat keskeiset tekijät, jotka vaikuttavat taloudelliseen, poliittiseen jne. Tilanteeseen. Sarja malleja valtion kilpailukyvyn tutkimiseksi tarjoaa monimuuttujaisten tilastollisten analyysimenetelmien käytön (erityisesti varianssianalyysi (tilastot), ekonometrinen mallinnus, päätöksenteko) ja sisältää seuraavat päävaiheet:

1. Indikaattorien ja indikaattorien järjestelmän muodostaminen.
2. Valtion kilpailukyvyn indikaattorien arviointi ja ennustaminen.
3. Valtioiden kilpailukyvyn indikaattorien ja indikaattorien vertailu.

Tarkastellaan nyt tämän kompleksin kunkin vaiheen mallien sisältöä.

Ensimmäisessä vaiheessa Asiantuntijamenetelmien avulla muodostetaan perusteltu joukko taloudellisia indikaattoreita -indikaattoreita valtion kilpailukyvyn arvioimiseksi ottaen huomioon sen kehityksen erityispiirteet, jotka perustuvat kansainvälisiin luokituksiin ja tilasto-osastojen tietoihin, jotka heijastavat järjestelmän kokonaisuutta ja sen prosesseja.Näiden indikaattorien valinta on perusteltua tarpeella valita ne, jotka käytännön näkökulmasta parhaiten mahdollistavat valtion tason, sen sijoituskohteiden houkuttelevuuden ja olemassa olevien potentiaalisten ja tosielämäuhkien suhteellisen lokalisoinnin mahdollisuuksien määrittämisen.

Kansainvälisten luokitusjärjestelmien pääindikaattorit-indikaattorit ovat indeksit:

1. Globaali kilpailukyky (HVK).
2. Taloudellinen vapaus (IES).
3. Ihmisen kehitys (HDI).
4. Korruption käsitykset (CPI).
5. Sisäiset ja ulkoiset uhat.
6. Kansainvälisen vaikutusvallan (IPMV) potentiaali.

Toinen vaihe Se tarjoaa valtion kilpailukyvyn indikaattorien arvioinnin ja ennustamisen tutkittujen 139 maailman maan kansainvälisten luokitusten perusteella.

Kolmas vaihe tarjoaa vertailun valtioiden kilpailukyvyn ehdoista menetelmiä käyttämällä korrelaatio- ja regressioanalyysi.

Tutkimuksen tuloksia käyttämällä on mahdollista määrittää prosessien luonne kokonaisuutena ja valtion kilpailukyvyn yksittäisistä komponenteista; Testaa hypoteesi tekijöiden vaikutuksesta ja niiden suhteesta soveltuvaan merkitsevyystaso.

Ehdotetun mallisarjan toteuttaminen antaa paitsi arvioida valtioiden kilpailukyvyn ja investointien houkuttelevuuden nykytilannetta myös analysoida johtamisen heikkouksia, estää virheellisissä päätöksissä tapahtuvia virheitä ja estää kriisin kehittymisen valtiossa.