A "sztochasztikus" egy olyan szó, amelyet a fizikusok, a matematikusok és más tudósok használnak a véletlenszerű folyamatok leírására. Eredete az ókori görög. Lefordítva azt jelenti, hogy "képes kitalálni".
A „sztochasztikus” szó jelentése

A "sztochasztikus" olyan fogalom, amelyet a tudomány számos különféle területén használnak. Valami véletlenszerűségét, véletlenszerűségét, bizonytalanságát jelenti. Arisztotelész etikájában (szobrászati portréját fentebb mutatjuk be) a „sztochasztikus” fogalma olyan meghatározás, amely utal a képességre. A matematikusok nyilvánvalóan azon az alapon használták, hogy a véletlen elem csak akkor jelenik meg, amikor kitalálni szükséges. A "sztochasztikus" kifejezés olyan fogalom, amelyet az Új Nemzetközi Szótárban "feltételezés" -ként határoznak meg.
Így meg lehet jegyezni, hogy ennek a fogalomnak a technikai jelentése nem pontosan felel meg szókincsének (lexikális) jelentésének. Egyes szerzők a "sztochasztikus folyamat" kifejezést használják a "véletlenszerű folyamat" szinonimájaként.
Sztochaszticitás a matematikában

Ennek a kifejezésnek a használata a matematikában jelenleg széles körben elterjedt. Például a valószínűségi elméletben létezik olyan koncepció, mint a sztochasztikus folyamat. Ennek eredményét nem tudja meghatározni a rendszer kezdeti állapota.
A "sztochaszticitás" fogalmának a matematikában való felhasználását Vladislav Bortskevich munkáinak tulajdonítják. Ő volt az, aki a kifejezést a "hipotézisek előterjesztése" értelmében használja. A matematikában, különösen a tudomány olyan részében, mint a valószínűségi elmélet, a véletlenszerű kutatás területe fontos szerepet játszik. Van például olyan dolog, mint egy sztochasztikus mátrix. Ennek a mátrixnak az oszlopai vagy sorai összeadódnak.
Sztochasztikus matematika (pénzügyi)
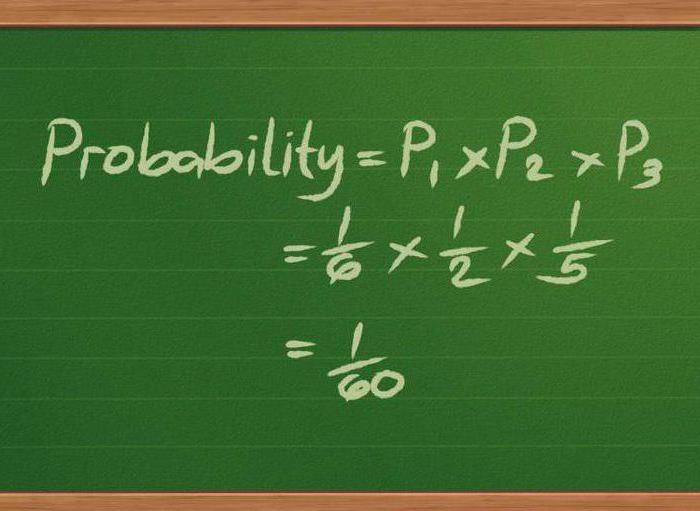
A matematika ezen szakasza a bizonytalansági körülmények között működő pénzügyi struktúrákat elemzi. Úgy tervezték, hogy megtalálják a pénzügyi eszközök és struktúrák kezelésének legésszerűbb módszereit, figyelembe véve például a sztochasztikus fejlődést, a kockázatot, az időt stb.
A tudományban szokás megkülönböztetni a következő szerkezeteket és objektumokat, amelyeket a pénzügyi matematika egészében használnak:
- cégek (például cégek);
- egyének
- közvetítő struktúrák (nyugdíjalapok, bankok);
- pénzügyi piacok.
A sztochasztikus pénzügyi matematika tanulmányozásának fő célja pontosan az utóbbi. Ez a szakasz olyan tudományágakon alapul, mint a véletlen folyamatok statisztikája, a véletlen folyamatok elmélete stb.
Jelenleg, még a tudománytól távol eső emberektől is, számos sajtóban és a sajtóban megjelenő publikációból ismert, hogy az úgynevezett globális pénzügyi indexek (például a Dow Jones index) értékei a részvényárak véletlenszerűen változnak. L. Bachelier először megkísérelte a részvényárak alakulását a matematika segítségével leírni. Sztochasztikus módszere a valószínűségi elméletre épül. Ezt a kísérletet bemutató L. Bachelier disszertáció 1900-ban jelent meg. A tudós bebizonyította a jelenleg a vételi opciók valós érték formulaként ismert képletet. Ez a sztochasztikus valószínűséget tükrözi.
Fontos ötleteket, amelyek később eredményes piaci elmélet kialakulásához vezettek, M. Kendall 1953-ban kiadott munkája ismertette. Ez a cikk a részvényárfolyam-dinamika kérdésével foglalkozik. A kutató sztochasztikus folyamatokkal írja le.
Sztochaszticitás a fizikában
Köszönet a fizikusoknak E. Fermi, S. Ulam, N. Metropolis és D.A Neumann általánosan használt Monte Carlo módszer. A neve egy kaszinóból származik, amely ugyanabban a városban található egy országban, mint például Monaco. Itt volt az, hogy Ulam bácsi kölcsönvett pénzt a játékért. Az ismétlés és az esély jellege a folyamatok tanulmányozásához hasonló ahhoz, ami a kaszinóban történik.

E modellezési módszer alkalmazásakor először egy valószínűségi analógot keresnek. Ezt megelőzően a modellezést ellentétes irányban hajtották végre: a korábban kapott determinisztikus probléma eredményének ellenőrzésére használták. Bár hasonló megközelítések léteztek a Monte Carlo-módszer felfedezése előtt, nem voltak népszerűek és általánosak.
Enrico Fermi 1930-ban sztochasztikus módszereket alkalmazott a neutron tulajdonságainak kiszámításához, amelyeket csak akkor fedeztek fel. A Monte Carlo módszereket később a Manhattan-projekten dolgoztak, bár akkoriban a számítógépek képességei szignifikánsan korlátozottak voltak. Ezért csak a számítógépek megjelenése után váltak elterjedté.
Sztochasztikus jelek
A szokásos és sztochasztikus jelek eltérő hullámformákkal rendelkeznek. Ha utóbbit újra megmérjük, akkor olyan oszcillációkat kapunk, amelyek új formája eltér az előzőtől, de bizonyos hasonlóságot mutat az alapvető jellemzőkben. A sztochasztikus jelre példa a tengeri hullámok oszcillációinak rögzítése.
Miért kell beszélni ezekről a meglehetősen szokatlan jelekről? A tény az, hogy az automatikus rendszerek tanulmányozásában még általánosabbak, mint amire számítottak.
Sztochaszticitás és mesterséges intelligencia
A sztochasztikus mesterséges intelligencia programok valószínűségi módszerekkel működnek. Példaként említhetők az algoritmusok, például a sztochasztikus optimalizálás vagy az idegi hálózatok. Ugyanez vonatkozik a szimulált lágyítási és genetikai algoritmusokra. Ezekben az esetekben a sztochaszticitás a problémában önmagában vagy valami bizonytalanság körülményeinek megtervezésében rejlik. A modellező szer determinisztikus környezete egyszerűbb, mint sztochasztikus.

Tehát, amint látjuk, a számunkra érdeklődés fogalmát a tudomány sok területén használják. Csak felsoroltuk és jellemeztük alkalmazásának fő területeit. Mindezen folyamatok vizsgálata, láthatja, nagyon fontos és releváns. Ezért valószínűleg hosszú ideje használjuk a számunkra érdeklődő fogalmat a tudományban.








