A statisztikai szignifikancia szintje fontos mutató, amely tükrözi a kapott (előrejelzett) adatok pontosságába és valódiságába vetett bizalom mértékét. A fogalmat széles körben használják különféle területeken: a szociológiai kutatások elvégzésétől a tudományos hipotézisek statisztikai teszteléséig.

meghatározás
A statisztikai szignifikancia (vagy statisztikailag szignifikáns eredmény) szintje megmutatja, hogy mekkora a valószínűsége annak, hogy a vizsgált mutatók véletlenszerűen bekövetkeznek. A jelenség általános statisztikai szignifikanciáját p-értékkel (p-szint) fejezzük ki. Bármelyik kísérletben vagy megfigyelésben valószínű, hogy a kapott adatok mintavételi hibákból származnak. Ez különösen igaz a szociológiára.
Vagyis egy statisztika statisztikailag szignifikáns, amelynek véletlenszerű előfordulásának valószínűsége rendkívül kicsi vagy szélsőséges. Ebben az összefüggésben extrémnek tekintjük a statisztika eltérésének mértékét a nullhipotézistől (egy hipotézist, amelyet ellenőrizünk a kapott mintaadatokkal való összhang szempontjából). A tudományos gyakorlatban a szignifikancia szintet az adatgyűjtés előtt választják meg, és rendszerint koefficiense 0,05 (5%). Azokban a rendszerekben, ahol a pontos értékek rendkívül fontosak, ez a mutató legfeljebb 0,01 (1%) lehet.
kórtörténet
A szignifikancia szint fogalmát Ronald Fisher, a brit statisztikus és genetikus 1925-ben vezetett be, amikor a statisztikai hipotézisek tesztelésének módszertanát dolgozta ki. Egy folyamat elemzésekor bizonyos jelenségek bizonyos valószínűséggel fennállnak. Nehézségek merülnek fel, ha kicsi (vagy nem nyilvánvaló) százalékos valószínűséggel dolgozunk, amely a "mérési hiba" fogalma alá tartozik.
Amikor az olyan statisztikákkal dolgoztak, amelyek nem elég specifikusak az ellenőrzéshez, a tudósok a nullhipotézis problémájával szembesültek, amely „zavarja” a kis mennyiségeket. Fisher javasolta az ilyen rendszerek meghatározását események valószínűsége 5% (0,05), mint kényelmes szelektív szelet, amely lehetővé teszi a nullhipotézis elutasítását a számításokban.
Rögzített együttható bevezetése
1933-ban Jerzy Neumann és Egon Pearson tudósaik munkájukban előre ajánlották (az adatgyűjtés előtt), hogy hozzanak létre egy bizonyos szintű szignifikanciát. E szabályok alkalmazásának példái jól láthatók a választások során. Tegyük fel, hogy két jelölt van, amelyek közül az egyik nagyon népszerű, a második pedig kevéssé ismert. Nyilvánvaló, hogy az első jelölt megnyeri a választást, és a második esélye általában nulla. Arra törekszenek, de nem egyenlõek: mindig fennáll a vis maior valószínûsége, szenzációs információ, váratlan döntések, amelyek megváltoztathatják a várt választási eredményeket.
Neumann és Pearson egyetértettek abban, hogy Fisher javasolt 0,05 szignifikanciaszintje (az α szimbólummal jelölve) a legmegfelelőbb. Maga Fisher azonban 1956-ban ellenezte ennek az értéknek a rögzítését. Úgy vélte, hogy az α szintjét a konkrét körülményeknek megfelelően kell meghatározni. Például a részecskefizikában ez 0,01.
Szignifikancia szintje p
A p-érték kifejezést Brownley munkájában használták először 1960-ban. A P-szint (p-érték) egy olyan mutató, amely fordítottan kapcsolódik az eredmények valódiságához. A legmagasabb p-érték a változók közötti függőség mintájának legkisebb megbízhatósági szintjének felel meg.
Ez az érték tükrözi az eredmények értelmezésével kapcsolatos hibák valószínűségét. Tegyük fel, hogy p-szint = 0,05 (1/20). Megmutatja annak az öt százaléknak a valószínűségét, hogy a mintában található változók közötti kapcsolat csak a minta véletlenszerű jellemzője.Vagyis ha ez a függőség hiányzik, akkor ismételt ilyen kísérletekkel átlagosan minden huszadik tanulmányban ugyanaz vagy nagyobb függőség várható a változók között. A p-szintet gyakran a hibaszint „elfogadható margójának” tekintik.
Egyébként a p-érték nem tükrözi a változók közötti valós összefüggést, hanem csak egy bizonyos átlagértéket mutat a feltevésekben. Különösen az adatok végleges elemzése az együttható kiválasztott értékeitől is függ. Ha p-szint = 0,05, akkor lesz néhány eredmény, mások esetén pedig 0,01-es együtthatóval.
Statisztikai hipotézisek tesztelése
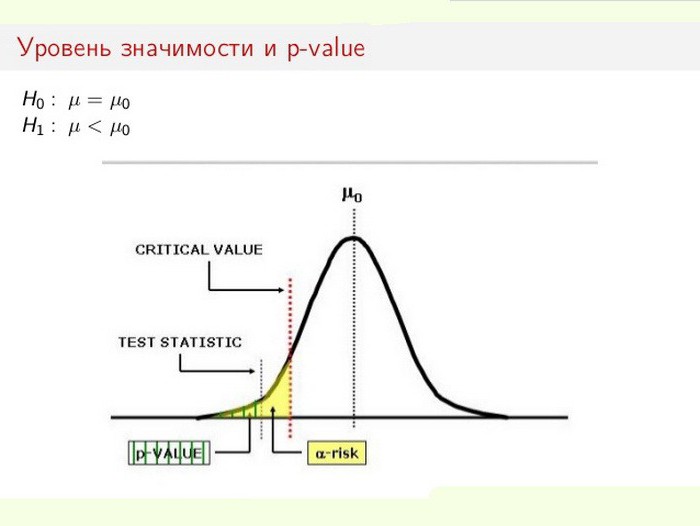
A statisztikai szignifikancia szintje különösen fontos a hipotézisek tesztelésekor. Például egy kétoldalas teszt kiszámításakor az elutasítási területet a minta eloszlása mindkét végén egyenlően osztják el (a nulla koordinátához viszonyítva), és kiszámítják az adatok valódiságát.
Tegyük fel, hogy egy bizonyos folyamat (jelenség) megfigyelésekor kiderült, hogy az új statisztikai információk a korábbi értékekhez viszonyítva kis változásokat mutatnak. Sőt, az eredmények közötti eltérések kicsik, nem nyilvánvalóak, de fontosak a tanulmány szempontjából. A dilemma a szakember előtt merül fel: a változások valóban zajlanak-e, vagy ezek a mintavételi hibák (pontatlan mérések)?
Ebben az esetben a nullhipotézist vagy használják, vagy elutasítják (mindezt hibának tulajdonítják, vagy a rendszer változását tényleges végrehajtásnak tekintik). A probléma megoldásának folyamata a teljes statisztikai szignifikancia (p-érték) és a szignifikancia szint (α) arányán alapul. Ha a p-szint <α, akkor a nullhipotézist elutasítják. Minél kisebb a p-érték, annál szignifikánsabb a tesztstatisztika.
Használt értékek
A szignifikancia szintje az elemzett anyagtól függ. A gyakorlatban a következő rögzített értékeket használják:
- a = 0,1 (vagy 10%);
- a = 0,05 (vagy 5%);
- a = 0,01 (vagy 1%);
- a = 0,001 (vagy 0,1%).
Minél pontosabbak a számítások, annál alacsonyabb az α együttható. A fizikai, kémiai, gyógyszerészeti és genetikai statisztikai előrejelzések természetesen nagyobb pontosságot igényelnek, mint a politológiában, a szociológiában.

Releváns küszöbértékek bizonyos területeken
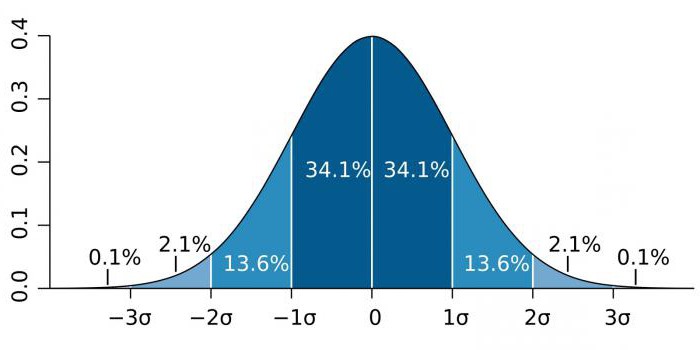
Nagy pontosságú területeken, mint például a részecskefizika és a gyártási tevékenységek, a statisztikai szignifikanciát gyakran a szórás (a szigma együtthatóval jelölt - σ) hányadosaként fejezik ki a normál valószínűség-eloszláshoz viszonyítva (Gauss-eloszlás). σ egy statisztikai mutató, amely meghatározza egy bizonyos érték értékeinek eloszlását a matematikai elvárásokhoz viszonyítva. Az események valószínűségének ábrázolására szolgál.
A tudástól függően a σ együttható nagyban változik. Például, ha előre jelezzük a Higgs-bozon létezését, akkor a σ paraméter öt (σ = 5), amely megfelel a p-értéknek = 1 / 3,5 millió értéknek. A genomok vizsgálatában a szignifikancia szint 5 × 10 lehet.-8amelyek nem ritkák ezen a területen.
hatékonyság
Ne feledje, hogy az α és p-együtthatók nem pontos jellemzők. Bármi is legyen a szignifikancia szintje a vizsgált jelenség statisztikájában, ez nem feltétlen alapja a hipotézis elfogadásának. Például, minél kisebb az α értéke, annál nagyobb az esélye, hogy a megállapított hipotézis szignifikáns. Fennáll azonban a hiba kockázata, amely csökkenti a vizsgálat statisztikai erejét (szignifikanciáját).
A kizárólag statisztikailag szignifikáns eredményekre összpontosító kutatók téves következtetéseket vonhatnak le. Ugyanakkor nehéz újra ellenőrizni a munkájukat, mivel feltételezéseket használnak (amelyek valójában α és p-értékek). Ezért mindig javasoljuk a statisztikai szignifikancia kiszámításával egy másik mutató - a statisztikai hatás nagysága - meghatározását. A hatás nagysága a hatás erősségének mennyiségi mértéke.
