מתאם וניתוח רגרסיה: דוגמה, משימות, יישום. שיטת מתאם וניתוח רגרסיה

ניתוח רגרסיה של מתאם - זו אחת השיטות הנפוצות ביותר לחקר הקשר בין ערכים מספריים. מטרתו העיקרית היא למצוא את הקשר בין שני הפרמטרים לבין דרגתם עם נגזרת המשוואה הבאה. לדוגמא, יש לנו סטודנטים שעברו את הבחינה במתמטיקה ובאנגלית. אנו יכולים להשתמש במתאם כדי לקבוע אם ההצלחה של מבחן אחד משפיעה על התוצאות בנושא אחר. לגבי ניתוח רגרסיה, זה עוזר לחזות ציונים במתמטיקה על סמך הנקודות שנקבעו בבחינה באנגלית, ולהיפך.

מהו תרשים מתאם?

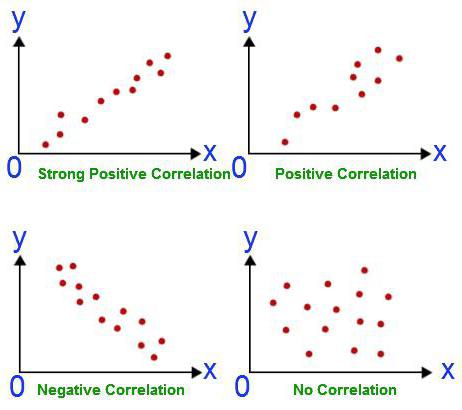
כל ניתוח מתחיל באיסוף המידע. ככל שהוא יותר כך התוצאה המתקבלת בסופו של דבר בצורה מדויקת יותר. בדוגמה לעיל, יש לנו שתי תחומים בהם התלמידים צריכים לעבור בחינה. שיעור ההצלחה שלהם הוא אומדן. ניתוח מתאם-רגרסיה מראה אם ​​התוצאה של נושא אחד משפיעה על נקודות הניקוד בבחינה השנייה. כדי לענות על שאלה זו, יש צורך לנתח במקביל את דירוגיהם של כל התלמידים. אך ראשית עליכם להחליט על המשתנה התלוי. במקרה זה, זה לא כל כך חשוב. נניח שבחינה במתמטיקה התקיימה מוקדם יותר. הנקודות עליו הן משתנה עצמאי (הן נדחות לאורך האבסיסה). אנגלית נמצאת בלוח הזמנים אחר כך. לפיכך, האומדנים המבוססים על זה הם משתנה תלוי (מתוכננים לאורך הסדר). ככל שהגרף שמתקבל כך נראה כמו קו ישר, כך המתאם הליניארי חזק יותר בין שני הערכים שנבחרו. המשמעות היא שלתלמידים במתמטיקה יש סיכוי גבוה יותר לקבל חמישיות בבחינה באנגלית.

הנחות ופשטות

שיטת המתאם וניתוח הרגרסיה כוללת מציאת קשר סיבתי. עם זאת, בשלב הראשון, עליכם להבין כי שינויים בשני הכמויות יכולים לנבוע משליש כלשהו, ​​שטרם נשקל על ידי החוקר. יתכנו גם יחסים לא לינאריים בין המשתנים, לכן קבלת מקדם השווה לאפס אינה סוף הניסוי.

מתאם ליניארי של פירסון

ניתן להשתמש במקדם זה בכפוף לשני תנאים. הראשון - כל הערכים של המשתנים הם מספרים רציונליים, השני - צפוי שהערכים ישתנו באופן יחסי. מקדם זה הוא תמיד בין -1 ל -1. אם הוא גדול מאפס, יש תלות פרופורציונאלית ישירה, פחות - הפוך, שווה - ערכים אלה אינם משפיעים זה על זה בשום דרך. היכולת לחשב אינדיקטור זה היא הבסיס לניתוח המתאם והרגרסיה. לראשונה, מקדם זה פותח על ידי קארל פירסון על בסיס רעיון פרנסיס גלטון.

נכסים וזהירות

מקדם המתאם של פירסון הוא כלי רב עוצמה, אך יש להשתמש בו בזהירות. האזהרות הבאות משמשות אותה:

1. מקדם פירסון מציין נוכחות או היעדר קשר ליניארי. ניתוח רגרסיה של מתאם אינו מסתיים בכך, יתברר כי המשתנים בכל זאת קשורים זה לזה.
2. יש להיזהר בפרשנות הערך של המקדם. ניתן למצוא מתאם בין גודל הרגליים לרמת ה- IQ.אך אין זה אומר שמדד אחד קובע אחר.
3. מקדם פירסון לא אומר דבר על הקשר הסיבתי בין המדדים.

מקדם המתאם לדרג של ספירמן

אם שינוי בערך של אינדיקטור אחד מוביל לעלייה או ירידה בערך של אחר, פירוש הדבר שהם קשורים זה לזה. ניתוח מתאם-רגרסיה, שהדוגמא שלו תינתן להלן, קשורה בדיוק לפרמטרים כאלה. מקדם דירוג מאפשר לך לפשט את החישובים.

מתאם וניתוח רגרסיה: דוגמא

נניח שקיימת הערכה ליעילותם של עשרה מפעלים. יש לנו שני שופטים שנותנים להם נקודות. לא ניתן לבצע ניתוח המתאם והרגרסיה של הארגון על בסיס מקדם פירסון הליניארי. אנו לא מעוניינים בקשר שבין דירוג השופטים. דרגות המפעלים על פי שופטים חשובות.

לניתוח מסוג זה יש היתרונות הבאים:

• צורת קשרים לא פרמטרית בין הכמויות שנחקרו.
• קלות שימוש, מכיוון שניתן לייחס את הדרגות הן בסדר עולה עולה והן בסדר יורד.

הדרישה היחידה לסוג זה של ניתוח היא הצורך להמיר את נתוני המקור.

בעיות ביישום

ניתוח המתאם והרגרסיה מבוסס על ההנחות הבאות:

• תצפיות נחשבות עצמאיות (אובדן של פי עשרה של "הנשר" אינו משפיע על התוצאה של הפוך המטבע הבא).
• בניתוח המתאם, שני המשתנים נחשבים לאקראיים. ברגרסיה - רק אחד (תלוי).
• בבדיקת השערה יש להקפיד על חלוקה תקינה. השינוי במשתנה התלוי אמור להיות זהה לכל ערך באבססיסה.
• תרשים המתאם הוא רק המבחן הראשון להשערה לגבי הקשר בין שתי סדרות הפרמטרים, ולא התוצאה הסופית של הניתוח.

תלות וסיבתיות

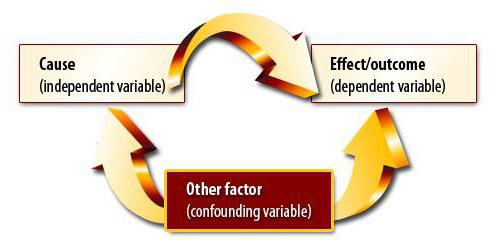
נניח שחישבנו את מקדם המתאם של נפח היצוא והתוצר. התברר שהוא שווה למודולו של האחדות. האם עשינו מתאם וניתוח רגרסיה עד הסוף? ברור שלא. התוצאה המתקבלת אינה אומרת בכלל שניתן לבטא את התוצר באמצעות ייצוא. טרם הוכחנו קשר סיבתי בין אינדיקטורים. ניתוח מתאם-רגרסיה - חיזוי ערכים של משתנה אחד בהתבסס על אחר. עם זאת, עליכם להבין שלעתים קרובות גורמים רבים משפיעים על הפרמטר. הייצוא קובע את התוצר, אך לא רק אותו. ישנם גורמים אחרים. כאן יש מתאם וקשר סיבתי, אם כי מותאם לרכיבים אחרים של התוצר המקומי הגולמי.

מצב אחר הוא הרבה יותר מסוכן. בבריטניה נערך סקר שהראה שילדים שהוריהם עישנו היו לעתים קרובות יותר עבריינים. מסקנה זו מבוססת על מתאם חזק בין המדד. אך האם הוא צודק? ראשית, התלות יכולה להיות הפוכה. הורים יכולים להתחיל לעשן בגלל לחץ בגלל העובדה שילדיהם כל הזמן נכנסים לשינויים ועוברים על החוק. שנית, שני הפרמטרים עשויים לנבוע מהשלישי. משפחות כאלה שייכות לשכבות חברתיות נמוכות, המאופיינות בשתי הבעיות. לפיכך, על סמך המתאם, לא ניתן להסיק כי קיים קשר סיבתי.

מדוע להשתמש בניתוח רגרסיה?

תלות בקורלציה כוללת מציאת קשרים בין כמויות. הקשר הסיבתי במקרה זה נותר מאחורי הקלעים. משימות המתאם וניתוח הרגרסיה חופפות רק במונחים של אישור קיומם של קשר בין ערכים של שני כמויות. עם זאת, בתחילה החוקר אינו שם לב לאפשרות לקשר סיבתי. לניתוח רגרסיה יש תמיד שני משתנים, אחד מהם תלוי. זה מתרחש במספר שלבים:

1. בחירת הדגם הנכון בשיטת הכי פחות ריבועים.
2. נגזרת משוואה המתארת ​​את ההשפעה של שינוי במשתנה עצמאי על אחר.

לדוגמה, אם אנו חוקרים את השפעת הגיל על צמיחת האדם, ניתוח רגרסיה יכול לעזור לחזות שינויים לאורך השנים.

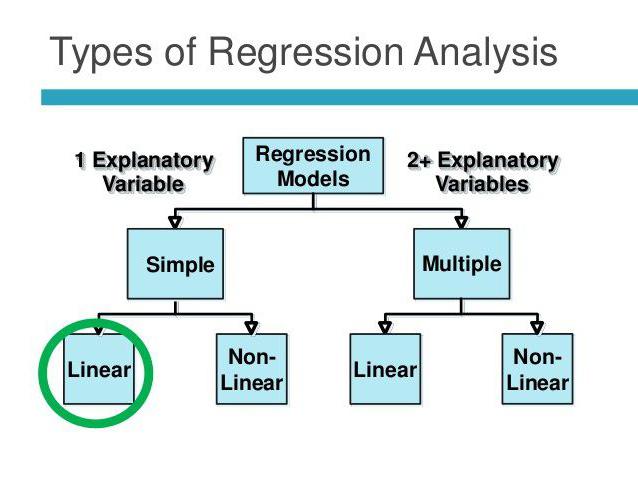
רגרסיה ליניארית ומרובה

נניח ש- X ו- Y הם שני משתנים קשורים. ניתוח רגרסיה מאפשר לנו לחזות את גודלו של אחד מהם על סמך ערכי האחר. לדוגמא, בגרות וגיל הם תסמינים תלויים. הקשר ביניהם בא לידי ביטוי באמצעות רגרסיה לינארית. למעשה, אתה יכול לבטא X דרך Y או להפך. אך לעיתים קרובות רק אחד מקווי הרגרסיה נכון. הצלחת הניתוח תלויה במידה רבה בקביעה הנכונה של המשתנה הבלתי תלוי. לדוגמא, יש לנו שני אינדיקטורים: תשואה ומשקעים. מהניסיון היומיומי מתברר שהראשון תלוי בשני ולא להפך.

רגרסיה מרובה מאפשרת לך לחשב ערך לא ידוע על בסיס ערכים של שלושה משתנים או יותר. לדוגמא, תפוקת האורז לדונם אדמה תלויה באיכות התבואה, פוריות האדמה, דשנים, טמפרטורה, וגשם. כל הפרמטרים הללו משפיעים על התוצאה הכוללת. כדי לפשט את המודל משתמשים בהנחות הבאות:

• הקשר בין מאפיינים עצמאיים להשפעה הוא לינארי.
• אי-הכללה רב-קולינרית אינה נכללת. המשמעות היא שמשתנים תלויים אינם קשורים זה לזה.
• הומוסקדסטיות ונורמליות של סדרות מספרים.

השימוש במתאם וניתוח רגרסיה

ישנם שלושה מקרים עיקריים של שימוש בשיטה זו:

1. בדיקת קשרים סתמיים בין כמויות. במקרה זה, החוקר קובע את ערכי המשתנה ומגלה אם הם משפיעים על השינוי במשתנה התלוי. לדוגמה, אתה יכול לתת לאנשים מנות שונות של אלכוהול ולמדוד את לחץ הדם שלהם. במקרה זה, החוקר יודע בוודאות כי הראשון הוא הגורם לשני, ולא להפך. ניתוח רגרסיה של מתאם מאפשר לזהות קשר לינארי פרופורציונאלי ישיר בין שני המשתנים הללו ולהפיק נוסחה המתארת ​​זאת. במקרה זה, ניתן להשוות ערכים המובעים ביחידות מדידה שונות לחלוטין.
2. מציאת קשר בין שני משתנים מבלי להרחיב קשר סיבתי אליהם. במקרה זה, אין הבדל באיזה גודל החוקר מכנה תלוי. יתרה מזאת, במציאות יתכן כי שניהם מושפעים מהמשתנה השלישי, ולכן הם משתנים באופן יחסי.
3. חישוב הערכים של כמות אחת בהתבסס על כמות אחרת. זה מבוסס על משוואה בה מחליפים מספרים ידועים.

לפיכך, ניתוח מתאם כרוך במציאת קשר (לא סיבתי) בין משתנים, וניתוח רגרסיה מסביר זאת, לרוב תוך שימוש בפונקציה מתמטית.