במודל סטטיסטי, ניתוח רגרסיה הוא מחקר המשמש להערכת הקשר בין משתנים. שיטה מתמטית זו כוללת שיטות רבות נוספות לעיצוב וניתוח של מספר משתנים, כאשר המיקוד הוא על הקשר בין המשתנה התלוי לאחד או יותר עצמאי. ליתר דיוק, ניתוח רגרסיה מסייע להבין כיצד ערך אופייני של משתנה תלוי משתנה אם אחד המשתנים הבלתי תלויים משתנה, ואילו המשתנים האחרים הבלתי תלויים נשארים קבועים.

בכל המקרים הערכת היעד היא פונקציה של משתנים עצמאיים והיא נקראת פונקציית הרגרסיה. בניתוח הרגרסיה, מעניין גם לאפיין את השינוי במשתנה התלוי כפונקציה של רגרסיה, אותה ניתן לתאר באמצעות חלוקת הסתברות.
משימות ניתוח רגרסיה
שיטת מחקר סטטיסטית זו נמצאת בשימוש נרחב לחיזוי, כאשר לשימוש שלה יש יתרון משמעותי, אך לעיתים היא יכולה להוביל לאשליות או קשרים כוזבים, ולכן מומלץ להשתמש בזה בזהירות בנושא זה, מכיוון שלתאם, למשל, אין פירושו קשר סיבתי.
פותחו מספר רב של שיטות לביצוע ניתוח רגרסיה, כמו רגרסיה לינארית ופחות ריבועית, שהם פרמטריים. המהות שלהם היא שפונקציית הרגרסיה מוגדרת במונחים של מספר סופי של פרמטרים לא ידועים המוערכים מהנתונים. רגרסיה לא-פרמטרית מאפשרת לפונקציות שלה לשכב במערכת פונקציות מסוימת, שיכולה להיות ממדית אינסופית.
כשיטת מחקר סטטיסטית, ניתוח הרגרסיה הלכה למעשה תלוי בצורה של תהליך ייצור הנתונים וכיצד הוא מתקשר לגישת הרגרסיה. מכיוון שהצורה האמיתית של תהליך הנתונים מייצרת ככלל מספר לא ידוע, ניתוח הרגרסיה של הנתונים לעיתים קרובות תלוי במידה מסוימת בהנחות לגבי תהליך זה. לפעמים ההנחות מאומתות אם יש מספיק נתונים זמינים. מודלים של רגרסיה מועילים לעתים קרובות גם כאשר ההנחות מופרות בינוני, אם כי אינן יכולות לעבוד ביעילות מירבית.
במובן הצר יותר, רגרסיה עשויה להתייחס באופן ספציפי להערכה של משתני תגובה רציפים, בניגוד למשתני התגובה הנפרדים ששימשו בסיווג. המקרה של משתנה פלט רציף נקרא גם רגרסיה מטרית על מנת להבדיל אותו מבעיות קשורות.
הסיפור
צורת הרגרסיה המוקדמת ביותר היא שיטת הידועים פחות בריבועים. היא פורסמה על ידי Legendre בשנת 1805 וגאוס בשנת 1809. Legendre and Gauss החלו את השיטה למשימה לקבוע מתוך תצפיות אסטרונומיות מסלולי גופות סביב השמש (בעיקר שביטים, אך לימים כוכבי לכת חדשים שהתגלו לאחרונה). גאוס פרסם פיתוח נוסף של תיאוריית הריבועים הפחות טובים בשנת 1821, כולל גרסה של משפט גאוס-מרקוב.

את המונח "רגרסיה" טבע פרנסיס גלטון במאה ה -19 כדי לתאר תופעה ביולוגית. בשורה התחתונה, גידול צאצאים מגידול אבות, ככלל, נסוג לממוצע הרגיל.מבחינת גלטון, לרגרסיה הייתה רק משמעות ביולוגית זו, אך בהמשך עבודתו המשיכו על ידי אודני יול וקארל פירסון והובאו להקשר סטטיסטי כללי יותר. בעבודתם של יול ופירסון, ההתפלגות המשותפת של משתני התגובה ומשתני ההסבר נחשבת לגאוסית. הנחה זו נדחתה על ידי פישר ביצירות 1922 ו- 1925. פישר הציע שההפצה המותנית של משתנה התגובה היא גאוסית, אך חלוקת המפרקים לא צריכה להיות. בעניין זה, הנחתו של פישר קרובה יותר לניסוח גאוס משנת 1821. עד 1970 לקח לפעמים עד 24 שעות להגיע לתוצאה של ניתוח רגרסיה.

שיטות ניתוח רגרסיה ממשיכות להיות תחום של מחקר פעיל. בעשורים האחרונים פותחו שיטות חדשות לרגרסיה אמינה; רגרסיה הכוללת תגובות מתואמות; שיטות רגרסיה המאכלסות סוגים שונים של נתונים חסרים; רגרסיה לא-פרמטרית; שיטות רגרסיה בייסיות; רגרסיות בהן נמדדים משתני חיזוי בשגיאה; רגרסיות עם יותר מנבאים מאשר תצפיות, כמו גם מסקנות סיבתיות עם רגרסיה.
מודלים של רגרסיה
מודלים של ניתוח רגרסיה כוללים את המשתנים הבאים:
- פרמטרים לא ידועים, המיועדים לבטא, שעשויים להיות סולם או וקטור.
- משתנים עצמאיים, X.
- משתנים תלויים, י.
בתחומים שונים של מדע בהם מיושם ניתוח רגרסיה, משתמשים במונחים שונים במקום משתנים תלויים ועצמאיים, אך בכל המקרים מודל הרגרסיה מתייחס ל- Y לפונקציות X ו- β.
הקירוב בדרך כלל צורה E (Y | X) = F (X, β). כדי לבצע ניתוח רגרסיה, יש לקבוע את סוג הפונקציה f. פחות נפוץ, זה מבוסס על ידע על הקשר בין Y ל- X שאינם מסתמכים על נתונים. אם ידע כזה אינו זמין, נבחר טופס F גמיש או נוח.
משתנה תלוי Y
כעת נניח שלווקטור של הפרמטרים הלא ידועים β יש אורך k. כדי לבצע ניתוח רגרסיה, המשתמש צריך לספק מידע אודות המשתנה התלוי Y:
- אם יש נקודות נתונים של N בצורה (Y, X), בהן N
- אם נצפים N = K בדיוק, והפונקציה F היא לינארית, אז ניתן לפתור את המשוואה Y = F (X, β) בדיוק ולא בערך. זה מפחית לפיתרון קבוצה של משוואות N עם אלמונים N (אלמנטים של β), שיש לה פיתרון ייחודי כל עוד X אינו תלוי באופן לינארי. אם F אינו לינארי, ייתכן שהפתרון אינו קיים, או פתרונות רבים עשויים להתקיים.
- הנפוץ ביותר הוא המצב בו נצפות N> נקודות על הנתונים. במקרה זה, יש מספיק נתונים בנתונים כדי להעריך את הערך הייחודי עבור β המתאים ביותר לנתונים, ומודל הרגרסיה, כאשר הוא מוחל על הנתונים יכול להיחשב כמערכת מוגדרת יתר ב- β.
במקרה האחרון, ניתוח רגרסיה מספק כלים ל:
- מציאת פתרונות לפרמטרים לא ידועים β, אשר, למשל, יצמצמו את המרחק בין הערכים שנמדדו והניבוי של Y.
- תחת הנחות סטטיסטיות מסוימות, ניתוח רגרסיה משתמש במידע עודף כדי לספק מידע סטטיסטי על פרמטרים לא ידועים β והערכים החזויים של המשתנה התלוי Y.
מספר הכרחי של מדידות עצמאיות
שקול מודל רגרסיה שיש בו שלושה פרמטרים לא ידועים: β0, β1 ו- β2. נניח שהנסיין מבצע 10 מדידות באותו ערך של המשתנה הבלתי תלוי של הווקטור X.במקרה זה, ניתוח הרגרסיה אינו מספק מערך ערכים ייחודי. הדבר הטוב ביותר שתוכלו לעשות הוא להעריך את הממוצע וסטיית התקן של המשתנה התלוי Y. על ידי מדידת שני ערכי X שונים באותו אופן, תוכלו לקבל נתונים מספיקים לרגרסיה עם שני אלמונים, אך לא לשלושה אלמונים או יותר.

אם מדידות הנסיין בוצעו בשלושה ערכים שונים של המשתנה הבלתי תלוי של הווקטור X, ניתוח הרגרסיה יספק מערך ייחודי של הערכות לשלושה פרמטרים לא ידועים ב- β.
במקרה של רגרסיה לינארית כללית, האמירה לעיל שווה לדרישה כי המטריצה XטX הפיך.
הנחות סטטיסטיות
כאשר מספר המדידות N גדול ממספר הפרמטרים הלא ידועים k ושגיאת המדידה εiלאחר מכן, ככלל, עודף המידע הכלול במדידות מופץ ומשמש לתחזיות סטטיסטיות לגבי פרמטרים לא ידועים. עודף המידע הזה נקרא מידת חופש הרגרסיה.
הנחות יסוד
הנחות קלאסיות לניתוח רגרסיה כוללות:
- המדגם מייצג את תחזית ההשלכות.
- השגיאה היא משתנה אקראי עם ערך ממוצע של אפס, המותנה במשתני ההסבר.
- משתנים עצמאיים נמדדים ללא שגיאה.
- כמשתנים עצמאיים (מנבאים), הם אינם תלויים באופן ליניארי, כלומר לא ניתן לבטא שום חיזוי בצורה של שילוב לינארי של האחרים.
- שגיאות אינן מתואמות, כלומר מטריצת המזוריות של טעויות אלכסוניות וכל אלמנט שאינו נפרד הם שונות של השגיאה.
- שונות השגיאה קבועה על פי התצפיות (הומוסקדסטיות). אם לא, תוכלו להשתמש בשיטת המשבצות הכי פחות משוקללות או בשיטות אחרות.
תנאים מספקים אלה לאומדן הריבועים הנמוכים ביותר הם בעלי המאפיינים הנדרשים, בפרט, הנחות אלה גורמות כי אומדני הפרמטרים יהיו אובייקטיביים, עקביים ויעילים, במיוחד כאשר נלקחים בחשבון בכיתה של הערכות ליניאריות. חשוב לציין כי עדויות לעיתים רחוקות עומדות בתנאים. כלומר, השיטה משמשת גם אם ההנחות אינן נכונות. וריאציה של הנחות יכולה לפעמים לשמש כמדד עד כמה מועיל מודל זה. ניתן להקל על הרבה מהנחות אלה בשיטות מתקדמות יותר. דוחות ניתוח סטטיסטי כוללים בדרך כלל ניתוח בדיקות המבוססות על נתוני מדגם ומתודולוגיה לתועלת המודל.
בנוסף, משתנים במקרים מסוימים מתייחסים לערכים הנמדדים במיקומי נקודה. יתכנו מגמות מרחביות והתאמה אוטומטית מרחבית במשתנים המפרים את ההנחות הסטטיסטיות. רגרסיה משוקללת גיאוגרפית היא השיטה היחידה העוסקת בנתונים כאלה.
ניתוח רגרסיה לינארית
ברגרסיה לינארית תכונה היא שהמשתנה התלוי, שהוא Yiהוא שילוב פרמטרי ליניארי. לדוגמה, ברגרסיה לינארית פשוטה, משתנה אחד עצמאי, x, משמש למודל נקודות ni, ושני פרמטרים, β0 ו- β1.
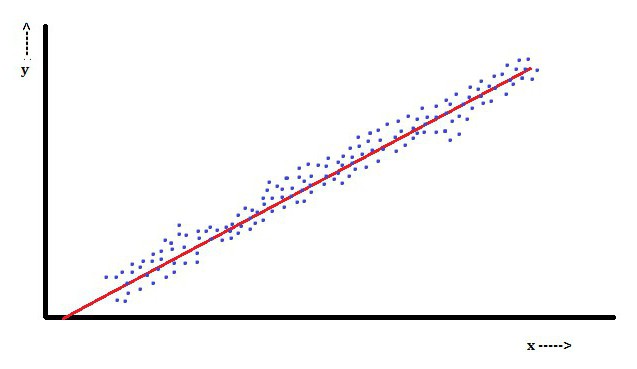
עם רגרסיה לינארית מרובה, ישנם מספר משתנים עצמאיים או הפונקציות שלהם.
בעזרת דגימה אקראית מאוכלוסייה, הפרמטרים שלה מאפשרים לקבל דוגמא למודל רגרסיה לינארית.
בהיבט זה, שיטת הפחות ריבועים היא הפופולרית ביותר. באמצעותו מתקבלים הערכות פרמטרים שממזערים את סכום שאריות הריבוע. מינימום מסוג זה (המאפיין רגרסיה לינארית) של פונקציה זו מוביל לקבוצת משוואות נורמליות ולקבוצה של משוואות לינאריות עם פרמטרים שנפתרים לקבלת הערכות פרמטרים.
תחת ההנחה הנוספת כי בדרך כלל שגיאת אוכלוסיה מתפשטת, החוקר יכול להשתמש באומדני שגיאה סטנדרטיים אלה כדי ליצור מרווחי ביטחון ולבחון השערות לגבי הפרמטרים שלה.
ניתוח רגרסיה לא לינארי
דוגמא בה הפונקציה אינה לינארית ביחס לפרמטרים מצביעה על כך שצריך למזער את סכום המשבצות באמצעות נוהל איטרטיבי. זה מציג סיבוכים רבים שקובעים את ההבדלים בין שיטות ריבועיות פחות לינאריות ובלתי לינאריות. כתוצאה מכך, תוצאות ניתוח הרגרסיה בשיטה הלא לינארית לעיתים אינן ניתנות לחיזוי.
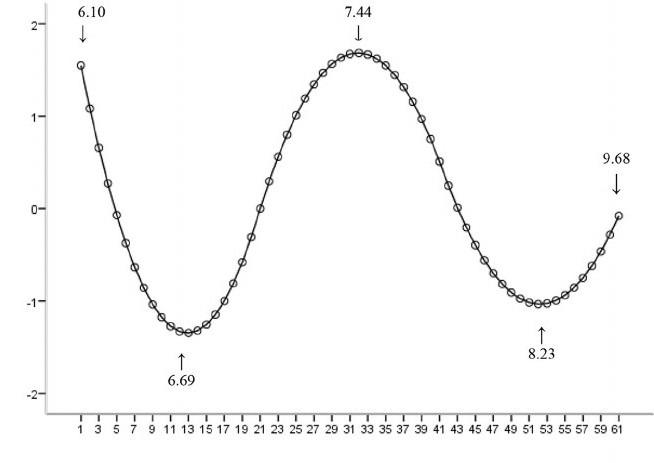
חישוב הכוח וגודל המדגם
כאן, ככלל, אין שיטות עקביות ביחס למספר התצפיות בהשוואה למספר המשתנים הבלתי תלויים במודל. הכלל הראשון הוצע על ידי גוד והרדין ונראה כמו N = t ^ n, כאשר N הוא גודל המדגם, n הוא מספר המשתנים העצמאיים, ו- t הוא מספר התצפיות הנחוצות כדי להשיג את הדיוק הרצוי אם לדגם היה רק משתנה עצמאי אחד. לדוגמה, חוקר בונה מודל רגרסיה לינארי באמצעות מערך נתונים המכיל 1000 חולים (N). אם החוקר מחליט שצריך חמש תצפיות כדי לקבוע במדויק את הקו (m), המספר המרבי של המשתנים הבלתי תלויים שהמודל יכול לתמוך הוא 4.
שיטות אחרות
למרות העובדה כי הפרמטרים של מודל הרגרסיה בדרך כלל מוערכים בשיטת הכי פחות ריבועים, ישנן שיטות אחרות שמשתמשות בהן בתדירות נמוכה הרבה יותר. לדוגמה, אלה הן השיטות הבאות:
- שיטות בייסיות (למשל שיטת רגרסיה ליניארית בייסית).
- רגרסיה באחוזים, המשמשת במצבים בהם הפחתה באחוז טעויות נחשבת מתאימה יותר.
- הסטיות המוחלטות הקטנות ביותר, שהן יציבות יותר בנוכחות מחיצות המובילות לרגרסיה קוונטית.
- רגרסיה לא-פרמטרית, הדורשת מספר רב של תצפיות וחישובים.
- מרחק מדד הלמידה הנלמד בחיפוש אחר מרחק מטרי משמעותי במרחב קלט נתון.
תוכנה
כל חבילות התוכנה הסטטיסטיות העיקריות מבוצעות באמצעות ניתוח רגרסיה לפחות ריבועים. ניתן להשתמש ברגרסיה לינארית פשוטה וניתוח רגרסיה מרובה בכמה יישומים של הגיליון האלקטרוני, כמו גם במחשבים מסוימים. למרות שחבילות תוכנה סטטיסטיות רבות יכולות לבצע רגרסיה לא-פרמטרית ואמינה מסוגים שונים, שיטות אלה פחות סטנדרטיות; חבילות תוכנה שונות מיישמות שיטות שונות. תוכנת רגרסיה מתמחה פותחה לשימוש בתחומים כמו ניתוח בדיקות והדמיית עצבים.






