ניתוח רב משתנה של שונות

ניתוח השונות הוא קבוצה של שיטות סטטיסטיות שנועדו לבחון השערות לגבי הקשר בין סימנים מסוימים לגורמים הנחקרים, שאין להם תיאור כמותי, כמו גם לקבוע את מידת ההשפעה של גורמים ואת האינטראקציה שלהם. בספרות המקצועית זה נקרא לעתים קרובות ANOVA (מהשם האנגלי Analyse of Variations). שיטה זו פותחה לראשונה על ידי ר 'פישר בשנת 1925.

סוגים וקריטריונים של ניתוח השונות

שיטה זו משמשת לחקר הקשר בין תכונות איכותיות (נומינליות) ומשתנה כמותי (רציף). למעשה, הוא בוחן את ההשערה כי הממוצע האריתמטי של מספר דגימות שווה. לפיכך, זה יכול להיחשב כקריטריון פרמטרי להשוואה בין מרכזי מספר דוגמאות בבת אחת. אם אתה משתמש בשיטה זו לשתי דוגמאות, תוצאות ניתוח השונות יהיו זהות לתוצאות מבחן t-student. עם זאת, בניגוד לקריטריונים אחרים, מחקר זה מאפשר לנו ללמוד את הבעיה ביתר פירוט.

ניתוח השונות בסטטיסטיקה מבוסס על החוק: סכום הריבועים של סטיות המדגם המשולב שווה לסכום המשבצות של הסטיות בין הקבוצות לבין סכום המשבצות של הסטיות הבינאומיות. לצורך המחקר, מבחן פישר משמש לבחינת המשמעות של ההבדל בין שונות בין קבוצות לשונות בין קבוצות. עם זאת, לשם כך, התנאים המוקדמים הנדרשים הם ההתפלגות התקינה וההומוסקקטסטיות (שוויון שונות) של הדגימות. הבחינו בין ניתוח שונות של חד ממדי (חד-משתנה) לבין רב משתנים (רב משתנים). הראשון שוקל את התלות של הכמות הנחקרת במאפיין אחד, השני - מייד על רבים, וגם מאפשר לך לזהות את הקשר ביניהם.

גורמים

גורמים נקראים נסיבות מבוקרות המשפיעות על התוצאה הסופית. רמתו או שיטת העיבוד שלו נקראת הערך המאפיין את הביטוי הספציפי של מצב זה. מספרים אלה ניתנים בדרך כלל בסולם נומינלי או סדרתי. לעיתים קרובות, ערכי הפלט נמדדים במאזניים כמותיים או קבועים. ואז עולה הבעיה של קיבוץ נתוני הפלט בסדרת תצפיות, התואמות בערך אותם ערכים מספריים. אם כמות הקבוצות נראית גדולה מדי, ייתכן שמספר התצפיות בהן אינו מספיק בכדי להשיג תוצאות אמינות. אם אתה לוקח את המספר קטן מדי, זה יכול להוביל לאובדן של תכונות משמעותיות של ההשפעה על המערכת. האופן שבו הסיווג של נתונים מקובץ תלוי בנפח ואופי השונות בערכים. מספר וגודל המרווחים בניתוח חד כיווני נקבע לרוב על ידי עקרון המרווחים השווים או על ידי עקרון התדרים שווים.

ניתוח בעיות שונות

אז, ישנם מקרים בהם עליכם להשוות בין שתי דוגמאות או יותר. לאחר מכן רצוי להשתמש בניתוח שונות. שם השיטה מצביע על כך שמסקנות מסקנות ממחקר מרכיבי השונות. מהות המחקר היא שהשינוי הכללי במדד מחולק לחלקים רכיבים התואמים את פעולתו של כל גורם בודד. שקול מספר בעיות שניתוח טיפוסי של שונות פותר.

דוגמא 1

בסדנה מספר כלי מכונה - מכונות אוטומטיות המייצרות חלק מסוים. הגודל של כל חלק הוא ערך אקראי, התלוי בהגדרות של כל מכונה ובסטיות אקראיות המתרחשות במהלך ייצור החלקים.יש לקבוע אם המכונות מוגדרות באותה מידה לפי מדידות מידות החלקים.

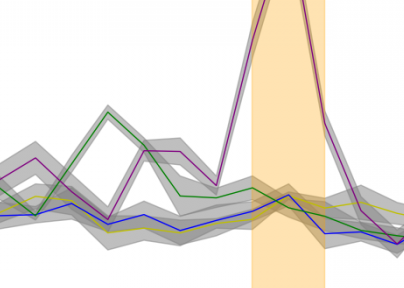
דוגמא 2

במהלך ייצור המנגנון החשמלי משתמשים בסוגים שונים של נייר בידוד: הקבל, החשמל וכו '. ניתן לספוג את המנגנון בחומרים שונים: שרף אפוקסי, לכה, שרף ML-2 וכו'. ניתן לחסל דליפות תחת ואקום בלחץ גבוה, על ידי חימום. זה יכול להיות ספוג על ידי טבילה בלכה, תחת זרם לכה רציף וכו '. המנגנון החשמלי בכללותו מוזג עם תרכובת מסוימת, אשר קיימות מספר אפשרויות. אינדיקטורים איכותיים הם החוזק הדיאלקטרי של הבידוד, טמפרטורת התחממות יתר של הפיתול במצב הפעלה, ומספר אחרים. במהלך בדיקת התהליך הטכנולוגי של מנגנוני ייצור, יש לקבוע כיצד כל אחד מהגורמים הרשומים משפיע על ביצועי המנגנון.

דוגמא 3

מחסן הטרוליבוס משרת מספר נתיבי טרוליבוס. סוגים שונים של טרוליבוסים עובדים עבורם ואיסוף דמי נסיעה נאסף על ידי 125 בקרים. הנהלת המחסן מתעניינת בשאלה: כיצד ניתן להשוות בין הביצועים הכלכליים של כל בקר (הכנסות) תוך התחשבות בנתיבים שונים, סוגים שונים של אוטובוסים לטרולי? כיצד לקבוע את הכדאיות הכלכלית בשחרור סוג מסוים של טרוליבוס במסלול מסוים? כיצד לקבוע דרישות סבירות לכמות ההכנסות שהמוליך מביא בכל מסלול בסוגים שונים של אוטובוסים עגלה?

המשימה של בחירת שיטה היא כיצד לקבל את המידע המרבי לגבי ההשפעה על התוצאה הסופית של כל גורם, לקבוע את המאפיינים המספריים של השפעה כזו, את אמינותם בעלות הנמוכה ביותר ובזמן הקצר ביותר. לפתור בעיות כאלה אפשר שיטות ניתוח שונות.

ניתוח חד כיווני

המחקר נועד להעריך את גודל ההשפעה של מקרה מסוים על הסקירה שניתחה. משימה נוספת של ניתוח חד כיווני עשויה להיות להשוות בין שתי נסיבות או יותר אחת לשנייה על מנת לקבוע את ההבדל בהשפעתן על ההיזכרות. אם ההשערה האפסית נדחית, השלב הבא יהיה הערכה כמותית ובניית מרווחי ביטחון עבור המאפיינים המתקבלים. במקרה כאשר השערת אפס אי אפשר להשליך, בדרך כלל זה מתקבל ומסקנה לגבי מהות ההשפעה.

ניתוח שונות של שונות יכול להפוך לאנלוג לא-פרמטרי לשיטת הדירוג קרסקל-וואליס. זה פותח על ידי המתמטיקאי האמריקני וויליאם קרסקל והכלכלן וילסון וואליס בשנת 1952. קריטריון זה הוטל על מנת לבחון את השערת האפס כי ההשפעות על הדגימות שנחקרו שוות לערכים ממוצעים לא ידועים אך שווים. מספר הדגימות צריך להיות יותר משניים.

הקריטריון של Jonkhier (Jonkhier-Terpstra) הוצע באופן עצמאי על ידי המתמטיקאי ההולנדי T.J. Terpstrom בשנת 1952 והפסיכולוג הבריטי E.R. Jonkhier בשנת 1954. הוא משמש כאשר ידוע מראש שקבוצות התוצאות הזמינות מסודרות על ידי גידול ההשפעה של הגורם הנחקר, הנמדד בסולם רגיל.

M - מבחן ברטלט, שהוצע על ידי הסטטיסטיקאי הבריטי מוריס סטיבנסון ברטלט בשנת 1937, משמש לבדיקת השערת האפס לגבי שוויון השונות בין כמה אוכלוסיות כלליות נורמליות מהן נלקחו הדגימות שנחקרו, ובדרך כלל בעלות נפחים שונים (מספר כל מדגם צריך להיות לפחות ארבע )

G הוא מבחן ה- Cochren, שהתגלה על ידי ויליאם גממל Cochren האמריקאי בשנת 1941. הוא משמש לבדיקת השערת האפס כי השונות של אוכלוסיות כלליות נורמליות שוות עבור דגימות עצמאיות של נפח שווה.

הקריטריון של לבנה הלא-פרמטרי, שהוצע על ידי המתמטיקאי האמריקני האוורד לוין בשנת 1960, הוא אלטרנטיבה לקריטריון של ברטלט בתנאים בהם אין כל וודאות כי הדגימות הנחקרות מצייתות להתפלגות התקינה.

בשנת 1974 הציעו סטטיסטיקאים אמריקאים מורטון ב 'בראון ואלן ב' פורסייט מבחן (קריטריון בראון-פורסיטה), השונה במקצת מקריטריון לובן.

ניתוח דו-גורמי

ניתוח דו כיווני של שונות משמש לדגימות משולבות בדרך כלל. בפועל משתמשים לרוב בטבלאות מורכבות בשיטה זו, בפרט אלו בהן כל תא מכיל מערכת נתונים (מדידות חוזרות) המתאימות לערכי רמה קבועים. אם לא מתקיימות ההנחות הדרושות ליישום ניתוח דו-כיווני של שונות, נעשה שימוש בקריטריון הדרגה הלא-פרמטרי (פרידמן, קנדל וסמית ') שפותח על ידי הכלכלן האמריקני מילטון פרידמן בסוף 1930. קריטריון זה אינו תלוי בסוג ההתפלגות.

ההנחה היא כי חלוקת הכמויות זהה ורציפה והם אינם תלויים זה בזה. בבדיקת השערת האפס מוצגת הפלט בצורה של מטריצה ​​מלבנית בה השורות מתאימות לרמות של גורם B והעמודות תואמות לרמות של A. כל תא בטבלה (בלוק) יכול להיות תוצאה של מדידות של פרמטרים על אובייקט אחד או על קבוצת עצמים בערכים קבועים של הרמות של שני הגורמים. . במקרה זה, הנתונים המתאימים מסופקים כערכים הממוצעים של פרמטר מסוים עבור כל המדידות או האובייקטים של המדגם הנחקר. כדי להחיל את הקריטריון של נתוני הפלט, יש צורך לעבור מתוצאות המדידה הישירות לדרגתן. הדירוג מתבצע עבור כל שורה בנפרד, כלומר הערכים מסודרים לכל ערך קבוע.

קריטריון עמוד (קריטריון L), שהוצע על ידי הסטטיסטיקאי האמריקני E. B. Page בשנת 1963, נועד לבחון את השערת האפס. עבור דגימות גדולות משתמשים בקירוב העמודים. הם, בכפוף למציאות של השערות האפס המתאימות, מצייתים להתפלגות התקינה הרגילה. במקרה שלשורות בטבלת המקורות אותם ערכים, יש צורך להשתמש בדרגות ממוצעות. יתר על כן, הדיוק של המסקנות יהיה גרוע יותר, כך יהיו מספרים של צירופי מקרים כאלה.

Q הוא הקריטריון של Cochren שהוצע על ידי V. Cohren בשנת 1937. הוא משמש במקרים בהם קבוצות של נבדקים הומוגניים נחשפים ליותר משניים ועבורם שתי תגובות אפשריות - שליליות על תנאי (0) וחיוביות על תנאי (1) . השערת האפס מורכבת מהשפעות שוות של השפעה. ניתוח דו-כיווני של שונות מאפשר לקבוע את קיומם של אפקטים מעובדים, אך אינו מאפשר לקבוע עבור אילו עמודות אפקט זה קיים. כדי לפתור בעיה זו משתמשים בשיטה של ​​מספר משוואות Sheff לדגימות מצומדות.

ניתוח רב משתנים

המשימה של ניתוח רב משתנים של שונות מתעוררת כאשר יש צורך לקבוע את השפעתם של שני תנאים או יותר על משתנה אקראי מסוים. המחקר מספק נוכחות של משתנה אקראי אחד תלוי, הנמדד בסולם ההבדל או היחסים, וכמה משתנים עצמאיים, שכל אחד מהם בא לידי ביטוי בסולם השמות או בדרגה. ניתוח נתוני השונות הוא קטע מפותח למדי בסטטיסטיקה מתמטית, שיש בו הרבה אפשרויות. תפיסת המחקר נפוצה הן עבור גורם יחיד והן עבור ריבוי גורמים. מהותה היא שהשונות הכוללת מחולקת לרכיבים, התואמים לקבוצת נתונים מסוימת. לכל קיבוץ נתונים יש מודל משלה.כאן נשקול רק את ההוראות הבסיסיות הדרושות להבנה ושימוש מעשי באפשרויות הנפוצות ביותר שלה.

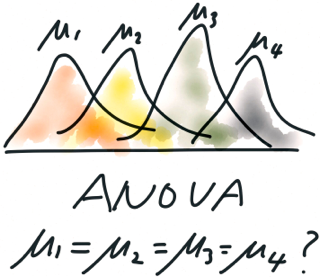
ניתוח שונות של גורמים דורש יחס זהיר למדי לאיסוף והצגת נתוני קלט ובעיקר לפרשנות התוצאות. בשונה מגורם אחד, שאת תוצאותיו ניתן למקם באופן שרירותי ברצף מסוים, תוצאות הדו-גורמים דורשות ייצוג מורכב יותר. מצב קשה עוד יותר מתעורר כאשר ישנן שלוש, ארבע או יותר נסיבות. בגלל זה, יותר משלושה (ארבעה) תנאים נכללים לעתים נדירות במודל. דוגמא לכך היא התרחשות התהודה בערך מסוים של הקיבול והשראות של המעגל החשמלי; ביטוי של תגובה כימית עם קבוצה מסוימת של אלמנטים מהם המערכת בנויה; התרחשות של השפעות חריגות במערכות מורכבות עם צירוף מקרים מסוים של נסיבות. נוכחות של אינטראקציה יכולה לשנות באופן מהותי את מודל המערכת ולעיתים להביא לחשיבה מחודשת על אופי התופעות עמן הנסיין מתמודד.

ניתוח רב משתנים של שונות עם ניסויים חוזרים

לעתים קרובות ניתן לקבץ נתוני מדידה לא על ידי שניים, אלא על ידי מספר גדול יותר של גורמים. לכן, אם ניקח בחשבון את ניתוח השונות של אורך חיי השירות של צמיגי גלגלי האוטובוסים של העגלה תוך התחשבות בנסיבות (היצרן והמסלול בו פועלים הצמיגים), נוכל להבחין בעונה שבה מפעילים את הצמיגים (כלומר, פעולת החורף והקיץ) כתנאי נפרד. כתוצאה מכך תהיה לנו המשימה של שיטת שלושה גורמים.

אם ישנם יותר תנאים, הגישה זהה לניתוח הדו-גורמים. בכל המקרים, הם מנסים לפשט את הדגם. תופעת האינטראקציה בין שני גורמים לא באה לידי ביטוי לעתים קרובות כל כך, ואינטראקציה משולשת מתרחשת רק במקרים חריגים. הם כוללים את האינטראקציה שלגביהם יש מידע קודם וסיבות טובות לקחת זאת בחשבון במודל. תהליך בידוד הגורמים האישיים והתחשבות בהם הוא פשוט יחסית. לכן, לעיתים קרובות יש רצון להדגיש יותר נסיבות. זה לא צריך להיסחף. ככל שתנאים רבים יותר, כך הדגם הופך להיות פחות אמין וגדלה ההסתברות לטעות. המודל עצמו, הכולל מספר רב של משתנים עצמאיים, הופך להיות קשה די לפרשנות ולא נוח לשימוש מעשי.

הרעיון הכללי של ניתוח השונות

ניתוח השונות בסטטיסטיקה הוא שיטה להשגת תוצאות תצפיות התלויות בנסיבות קיימות במקביל, ולהעריך את השפעתן. משתנה מבוקר שתואם את שיטת ההשפעה על מושא הלימוד ובפרק זמן מסוים רוכש ערך מסוים נקרא גורם. הם יכולים להיות איכותיים וכמותיים. רמות של תנאים כמותיים רוכשות ערך מסוים בסדר גודל מספרי. דוגמאות לכך הן טמפרטורה, לחץ, כמות חומר. גורמים איכותיים הם חומרים שונים, שיטות טכנולוגיות שונות, מכשירים, חומרי מילוי. הרמות שלהם תואמות את סולם השמות.

האיכות יכולה לכלול גם את סוג חומר האריזה, תנאי האחסון של צורת המינון. זה גם רציונלי לייחס את מידת הטחינה של חומרי גלם, את ההרכב השברירי של גרגירים שהם בעלי חשיבות כמותית, אך קשה לשלוט אם משתמשים בסולם כמותי. מספר גורמי האיכות תלוי בסוג צורת המינון, כמו גם בתכונות הפיזיות והטכנולוגיות של חומרי הרפואה. לדוגמא ניתן להשיג טבליות מחומרים גבישיים על ידי דחיסה ישירה. במקרה זה, די בבחירת חומרי הזזה ושמן.

דוגמאות לגורמים איכותיים לסוגים שונים של צורות מינון

• טינקטורות. הרכב המיצוי, סוג החילוץ, שיטת הכנת חומרי הגלם, שיטת הייצור, שיטת הסינון.
• תמציות (נוזלי, סמיך, יבש). הרכב המיצוי, שיטת המיצוי, סוג ההתקנה, שיטת הסרת החילוץ וחומרים נטל.
• גלולות הרכב תוספים, חומרי מילוי, פירוק, קלסרים, חומרי סיכה ודביקות. שיטה לייצור טבליות, סוג ציוד עיבוד. סוג הקליפה ומרכיביה, יוצרי סרטים, פיגמנטים, צבעים, פלסטייזרים, ממסים.
• פתרונות הזרקה. סוג הממס, שיטת סינון, אופי מייצבים וחומרים משמרים, תנאי עיקור, שיטת מילוי אמפולות.
• כלי גידול. הרכב בסיס המשקעים, שיטה לייצור משקעים, חומרי מילוי, אריזה.
• משחות. הרכב הבסיס, רכיבים מבניים, שיטת הכנת המשחה, סוג הציוד, האריזה.
• כמוסות סוג חומר הקליפה, שיטת ייצור כמוסות, סוג של פלסטייזר, חומר משמר, צבע.
• לינימנט. שיטת ההכנה, ההרכב, סוג הציוד, סוג התחליב.
• השעיות סוג הממס, סוג המייצב, שיטת הפיזור.

דוגמאות לגורמים איכותיים ורמותיהם שנלמדו בתהליך הייצור של טבליות

• אבקת אפייה. עמילן תפוח אדמה, חימר לבן, תערובת של נתרן ביקרבונט עם חומצת לימון, מגנזיום פחמתי בסיסי.
• פתרון קלסר. מים, משחת עמילן, סירופ סוכר, תמיסת מתיל תאית, תמיסת הידרוקסיפרופיל מתיל תאית, תמיסת פוליוויניל פירולידון, תמיסת אלכוהול פוליוויניל.
• חומר גלישה. תרסיס, עמילן, טלק.
• מילוי. סוכר, גלוקוז, לקטוז, נתרן כלורי, סידן פוספט.
• חומר סיכה. חומצה סטארית, פוליאתילן גליקול, פרפין.

ניתוח מודלים של שונות במחקר התחרותיות של המדינה

אחד הקריטריונים החשובים ביותר להערכת מצב המדינה, המעריך את רמת רווחתה והתפתחותה החברתית-כלכלית, הוא התחרותיות, כלומר מערכת נכסים הטמונה בכלכלה הלאומית, הקובעים את יכולתה של המדינה להתמודד עם מדינות אחרות. לאחר שקבענו את מקומה ותפקידה של המדינה בשוק העולמי, אנו יכולים לקבוע אסטרטגיה ברורה להבטיח ביטחון כלכלי בינלאומית, מכיוון שהיא המפתח ליחסים חיוביים בין רוסיה לכלל השחקנים בשוק העולמי: משקיעים, נושים, ממשלות מדינה.

כדי להשוות את רמת התחרותיות של מדינות, מדינות דורגות לפי מדדים מורכבים הכוללים אינדיקטורים משוקללים שונים. הבסיס למדדים אלה הוא גורמי המפתח המשפיעים על המצב הכלכלי, הפוליטי וכו '. מערכת מודלים ללימוד התחרותיות של המדינה מספקת שימוש בשיטות ניתוח סטטיסטיות מרובות משתנים (בפרט, ניתוח השונות (סטטיסטיקה), מידול אקונומטרי, קבלת החלטות) וכוללת את הצעדים העיקריים הבאים:

1. גיבוש מערכת אינדיקטורים-אינדיקטורים.
2. הערכה וחיזוי מדדים לתחרותיות במדינה.
3. השוואה בין אינדיקטורים ומדדים לתחרותיות של מדינות.

שקול עכשיו את תוכן הדגמים של כל אחד משלבי הקומפלקס הזה.

בשלב הראשון בעזרת שיטות לימוד מומחים, נוצרת קבוצה מוצדקת של אינדיקטורים כלכליים-אינדיקטורים להערכת יכולת התחרותיות של המדינה תוך התחשבות בפרטי התפתחותה על בסיס דירוגים בינלאומיים ונתונים של מחלקות סטטיסטיות המשקפות את מצב המערכת כולה ואת תהליכיה.הבחירה במדדים אלה מוצדקת על ידי הצורך לבחור את אלה שבאופן מלא ביותר מבחינת התרגול מאפשרים לקבוע את רמת המדינה, את האטרקטיביות שלה להשקעה ואת האפשרויות של לוקליזציה יחסית של איומים פוטנציאליים וחיים אמיתיים.

המדדים העיקריים-אינדיקטורים של מערכות דירוג בינלאומיות הם המדדים:

1. תחרות גלובלית (IGC).
2. חופש כלכלי (IES).
3. פיתוח אנושי (HDI).
4. תפיסות השחיתות (מדד המחירים לצרכן).
5. איומים פנימיים וחיצוניים.
6. פוטנציאל ההשפעה הבינלאומי (IPMV).

שלב שני היא מספקת הערכה וחיזוי של אינדיקטורים לתחרותיות המדינה על פי דירוגים בינלאומיים עבור 139 מדינות העולם שנחקרו.

שלב שלישי מספק השוואה בין תנאי התחרותיות של מדינות בשיטות מתאם וניתוח רגרסיה.

בעזרת תוצאות המחקר ניתן לקבוע את טיב התהליכים בכללותם ועל ידי מרכיבים פרטניים לתחרותיות של המדינה; בחן את ההשערה של השפעת גורמים ויחסיהם עם המתאימים רמת משמעות.

יישום מערך הדגמים המוצע יאפשר לא רק להעריך את המצב הקיים ברמת התחרותיות ואת האטרקטיביות של ההשקעות של מדינות, אלא גם לנתח את חולשות הניהול, למנוע טעויות של החלטות שגויות ולמנוע התפתחות משבר במדינה.