L'analyse de régression est une méthode statistique permettant d'étudier la dépendance d'une variable aléatoire

En modélisation statistique, l’analyse de régression est une étude utilisée pour évaluer la relation entre les variables. Cette méthode mathématique comprend de nombreuses autres méthodes pour modéliser et analyser plusieurs variables, lorsque l’accent est mis sur la relation entre la variable dépendante et une ou plusieurs variables indépendantes. Plus précisément, l'analyse de régression aide à comprendre comment une valeur typique d'une variable dépendante change si l'une des variables indépendantes change, alors que les autres variables indépendantes restent fixes.

Dans tous les cas, l'estimation cible est une fonction de variables indépendantes et s'appelle la fonction de régression. En analyse de régression, il est également intéressant de caractériser l'évolution de la variable dépendante en fonction de la régression, ce qui peut être décrit à l'aide d'une distribution de probabilité.

Tâches d'analyse de régression

Cette méthode de recherche statistique est largement utilisée pour la prévision, lorsque son utilisation présente un avantage important mais peut parfois conduire à des illusions ou à de fausses relations. Il est donc recommandé de l’utiliser avec précaution dans ce numéro, car, par exemple, corrélation ne signifie pas une relation de cause à effet.

Un grand nombre de méthodes ont été développées pour effectuer une analyse de régression, telles que la régression linéaire et la méthode des moindres carrés ordinaires, qui sont paramétriques. Leur essence est que la fonction de régression est définie en termes d'un nombre fini de paramètres inconnus estimés à partir des données. La régression non paramétrique permet à ses fonctions de se situer dans un certain ensemble de fonctions, qui peuvent être de dimension infinie.

En tant que méthode de recherche statistique, l’analyse de régression en pratique dépend de la forme du processus de génération de données et de son lien avec l’approche de régression. Étant donné que la forme réelle du processus de données génère généralement un nombre inconnu, l'analyse de régression des données dépend souvent, dans une certaine mesure, des hypothèses retenues sur ce processus. Ces hypothèses sont parfois vérifiées si suffisamment de données sont disponibles. Les modèles de régression sont souvent utiles même lorsque les hypothèses sont modérément violées, bien qu'elles ne puissent fonctionner avec une efficacité maximale.

Dans un sens plus étroit, la régression peut porter spécifiquement sur l'évaluation des variables à réponse continue, par opposition aux variables à réponse discrète utilisées dans la classification. Le cas d'une variable de sortie continue est également appelé régression métrique afin de la distinguer des problèmes connexes.

L'histoire

La plus ancienne forme de régression est la méthode des moindres carrés bien connue. Il a été publié par Legendre en 1805 et Gauss en 1809. Legendre et Gauss ont appliqué la méthode à la tâche consistant à déterminer à partir d'observations astronomiques les orbites de corps autour du Soleil (principalement des comètes, mais de nouvelles planètes récemment découvertes). Gauss a publié un développement ultérieur de la théorie des moindres carrés en 1821, incluant une version du théorème de Gauss-Markov.

Le terme «régression» a été inventé par Francis Galton au 19ème siècle pour décrire un phénomène biologique. En fin de compte, la croissance des descendants résultant de la croissance des ancêtres régressait généralement jusqu'à la moyenne normale.Pour Galton, la régression n’avait que cette signification biologique, mais ses travaux ont ensuite été poursuivis par Udney Yule et Karl Pearson et amenés à un contexte statistique plus général. Dans les travaux de Yule et Pearson, la distribution conjointe des variables de réponse et des variables explicatives est considérée comme gaussienne. Cette hypothèse a été rejetée par Fisher dans les travaux de 1922 et 1925. Fisher a suggéré que la distribution conditionnelle de la variable de réponse était gaussienne, alors que la distribution conjointe ne devrait pas l'être. À cet égard, l’hypothèse de Fischer est plus proche de la formulation de 1821 de Gauss. Jusqu'en 1970, il fallait parfois jusqu'à 24 heures pour obtenir le résultat d'une analyse de régression.

Les méthodes d'analyse de régression restent un domaine de recherche actif. Au cours des dernières décennies, de nouvelles méthodes ont été développées pour une régression fiable; régression impliquant des réponses corrélées; méthodes de régression tenant compte de divers types de données manquantes; régression non paramétrique; Méthodes de régression bayésienne; régressions dans lesquelles les variables prédictives sont mesurées avec une erreur; les régressions avec plus de prédicteurs que les observations, ainsi que les inférences causales avec la régression.

Modèles de régression

Les modèles d'analyse de régression incluent les variables suivantes:

• Paramètres inconnus, appelés bêta, qui peuvent être un scalaire ou un vecteur.
• Variables indépendantes, X.
• Variables dépendantes, Y.

Dans divers domaines scientifiques où l’analyse de régression est appliquée, divers termes sont utilisés à la place de variables dépendantes et indépendantes, mais dans tous les cas, le modèle de régression relie Y aux fonctions X et β.

L'approximation prend généralement la forme E (Y | X) = F (X, β). Pour effectuer une analyse de régression, le type de fonction f doit être déterminé. Moins communément, il est basé sur la connaissance de la relation entre Y et X qui ne repose pas sur des données. Si de telles connaissances ne sont pas disponibles, une forme F souple ou pratique est choisie.

Variable dépendante Y

Supposons maintenant que le vecteur de paramètres inconnus β ait la longueur k. Pour effectuer une analyse de régression, l'utilisateur doit fournir des informations sur la variable dépendante Y:

• S'il existe N points de données de la forme (Y, X), où N

• Si exactement N = K est observé et que la fonction F est linéaire, l'équation Y = F (X, β) peut être résolue exactement et non approximativement. Ceci se réduit à la résolution d'un ensemble de N-équations à N inconnues (éléments de β), qui a une solution unique tant que X est linéairement indépendant. Si F est non linéaire, la solution peut ne pas exister ou plusieurs solutions peuvent exister.
• Le plus commun est la situation où N> points aux données sont observées. Dans ce cas, les données contiennent suffisamment d'informations pour évaluer la valeur unique de β qui correspond le mieux aux données, et le modèle de régression, lorsqu'il est appliqué aux données, peut être considéré comme un système surdéterminé dans β.

Dans ce dernier cas, l’analyse de régression fournit des outils pour:

• Recherche de solutions pour les paramètres inconnus β, qui réduiront par exemple la distance entre les valeurs mesurées et prédites de Y.
• Sous certaines hypothèses statistiques, l’analyse de régression utilise des informations excédentaires pour fournir des informations statistiques sur les paramètres inconnus β et les valeurs prédites de la variable dépendante Y.

Nombre nécessaire de mesures indépendantes

Prenons un modèle de régression comportant trois paramètres inconnus: β₀, β₁ et β₂. Supposons que l'expérimentateur effectue 10 mesures dans la même valeur de la variable indépendante du vecteur X.Dans ce cas, l'analyse de régression ne fournit pas un ensemble unique de valeurs. La meilleure chose à faire est d’évaluer l’écart moyen et standard de la variable dépendante Y. En mesurant deux valeurs X différentes de la même manière, vous pouvez obtenir suffisamment de données pour une régression à deux inconnues, mais pas pour trois inconnues ou plus.

Si les mesures de l'expérimentateur ont été effectuées à trois valeurs différentes de la variable indépendante du vecteur X, l'analyse de régression fournira un ensemble unique d'estimations pour trois paramètres inconnus dans β.

Dans le cas d'une régression linéaire générale, l'énoncé précédent équivaut à exiger que la matrice X^TX est réversible.

Hypothèses statistiques

Lorsque le nombre de mesures N est supérieur au nombre de paramètres inconnus k et à l'erreur de mesure ε_jeensuite, en règle générale, l’excès d’informations contenues dans les mesures est ensuite distribué et utilisé pour les prévisions statistiques concernant des paramètres inconnus. Cet excès d'information s'appelle le degré de liberté de régression.

Hypothèses fondamentales

Les hypothèses classiques pour l'analyse de régression comprennent:

• L'échantillon est représentatif de la prédiction d'inférence.
• L'erreur est une variable aléatoire avec une valeur moyenne de zéro, conditionnée par les variables explicatives.
• Les variables indépendantes sont mesurées sans erreur.
• En tant que variables indépendantes (prédicteurs), elles sont linéairement indépendantes, c'est-à-dire qu'il est impossible d'exprimer un prédicteur sous la forme d'une combinaison linéaire des autres.
• Les erreurs ne sont pas corrélées, c’est-à-dire que la matrice de covariance des erreurs diagonales et chaque élément non nul sont la variance de l’erreur.
• La variance de l'erreur est constante en fonction des observations (homoscédasticité). Sinon, vous pouvez utiliser la méthode des moindres carrés pondérés ou d'autres méthodes.

Ces conditions suffisantes pour l'estimation par les moindres carrés possèdent les propriétés requises. En particulier, ces hypothèses impliquent que les estimations de paramètres seront objectives, cohérentes et efficaces, en particulier lorsqu'elles seront prises en compte dans la classe des estimations linéaires. Il est important de noter que la preuve satisfait rarement aux conditions. C'est-à-dire que la méthode est utilisée même si les hypothèses ne sont pas vraies. Une variation des hypothèses peut parfois être utilisée pour mesurer l'utilité de ce modèle. Beaucoup de ces hypothèses peuvent être atténuées par des méthodes plus avancées. Les rapports d'analyse statistique incluent généralement l'analyse de tests basés sur des données d'échantillon et une méthodologie pour l'utilité du modèle.

De plus, les variables se réfèrent dans certains cas à des valeurs mesurées à des points précis. Il peut exister des tendances spatiales et une autocorrélation spatiale dans les variables qui violent les hypothèses statistiques. La régression pondérée géographique est la seule méthode qui traite de telles données.

Analyse de régression linéaire

En régression linéaire, une caractéristique est que la variable dépendante, qui est Y_jeest une combinaison linéaire de paramètres. Par exemple, dans une régression linéaire simple, une variable indépendante, x, est utilisée pour modéliser des points n_jeet deux paramètres, β₀ et β₁.

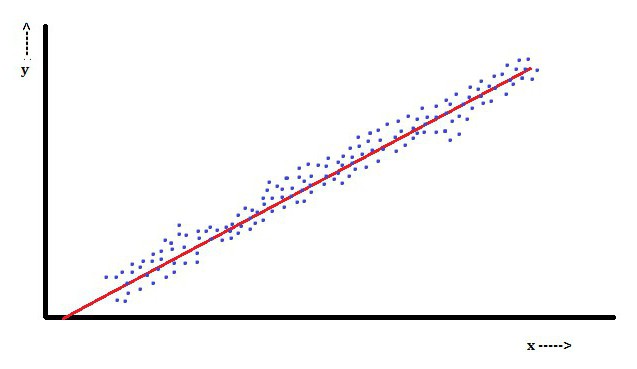
Avec la régression linéaire multiple, il existe plusieurs variables indépendantes ou leurs fonctions.

Avec un échantillonnage aléatoire d'une population, ses paramètres permettent d'obtenir un exemple de modèle de régression linéaire.

Dans cet aspect, la méthode des moindres carrés est la plus populaire. En l'utilisant, on obtient des estimations de paramètres qui minimisent la somme des résidus au carré. Ce type de minimisation (caractéristique d'une régression linéaire) de cette fonction conduit à un ensemble d'équations normales et à un ensemble d'équations linéaires avec des paramètres résolus pour obtenir des estimations de paramètres.

En supposant en outre que l'erreur de la population se propage généralement, le chercheur peut utiliser ces estimations d'erreur standard pour créer des intervalles de confiance et tester des hypothèses concernant ses paramètres.

Analyse de régression non linéaire

Un exemple où la fonction n'est pas linéaire par rapport aux paramètres indique que la somme des carrés doit être minimisée à l'aide d'une procédure itérative. Cela introduit de nombreuses complications qui déterminent les différences entre les méthodes des moindres carrés linéaires et non linéaires. Par conséquent, les résultats de l'analyse de régression utilisant la méthode non linéaire sont parfois imprévisibles.

Calcul de la puissance et de la taille de l'échantillon

Ici, en règle générale, il n’existe pas de méthodes cohérentes concernant le nombre d’observations par rapport au nombre de variables indépendantes du modèle. La première règle proposée par Good et Hardin ressemble à N = t ^ n, où N est la taille de l’échantillon, n le nombre de variables indépendantes et t le nombre d’observations nécessaires pour obtenir la précision souhaitée si le modèle n’avait qu’une seule variable indépendante. Par exemple, un chercheur construit un modèle de régression linéaire à l'aide d'un ensemble de données contenant 1 000 patients (N). Si le chercheur décide que cinq observations sont nécessaires pour déterminer avec précision la droite (m), le nombre maximal de variables indépendantes que le modèle peut prendre en charge est de 4.

Autres méthodes

Bien que les paramètres du modèle de régression soient généralement estimés à l'aide de la méthode des moindres carrés, il existe d'autres méthodes beaucoup moins utilisées. Par exemple, ce sont les méthodes suivantes:

• Méthodes bayésiennes (par exemple, méthode de régression linéaire bayésienne).
• Régression en pourcentage, utilisée pour les situations dans lesquelles une réduction des erreurs en pourcentage est jugée plus appropriée.
• Les plus petits écarts absolus, qui sont plus stables en présence de valeurs aberrantes conduisant à une régression quantile.
• Régression non paramétrique, nécessitant un grand nombre d'observations et de calculs.
• Distance de la métrique d'apprentissage étudiée à la recherche d'une distance métrique significative dans un espace d'entrée donné.

Logiciel

Tous les principaux logiciels de statistiques sont réalisés à l'aide d'une analyse de régression des moindres carrés. Une régression linéaire simple et une analyse de régression multiple peuvent être utilisées dans certaines applications de tableur, ainsi que sur certaines calculatrices. Bien que de nombreux progiciels statistiques puissent effectuer différents types de régression fiable et non paramétrique, ces méthodes sont moins normalisées. différents logiciels implémentent différentes méthodes. Un logiciel de régression spécialisé a été développé pour être utilisé dans des domaines tels que l'analyse par examen et la neuroimagerie.