Nivelul de semnificație al statisticilor este un indicator important care reflectă gradul de încredere în acuratețea și adevărul datelor primite (prezise). Conceptul este utilizat pe scară largă în diverse domenii: de la efectuarea cercetărilor sociologice, până la testarea statistică a ipotezelor științifice.

definiție
Nivelul de semnificație statistică (sau rezultat semnificativ statistic) arată care este probabilitatea apariției accidentale a indicatorilor studiați. Semnificația statistică generală a fenomenului este exprimată prin coeficientul p-valoare (p-nivel). În orice experiment sau observație, este probabil ca datele obținute să se datoreze erorilor de eșantionare. Acest lucru este valabil mai ales pentru sociologie.
Adică, o statistică este semnificativă statistic a cărei probabilitate de apariție accidentală este extrem de mică sau tinde spre extreme. Extrem în acest context este considerat gradul de deviere a statisticilor de la ipoteza nulă (ipoteză care este verificată în concordanță cu datele din eșantion obținute). În practica științifică, nivelul de semnificație este ales înainte de colectarea datelor și, de regulă, coeficientul său este de 0,05 (5%). Pentru sistemele în care valorile exacte sunt extrem de importante, acest indicator poate fi de 0,01 (1%) sau mai puțin.
anamneză
Conceptul de nivel de semnificație a fost introdus de statisticianul și geneticianul britanic Ronald Fisher în 1925, când a dezvoltat o metodologie pentru testarea ipotezelor statistice. Când analizăm un proces, există o anumită probabilitate a anumitor fenomene. Dificultăți apar atunci când lucrați cu probabilități mici (sau nu evidente) de procente care se încadrează în conceptul de „eroare de măsurare”.
Când lucrează cu statistici care nu sunt suficient de specifice pentru a verifica, oamenii de știință s-au confruntat cu problema ipotezei nule, care „interferează” cu cantități mici. Fisher a sugerat definirea pentru astfel de sisteme probabilitatea evenimentelor 5% (0,05) ca o felie selectivă convenabilă, ceea ce vă permite să respingeți ipoteza nulă în calcule.
Introducerea unui coeficient fix
În 1933, oamenii de știință Jerzy Neumann și Egon Pearson în lucrările lor au recomandat dinainte (înainte de culegerea datelor) să stabilească un anumit nivel de semnificație. Exemple de utilizare a acestor reguli sunt clar vizibile în timpul alegerilor. Să presupunem că există doi candidați, dintre care unul este foarte popular, iar al doilea este puțin cunoscut. Evident, primul candidat câștigă alegerile, iar șansele celui de-al doilea tind să fie zero. Se străduiesc - dar nu sunt egali: există întotdeauna posibilitatea de forță majoră, informații senzaționale, decizii neașteptate care pot schimba rezultatele alegerilor prevăzute.
Neumann și Pearson au convenit că nivelul de semnificație propus de Fisher de 0,05 (notat cu simbolul α) este cel mai convenabil. Cu toate acestea, însuși Fisher în 1956 s-a opus fixării acestei valori. El a crezut că nivelul de α trebuie stabilit în conformitate cu circumstanțe specifice. De exemplu, în fizica particulelor este 0,01.

nivelul de semnificație p
Termenul p-valoare a fost folosit pentru prima dată în activitatea lui Brownley în 1960. Nivelul P (valoarea p) este un indicator care este invers legat de adevărul rezultatelor. Cea mai mare valoare a coeficientului p corespunde celui mai mic nivel de încredere în eșantionul de dependență dintre variabile.
Această valoare reflectă probabilitatea erorilor asociate cu interpretarea rezultatelor. Să presupunem că nivelul p = 0,05 (1/20). Acesta arată probabilitatea de cinci procente ca relația dintre variabilele găsite în eșantion să fie doar o caracteristică aleatoare a eșantionului.Adică, dacă această dependență este absentă, atunci cu repetate astfel de experimente, în medie, la fiecare douăzeci de studii, se poate aștepta o dependență identică sau mai mare între variabile. Adesea, nivelul p este considerat „marja acceptabilă” a nivelului de eroare.
Apropo, valoarea p nu poate reflecta relația reală dintre variabile, ci arată doar o anumită valoare medie în cadrul presupunerilor. În special, analiza finală a datelor va depinde și de valorile selectate ale acestui coeficient. Cu un nivel p = 0,05, vor exista unele rezultate, iar cu un coeficient de 0,01, altele.

Testarea ipotezelor statistice
Nivelul de semnificație statistică este deosebit de important la testarea ipotezelor. De exemplu, atunci când se calculează un test pe două fețe, aria de respingere este împărțită în mod egal la ambele capete ale distribuției eșantionului (în raport cu coordonata zero) și se calculează adevărul datelor.
Să presupunem că, atunci când monitorizăm un anumit proces (fenomen), s-a dovedit că noile informații statistice indică mici modificări în raport cu valorile anterioare. Mai mult decât atât, discrepanțele în rezultate sunt mici, nu sunt evidente, dar importante pentru studiu. Dilema apare înaintea specialistului: au loc schimbările cu adevărat sau sunt aceste erori de eșantionare (măsurători inexacte)?
În acest caz, ipoteza nulă este fie utilizată, fie respinsă (toate sunt atribuite unei erori, sau modificarea sistemului este recunoscută ca un fapt complet). Procesul de soluționare a problemei se bazează pe raportul dintre semnificația statistică totală (valoarea p) și nivelul semnificației (α). Dacă nivelul p <α, atunci ipoteza nulă este respinsă. Cu cât valoarea p este mai mică, cu atât este mai semnificativă statistica testului.
Valori utilizate
Nivelul de semnificație depinde de materialul analizat. În practică, sunt utilizate următoarele valori fixe:
- α = 0,1 (sau 10%);
- α = 0,05 (sau 5%);
- α = 0,01 (sau 1%);
- α = 0,001 (sau 0,1%).
Cu cât sunt necesare calcule mai precise, cu atât este mai mic coeficientul α. Desigur, prognozele statistice în fizică, chimie, produse farmaceutice, genetică necesită o precizie mai mare decât în științele politice, în sociologie.

Praguri de relevanță în anumite domenii
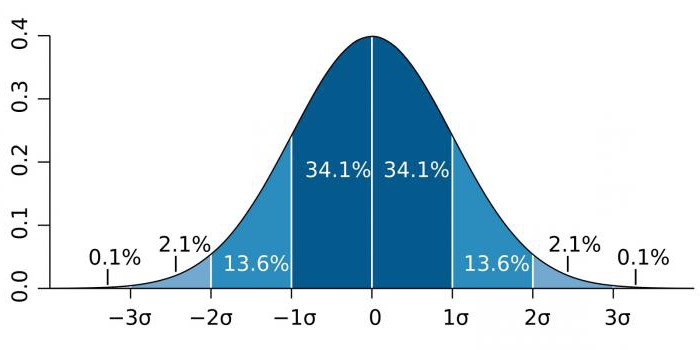
În domenii de înaltă precizie, cum ar fi fizica particulelor și activitățile de fabricație, semnificația statistică este adesea exprimată ca raportul deviației standard (notat de coeficientul sigma - σ) în raport cu distribuția probabilității normale (distribuția Gaussiană). σ este un indicator statistic care determină dispersia valorilor unei anumite valori în raport cu așteptările matematice. Folosit pentru a reprezenta probabilitatea evenimentelor.
În funcție de domeniul de cunoștințe, coeficientul σ variază mult. De exemplu, când se prezice existența bosonului Higgs, parametrul σ este de cinci (σ = 5), ceea ce corespunde valorii p-valoare = 1 / 3,5 milioane. În studiile asupra genomilor, nivelul de semnificație poate fi de 5 × 10.-8care nu sunt neobișnuite pentru acest domeniu.
eficacitate
Rețineți că coeficienții α și valoarea p nu sunt caracteristici exacte. Oricare ar fi nivelul de semnificație în statisticile fenomenului studiat, nu este o bază necondiționată pentru acceptarea ipotezei. De exemplu, cu cât valoarea α este mai mică, cu atât este mai mare șansa ca ipoteza stabilită să fie semnificativă. Cu toate acestea, există riscul de eroare, ceea ce reduce puterea statistică (semnificația) studiului.
Cercetătorii care se concentrează exclusiv pe rezultate semnificative din punct de vedere statistic pot primi concluzii eronate. În același timp, este dificil să le verifici dublu munca, deoarece folosesc presupuneri (care, de fapt, sunt valorile α și p). Prin urmare, se recomandă întotdeauna, împreună cu calculul semnificației statistice, să se determine un alt indicator - amploarea efectului statistic. Mărimea unui efect este o măsură cantitativă a forței unui efect.
