"Stokastinen" on sana, jota fyysikot, matemaatikot ja muut tutkijat käyttävät kuvaamaan prosesseja, joilla on sattumanvarainen elementti. Sen alkuperä on muinaiskreikkalaista. Käännettynä se tarkoittaa "osaa arvata".
Sana "stokastinen" merkitys

"Stokastinen" on käsite, jota käytetään monilla tieteen aloilla. Se tarkoittaa sattumanvaraisuutta, sattumanvaraisuutta, jonkin epävarmuutta. Aristoteleen etiikassa (hänen veistoksellinen muotokuvansa on esitetty yllä) käsite "stokastinen" on määritelmä, joka viittaa kykyyn arvata. Tietenkin, matemaatikot käyttivät sitä sillä perusteella, että sattuman elementti ilmestyy juuri tarvittaessa arvaamaan. Sana "stokastinen" on käsite, joka on määritelty uudessa kansainvälisessä sanakirjassa "olettamukseksi".
Siten voidaan huomata, että tämän käsitteen tekninen merkitys ei vastaa tarkalleen sen sanastoa (leksikkoa) merkitystä. Jotkut kirjoittajat käyttävät ilmausta "stokastinen prosessi" synonyyminä käsitteelle "satunnainen prosessi".
Stokastisuus matematiikassa

Tämän termin käyttö matematiikassa on nykyään yleistä. Esimerkiksi todennäköisyysteoriassa on sellainen käsite kuin stokastinen prosessi. Sen tulosta ei voida määrittää järjestelmän alkutilan perusteella.
Käsitteen "stokastisuus" käyttö matematiikassa johtuu Vladislav Bortskevitšin teoksista. Se oli hän, joka käytti termiä tarkoituksessa "esittää hypoteeseja". Matematiikassa, etenkin tämän tieteen sellaisessa osassa kuin todennäköisyysteoria, satunnaisen tutkimuksen kentällä on tärkeä rooli. On esimerkiksi sellainen asia kuin stokastinen matriisi. Tämän matriisin sarakkeet tai rivit muodostavat yhden.
Stokastinen matematiikka (taloudellinen)
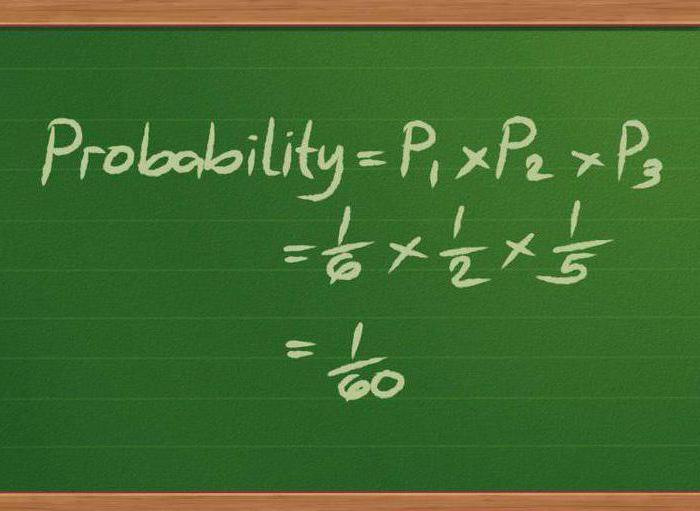
Tämä matematiikan osa analysoi epävarmuuden olosuhteissa toimivia rahoitusrakenteita. Sen tarkoituksena on löytää järkevimmät menetelmät rahoitusvarojen ja rakenteiden hallitsemiseksi ottaen huomioon tekijät, kuten stokastinen kehitys, riski, aika jne.
Tieteessä on tapana erottaa seuraavat rakenteet ja esineet, joita käytetään koko talousmatematiikassa:
- yritykset (esimerkiksi yritykset);
- yksilöitä;
- välittäjärakenteet (eläkerahastot, pankit);
- rahoitusmarkkinat.
Stokastisen taloudellisen matematiikan päätarkoituksena on juuri viimeinen niistä. Tämä osa perustuu sellaisiin tieteenaloihin kuin satunnaisprosessien tilastot, satunnaisprosessien teoria jne.
Tällä hetkellä jopa tiedestä kaukana olevista ihmisistä on lukuisista media- ja uutisista ja julkaisuista hyvin tiedossa, että ns. Globaalien rahoitusindeksien (esimerkiksi Dow Jones -indeksi) arvot muuttuvat osakehinnoin satunnaisesti. L. Bachelier yritti ensimmäisenä kuvailla matematiikan avulla osakekurssien kehitystä. Hänen stokastinen menetelmä perustuu todennäköisyysteoriaan. Tätä yritystä esittelevä L. Bachelierin väitöskirja julkaistiin vuonna 1900. Tutkija on todistanut kaavan, jota nykyään kutsutaan käypään arvoon perustuvaksi laskuvaihtoehtoksi. Se kuvastaa stokastista todennäköisyyttä.
Tärkeät ideat, jotka myöhemmin johtivat tehokkaan markkiteorian syntyyn, esitettiin M. Kendallin vuonna 1953 julkaisemassa työssä. Tämä artikkeli käsittelee osakekurssien dynamiikkaa. Tutkija kuvaa sitä stokastisilla prosesseilla.
Stokastisuus fysiikassa
Kiitos fyysikoille E. Fermi, S. Ulam, N. Metropolis ja D.Neumann on laajalti käytetty Monte Carlo -menetelmä. Sen nimi tulee kasinosta, joka sijaitsee samassa kaupungissa maassa kuten Monaco. Juuri täällä setä Ulam lainasi rahaa peliin. Toistamisen luonteen ja mahdollisuuden käyttäminen prosessien tutkimiseen on samanlaista kuin kasinolla tapahtuu.

Tätä mallinnusmenetelmää sovellettaessa etsitään ensin todennäköisyyden analogia. Ennen tätä mallintaminen suoritettiin vastakkaiseen suuntaan: sitä käytettiin varmentamaan aikaisemmin saadun deterministisen ongelman tulos. Vaikka samanlaiset lähestymistavat olivat olemassa ennen Monte Carlo -menetelmän löytämistä, ne eivät olleet suosittuja ja yleisiä.
Enrico Fermi käytti vuonna 1930 stokastisia tekniikoita neutronin ominaisuuksien laskemiseen, joka oli juuri löydetty tuolloin. Monte Carlo -menetelmiä käytettiin myöhemmin Manhattan-projektissa, vaikka tietokoneiden ominaisuudet olivat tuolloin rajoitetusti huomattavat. Tästä syystä niistä tuli laajalle levinnyttä vasta tietokoneiden ilmestymisen jälkeen.
Stokastiset signaalit
Säännöllisillä ja stokastisilla signaaleilla on erilaiset aaltomuodot. Jos mittaamme jälkimmäisen, saamme värähtelyt, joilla on uusi muoto, joka on erilainen kuin edellinen, mutta osoittaa tietyn samanlaisuuden olennaisissa piirteissä. Esimerkki stokastisesta signaalista on meriaallon värähtelyjen tallennus.
Miksi on tarpeen puhua näistä melko epätavallisista signaaleista? Tosiasia, että automaattisten järjestelmien tutkimuksessa ne ovat jopa yleisempiä kuin ennustettiin.
Stokastisuus ja tekoäly
Stokastiset tekoälyohjelmat toimivat todennäköisyysmenetelmillä. Esimerkkeinä voidaan mainita algoritmit, kuten stokastinen optimointi tai hermoverkot. Sama pätee simuloituihin hehkutus- ja geneettisiin algoritmeihin. Kaikissa näissä tapauksissa stokastisuus voi sisältyä ongelmaan sinänsä tai jonkin suunnittelemiseen epävarmuuden olosuhteissa. Mallinnusaineen deterministinen ympäristö on yksinkertaisempi kuin stokastinen.

Joten, kuten näemme, meitä kiinnostavaa käsitettä käytetään monilla tieteen aloilla. Olemme luetelleet ja luonnehtineet vain sen soveltamisalat. Kaikkien näiden prosessien tutkiminen on mielestäni erittäin tärkeää ja asiaankuuluvaa. Siksi meitä kiinnostavaa käsitettä käytetään todennäköisesti jo pitkään tieteessä.








