Nell'articolo considereremo il concetto di "probabilità di un evento accidentale". È noto che in varie sfere dell'attività umana vi sono fenomeni che non possono essere previsti con precisione. Quindi, ad esempio, il volume delle vendite dei prodotti dipende sia dalle mutevoli esigenze dei clienti, sia da altre sfumature che non è possibile prendere in considerazione. Ecco perché, creando produzione e realizzando vendite, i proprietari devono prevedere il risultato delle loro attività sulla base dell'esperienza personale o di un'analoga competenza di altre persone.
Per valutare l'evento in questione, è necessario prendere in considerazione o creare in modo speciale le condizioni in cui è registrato. Tali azioni sono chiamate esperienza o esperimento. Nel suo processo, ci sono possibili episodi che vengono chiamati casuali, se alla fine possono aver luogo o meno, nonché fenomeni affidabili che sorgono a seguito della pratica.
Studiamo la probabilità di un evento usando esempi. Ad esempio, la nevicata a Mosca il 25 novembre è considerata un episodio casuale. L'alba di tutti i giorni è un fenomeno affidabile e la nevicata all'equatore della neve è considerata una curiosità impossibile. Uno dei compiti più importanti nella teoria della probabilità è il problema di determinare una misura quantitativa della possibilità che si verifichi un evento.
probabilità
La probabilità è il grado (valutazione quantitativa, misura relativa) della possibilità che si verifichi un evento. Quando i motivi per una possibile occorrenza nella realtà sono superati da argomenti contrastanti, questo caso è chiamato probabile. Altrimenti, si chiama dubbio o incredibile.
La preponderanza della base negativa su quella positiva, e viceversa, può essere in vari gradi, a causa della quale l'inammissibilità (o ammissibilità) è minore o maggiore. Per questo motivo, la probabilità di un evento è spesso percepita a un livello di prima classe, specialmente in quei passaggi in cui è estremamente difficile o impossibile dare una valutazione quantitativa precisa. Naturalmente, sono possibili diverse gradazioni dei livelli di probabilità.
Analisi di probabilità
A proposito, la probabilità di eventi indipendenti ha parametri speciali. E sondare una possibilità da una posizione matematica completa una disciplina specifica: la teoria della probabilità. In questo insegnamento e nelle statistiche matematiche, il concetto di ammissibilità è ufficializzato come una descrizione numerica dell'episodio (una misura probabilistica o il suo significato).
In realtà, questa è una misura in molti casi (sottoinsiemi di molti fenomeni elementari), acquisendo valori da 0 a 1:
- un valore di 1 corrisponde a un episodio valido;
- un fatto impossibile ha zero possibilità (il contrario è quasi sempre falso).
Se il verificarsi del fenomeno è p, il rischio di inerzia è 1-p. Supponiamo che la probabilità ½ significhi la stessa possibilità di occorrenza e non occorrenza del caso.

Dichiarazione di possibilità
Test, evento, probabilità: queste variabili sono strettamente legate dalla scienza. Una definizione tipica di caso si basa sul concetto di equiprobabilità dei risultati.
Il rapporto tra il numero di finali che contribuiscono a questo evento e il numero totale di finali ugualmente possibili è un'opportunità. Ad esempio, l'ammissibilità di una “coda” o di un'aquila che cade se un lancio involontario di un centesimo è 1/2, se si calcola che solo questi due percorsi sono ugualmente probabili.

Questa classica definizione di casualità può essere generalizzata al caso di un numero inesauribile di valori potenziali.Ad esempio, se un fenomeno può verificarsi con uguale ammissibilità in qualsiasi punto (il numero di punti è illimitato) di una regione locale del piano (spazio), il rischio che si verifichi in una determinata parte di questa sfera accettabile corrisponde al rapporto dell'area (volume) di questa parte all'area (volume) dell'area di tutti i punti possibili.
collegamento
La probabilità di un evento può essere determinata empiricamente. Ciò è dovuto alla frequenza di insorgenza dell'episodio basata sul fatto che con un numero impressionante di test, la frequenza dovrebbe perseguire un grado oggettivo di possibilità di questo precedente.
Nell'attuale presentazione della teoria della probabilità, la probabilità viene rivelata assiomaticamente, come un fatto particolare della teoria astratta della misura di un insieme. Tuttavia, tra l'ammissibilità che esprime il grado di realtà del verificarsi del fenomeno e la misura astratta, il collegamento è precisamente la frequenza del suo tracciamento.

Naturalmente, è possibile che si verifichi un evento in vari processi. Un'interpretazione stocastica di alcuni fenomeni è ampiamente diffusa nella scienza moderna, in particolare nell'econometria, nella fisica statistica dei sistemi termodinamici (visibili), dove anche nel caso di una descrizione classica deterministica del moto delle particelle, una descrizione concreta di tutta la loro struttura non sembra conveniente e praticamente possibile. Nella fisica quantistica, i processi caratterizzati stessi hanno una natura stocastica.
Evento casuale
Naturalmente, la probabilità che si verifichi un evento in ogni processo incontrollato è alta. Che cos'è una contingenza? Questo è un sottoinsieme dei numerosi risultati di un esperimento accidentale. Se un'indagine casuale viene ripetuta più volte, la frequenza del verificarsi di un fatto serve da valutazione della sua ammissibilità. 
Un fenomeno involontario che non si verifica mai a seguito di un esperimento involontario si chiama impossibile. Un episodio casuale, che viene sempre realizzato a seguito di un esperimento inaspettato, si chiama affidabile. E come è caratterizzata la probabilità di eventi indipendenti? È noto che due fatti casuali sono definiti indipendenti se l'apparenza di uno di essi non cambia la ricevibilità dell'aspetto dell'altro.
Un evento casuale è un evento regolare creato generando funzioni involontarie con sostituzione di variabili casuali in variabili. La normale funzione di generare un numero della lotteria è svolta da strumenti informatici.
definizione
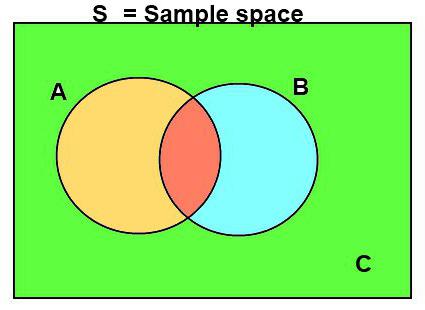
Un episodio matematicamente casuale è un sottoinsieme dello spazio degli esiti elementari di una sperimentazione involontaria. Questo è un elemento di sigma-algebra o algebra - F, che a sua volta è impostato in modo evidente e insieme allo spazio dei fenomeni più semplici "Omega" e la probabilità P forma uno spazio di probabilità.
Contesto del concetto di caso
La probabilità di un evento accidentale è stata spesso studiata. In generale, l'emergere del concetto di fortuna è stato storicamente associato al gioco d'azzardo, in particolare ai dadi. Prima dell'emergere di questo concetto, sono state principalmente delineate le attività combinatorie di calcolo del numero di potenziali esiti quando si lancia un paio di dadi, nonché l'emissione della distribuzione delle scommesse tra i partecipanti quando il gioco è terminato prima del previsto.
Il vescovo Vibold della città di Cambrai nel 960 decise i primi rebus lanciando tre dadi. Ha contato 56 specie. Tuttavia, questo numero in realtà non riproduce la somma di metodi ugualmente possibili, poiché ciascuna delle sue 56 versioni può essere eseguita da un numero diverso di ricevimenti.
La probabilità di un evento accidentale fu studiata nella prima metà del 13 ° secolo da Richard de Fornival. Nonostante citi anche il numero 56, riflette nel pensiero che lo stesso numero di punti su tre ossa può essere ottenuto con sei metodi.
Sulla base del suo ragionamento, è già possibile stabilire che il numero di opzioni ugualmente accessibili è 216. Successivamente, molti non hanno risolto il problema in modo corretto.Per la prima volta, Gallileo Galilei ha calcolato il numero di risultati ugualmente accessibili quando ha lanciato tre ossa: ha aumentato le sei (il numero di versioni della perdita di un osso) al grado 3 (il numero di ossa). Ha anche compilato una tabella del numero di opzioni per l'estrazione di varie quantità di punti.
Speriamo che il nostro articolo ti abbia pienamente informato della probabilità di un evento casuale.








