Нивото на значимост в статистиката е важен показател, отразяващ степента на увереност в точността и истинността на получените (прогнозираните) данни. Концепцията е широко използвана в различни области: от провеждане на социологически изследвания, до статистическо изпитване на научни хипотези.

дефиниция
Нивото на статистическа значимост (или статистически значим резултат) показва каква е вероятността за случайно възникване на изследваните показатели. Общата статистическа значимост на явлението се изразява чрез коефициента p-стойност (p-ниво). При всеки експеримент или наблюдение е вероятно получените данни да се дължат на грешки в извадката. Това важи особено за социологията.
Тоест, статистически е статистически значима, чиято вероятност от случайно настъпване е изключително малка или има тенденция към крайности. Изключителна в този контекст се счита за степента на отклонение на статистиката от нулевата хипотеза (хипотеза, която се проверява за съответствие с получените данни от извадката). В научната практика нивото на значимост се избира преди събирането на данни и като правило неговият коефициент е 0,05 (5%). За системи, където точните стойности са изключително важни, този показател може да бъде 0,01 (1%) или по-малко.
история на заболяването
Концепцията за ниво на значимост е въведена от британския статистик и генетик Роналд Фишър през 1925 г., когато той разработва методология за тестване на статистически хипотези. При анализиране на даден процес има определена вероятност за определени явления. Затруднения възникват при работа с малки (или не очевидни) проценти вероятности, които попадат под понятието „грешка в измерването“.
Когато работят със статистически данни, които не са достатъчно конкретни за проверка, учените са изправени пред проблема с нулевата хипотеза, която „се намесва“ в малки количества. Фишър предложи да се определят такива системи вероятност от събития 5% (0,05) като удобна селективна част, която ви позволява да отхвърлите нулевата хипотеза в изчисленията.
Въвеждането на фиксиран коефициент
През 1933 г. учените Йежи Нойман и Егон Пиърсън в своите разработки препоръчват предварително (преди събирането на данни), за да установят определено ниво на значимост. Примерите за използването на тези правила са ясно видими по време на изборите. Да предположим, че има двама кандидати, единият от които е много популярен, а вторият е малко известен. Очевидно първият кандидат печели изборите, а шансовете на втория имат тенденция към нула. Те се стремят - но не са равни: винаги има вероятност от непреодолима сила, сензационна информация, неочаквани решения, които могат да променят прогнозираните изборни резултати.
Нойман и Пиърсън се съгласиха, че предложеното от Фишър ниво на значимост 0,05 (обозначено със символа α) е най-удобно. Самият Фишър през 1956 г. обаче се противопостави на фиксирането на тази стойност. Той смята, че нивото на α трябва да се установи в съответствие с конкретни обстоятелства. Например във физиката на частиците тя е 0,01.
Статистическото ниво на р
Терминът p-стойност е използван за първи път в работата на Браунли през 1960 година. Р-ниво (p-стойност) е показател, който е обратно свързан с истинността на резултатите. Най-високият коефициент p-стойност съответства на най-ниското ниво на увереност в извадката на зависимост между променливите.
Тази стойност отразява вероятността от грешки, свързани с интерпретацията на резултатите. Да предположим, p-ниво = 0,05 (1/20). Показва вероятността от пет процента, че връзката между променливите, открити в извадката, е просто случайна характеристика на извадката.Тоест, ако тази зависимост отсъства, тогава при повторни такива експерименти, средно във всяко двадесето изследване, може да се очаква една и съща или по-голяма зависимост между променливите. Често p-нивото се счита за „приемлив марж“ на нивото на грешка.
Между другото, p-стойността може да не отразява реалната връзка между променливите, а показва само определена средна стойност в рамките на предположенията. По-специално, крайният анализ на данните също ще зависи от избраните стойности на този коефициент. С p-ниво = 0,05 ще има някои резултати, а с коефициент 0,01, други.
Тестване на статистически хипотези
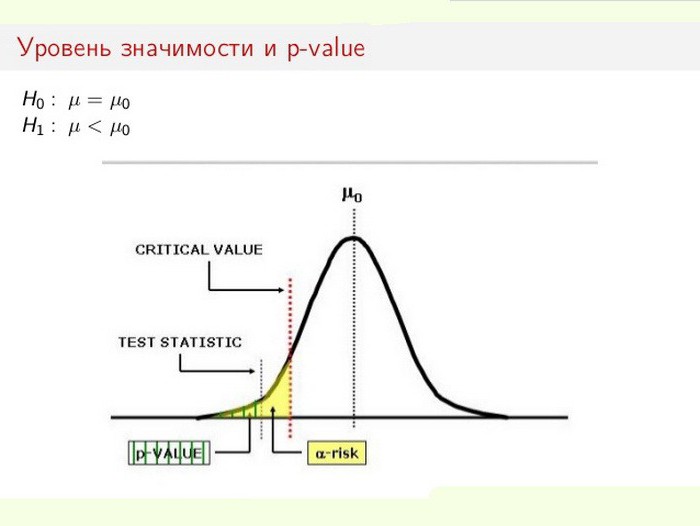
Нивото на статистическа значимост е особено важно при тестване на хипотези. Например, при изчисляване на двустранен тест, зоната на отхвърляне се разделя по равно на двата края на разпределението на извадката (спрямо нулевата координата) и се изчислява истинността на данните.
Да предположим, че при наблюдение на определен процес (явление) се оказа, че новата статистическа информация показва малки промени спрямо предходните стойности. Освен това, несъответствията в резултатите са малки, не са очевидни, но са важни за изследването. Дилемата възниква пред специалиста: наистина ли се случват промени или това са грешки в извадката (неточни измервания)?
В този случай нулевата хипотеза се използва или отхвърля (всички се приписват на грешка или промяната в системата се разпознава като fait comppli). Процесът на решаване на проблема се основава на съотношението на общата статистическа значимост (p-стойност) и ниво на значимост (α). Ако p-ниво <α, нулевата хипотеза се отхвърля. Колкото по-малка е р-стойността, толкова по-значима е тестовата статистика.
Използвани стойности
Нивото на значимост зависи от материала, който се анализира. На практика се използват следните фиксирани стойности:
- α = 0,1 (или 10%);
- α = 0,05 (или 5%);
- α = 0.01 (или 1%);
- α = 0,001 (или 0,1%).
Колкото по-точни са необходими изчисленията, толкова по-нисък е използван коефициентът α. Естествено, статистическите прогнози във физиката, химията, фармацевтиката, генетиката изискват по-голяма точност, отколкото в политологията, социологията.

Прагове на значение в конкретни области
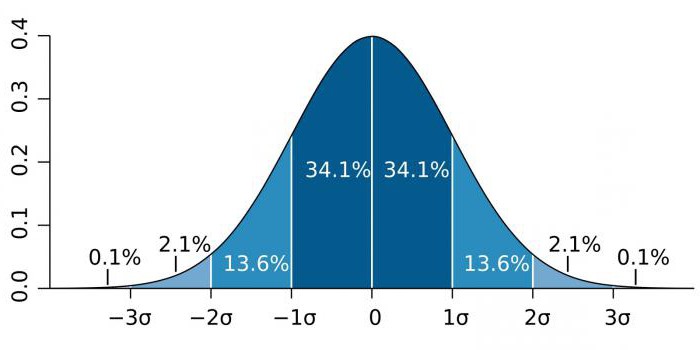
В области с висока точност, като физика на частиците и производствени дейности, статистическата значимост често се изразява като съотношение на стандартното отклонение (обозначено със сигма-коефициент - σ) спрямо нормалното разпределение на вероятността (гауссово разпределение). σ е статистически индикатор, който определя дисперсията на стойностите на определена стойност спрямо математическите очаквания. Използва се за очертаване на вероятността от събития.
В зависимост от областта на знанието, коефициентът σ варира значително. Например, когато се предвижда съществуването на бозона на Хигс, параметърът σ е пет (σ = 5), което съответства на стойността p-стойност = 1 / 3,5 милиона.При изследвания на геноми нивото на значимост може да бъде 5 × 10-8които не са рядкост за тази област.
ефикасност
Имайте предвид, че коефициентите α и p-стойност не са точни характеристики. Каквото и да е нивото на значимост в статистиката на изследваното явление, това не е безусловна основа за приемане на хипотезата. Например, колкото по-малка е стойността на α, толкова по-голям е шансът, че установената хипотеза е значителна. Съществува обаче риск от грешка, което намалява статистическата сила (значимост) на изследването.
Изследователите, които се фокусират единствено върху статистически значимите резултати, могат да получат грешни заключения. В същото време е трудно да се провери двойно тяхната работа, тъй като те използват предположения (които всъщност са стойностите на α и p-стойност). Затова винаги се препоръчва, заедно с изчисляването на статистическата значимост, да се определи друг показател - величината на статистическия ефект. Големината на ефекта е количествена мярка за силата на ефекта.
