Το επίπεδο σημαντικότητας στις στατιστικές είναι ένας σημαντικός δείκτης που αντικατοπτρίζει τον βαθμό εμπιστοσύνης στην ακρίβεια και την αλήθεια των λαμβανόμενων (προβλεπόμενων) δεδομένων. Η έννοια αυτή χρησιμοποιείται ευρέως σε διάφορους τομείς: από τη διεξαγωγή κοινωνιολογικής έρευνας έως τη στατιστική δοκιμασία επιστημονικών υποθέσεων.

Ορισμός
Το επίπεδο στατιστικής σημασίας (ή στατιστικά σημαντικό αποτέλεσμα) δείχνει ποια είναι η πιθανότητα τυχαίας εμφάνισης των μελετών που έχουν μελετηθεί. Η γενική στατιστική σημασία του φαινομένου εκφράζεται από τον συντελεστή p-value (ρ-επίπεδο). Σε οποιοδήποτε πείραμα ή παρατήρηση, είναι πιθανό τα ληφθέντα δεδομένα να οφείλονται σε σφάλματα δειγματοληψίας. Αυτό ισχύει ιδιαίτερα για την κοινωνιολογία.
Δηλαδή, ένα στατιστικό είναι στατιστικά σημαντικό, του οποίου η πιθανότητα τυχαίας εμφάνισης είναι εξαιρετικά μικρή ή τείνει στα άκρα. Το άκρο σε αυτό το πλαίσιο θεωρείται ο βαθμός απόκλισης των στατιστικών από την μηδενική υπόθεση (υπόθεση που ελέγχεται για συνέπεια με τα ληφθέντα δείγματα δεδομένων). Στην επιστημονική πρακτική, το επίπεδο σημασίας επιλέγεται πριν από τη συλλογή δεδομένων και, κατά κανόνα, ο συντελεστής του είναι 0,05 (5%). Για συστήματα όπου οι ακριβείς τιμές είναι εξαιρετικά σημαντικές, ο δείκτης αυτός μπορεί να είναι 0,01 (1%) ή μικρότερος.
Ιστορικό
Η έννοια του επιπέδου σπουδαιότητας εισήχθη από τον Βρετανό στατιστικολόγο και γενετιστή Ρόναλντ Φίσερ το 1925, όταν ανέπτυξε μια μεθοδολογία για τη δοκιμή στατιστικών υποθέσεων. Όταν αναλύεται μια διαδικασία, υπάρχει κάποια πιθανότητα ορισμένων φαινομένων. Δυσχέρειες προκύπτουν όταν εργάζεστε με μικρές (ή όχι προφανείς) πιθανότητες που εμπίπτουν στην έννοια του "σφάλματος μέτρησης".
Όταν εργάζονται με στατιστικά στοιχεία που δεν είναι αρκετά συγκεκριμένα για να επαληθεύσουν, οι επιστήμονες αντιμετώπιζαν το πρόβλημα της μηδενικής υπόθεσης, η οποία «παρεμβαίνει» με μικρές ποσότητες. Ο Fisher πρότεινε να οριστούν για τέτοια συστήματα πιθανότητα γεγονότων 5% (0,05) ως μια κατάλληλη επιλεκτική φέτα, επιτρέποντάς σας να απορρίψετε την μηδενική υπόθεση στους υπολογισμούς.
Η εισαγωγή ενός σταθερού συντελεστή
Το 1933, οι επιστήμονες Jerzy Neumann και Egon Pearson στα έργα τους συνιστούσαν εκ των προτέρων (πριν από τη συλλογή δεδομένων) να καθορίσουν ένα ορισμένο επίπεδο σπουδαιότητας. Παραδείγματα χρήσης αυτών των κανόνων είναι σαφώς ορατά κατά τη διάρκεια των εκλογών. Ας υποθέσουμε ότι υπάρχουν δύο υποψήφιοι, ένας από τους οποίους είναι πολύ δημοφιλής και ο δεύτερος είναι ελάχιστα γνωστός. Προφανώς, ο πρώτος υποψήφιος κερδίζει τις εκλογές και οι πιθανότητες του δεύτερου τείνουν στο μηδέν. Αγωνίζονται - αλλά όχι ίσοι: υπάρχει πάντα η πιθανότητα ανωτέρας βίας, συγκλονιστικές πληροφορίες, απροσδόκητες αποφάσεις που μπορούν να αλλάξουν τα προβλεπόμενα αποτελέσματα των εκλογών.
Οι Neumann και Pearson συμφώνησαν ότι το προτεινόμενο από το Fisher επίπεδο σπουδαιότητας 0,05 (που υποδηλώνεται με το σύμβολο α) είναι πιο βολικό. Ωστόσο, ο ίδιος ο Φίσερ το 1956 αντιτάχθηκε στη σταθεροποίηση αυτής της αξίας. Πιστεύει ότι το επίπεδο α πρέπει να καθοριστεί σύμφωνα με συγκεκριμένες περιστάσεις. Για παράδειγμα, στη φυσική των σωματιδίων είναι 0,01.
P-value
Ο όρος p-value χρησιμοποιήθηκε για πρώτη φορά στο έργο του Brownley το 1960. Το επίπεδο P (p-value) είναι ένας δείκτης που αντιστρόφως σχετίζεται με την αλήθεια των αποτελεσμάτων. Η υψηλότερη τιμή ρ του συντελεστή αντιστοιχεί στο χαμηλότερο επίπεδο εμπιστοσύνης στο δείγμα εξάρτησης μεταξύ των μεταβλητών.
Αυτή η τιμή αντικατοπτρίζει την πιθανότητα σφαλμάτων που σχετίζονται με την ερμηνεία των αποτελεσμάτων. Υποθέστε p-επίπεδο = 0,05 (1/20). Δείχνει την πιθανότητα πέντε τοις εκατό ότι η σχέση μεταξύ των μεταβλητών που βρέθηκαν στο δείγμα είναι απλώς ένα τυχαίο χαρακτηριστικό του δείγματος.Δηλαδή, αν αυτή η εξάρτηση απουσιάζει, τότε με επανειλημμένα πειράματα, κατά μέσο όρο, σε κάθε εικοστή μελέτη, μπορεί κανείς να αναμένει την ίδια ή μεγαλύτερη εξάρτηση μεταξύ των μεταβλητών. Συχνά, το επίπεδο p θεωρείται ως το "αποδεκτό περιθώριο" του επιπέδου σφάλματος.
Παρεμπιπτόντως, η τιμή ρ μπορεί να μην αντανακλά την πραγματική σχέση μεταξύ των μεταβλητών, αλλά δείχνει μόνο μια συγκεκριμένη μέση τιμή μέσα στις παραδοχές. Συγκεκριμένα, η τελική ανάλυση των δεδομένων θα εξαρτηθεί επίσης από τις επιλεγμένες τιμές αυτού του συντελεστή. Με p-επίπεδο = 0,05, θα υπάρξουν κάποια αποτελέσματα, και με ένα συντελεστή 0,01, άλλα.
Δοκιμές στατιστικών υποθέσεων
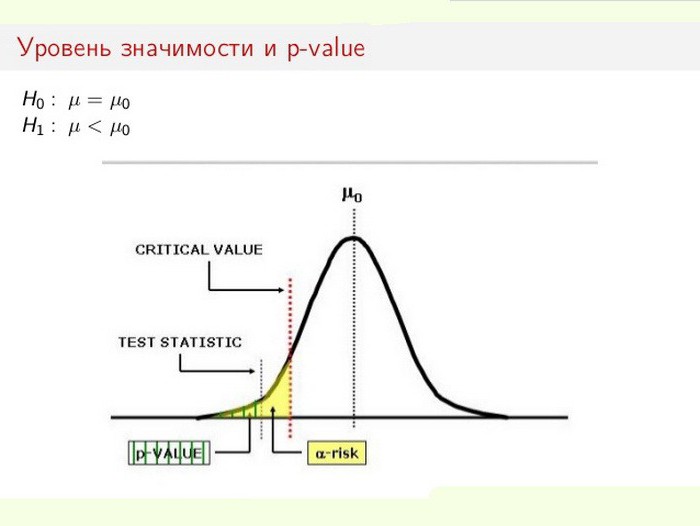
Το επίπεδο στατιστικής σημασίας είναι ιδιαίτερα σημαντικό όταν δοκιμάζουμε υποθέσεις. Για παράδειγμα, κατά τον υπολογισμό μιας δοκιμασίας δύο όψεων, η περιοχή απόρριψης διαιρείται εξίσου και στα δύο άκρα της κατανομής του δείγματος (σε σχέση με τη μηδενική συντεταγμένη) και υπολογίζεται η αλήθεια των δεδομένων.
Ας υποθέσουμε ότι, κατά την παρακολούθηση μιας συγκεκριμένης διαδικασίας (φαινόμενο), αποδείχθηκε ότι οι νέες στατιστικές πληροφορίες υποδεικνύουν μικρές αλλαγές σε σχέση με τις προηγούμενες τιμές. Επιπλέον, οι διαφορές στα αποτελέσματα είναι μικρές, όχι προφανείς, αλλά σημαντικές για τη μελέτη. Το δίλημμα εμφανίζεται πριν από τον ειδικό: συμβαίνουν αλλαγές πραγματικά ή είναι αυτά τα σφάλματα δειγματοληψίας (ανακριβείς μετρήσεις);
Σε αυτή την περίπτωση, η μηδενική υπόθεση χρησιμοποιείται ή απορρίπτεται (όλα αποδίδονται σε σφάλμα ή η αλλαγή στο σύστημα αναγνωρίζεται ως τετελεσμένη πρόκληση). Η διαδικασία επίλυσης του προβλήματος βασίζεται στην αναλογία της συνολικής στατιστικής σημασίας (p-value) και του επιπέδου σπουδαιότητας (α). Εάν το p-επίπεδο <α, τότε η μηδενική υπόθεση απορρίπτεται. Όσο μικρότερη είναι η τιμή p, τόσο πιο σημαντική είναι η στατιστική δοκιμασία.
Χρησιμοποιούμενες τιμές
Το επίπεδο σπουδαιότητας εξαρτάται από το υλικό που αναλύεται. Στην πράξη, χρησιμοποιούνται οι ακόλουθες σταθερές τιμές:
- α = 0,1 (ή 10%).
- α = 0,05 (ή 5%).
- α = 0,01 (ή 1%).
- α = 0,001 (ή 0,1%).
Όσο πιο ακριβείς είναι οι υπολογισμοί, τόσο χαμηλότερος χρησιμοποιείται ο συντελεστής α. Φυσικά, οι στατιστικές προβλέψεις στη φυσική, τη χημεία, τα φαρμακευτικά προϊόντα και τη γενετική απαιτούν μεγαλύτερη ακρίβεια απ 'ό, τι στην πολιτική επιστήμη, την κοινωνιολογία.

Σχετικά όρια σε συγκεκριμένους τομείς
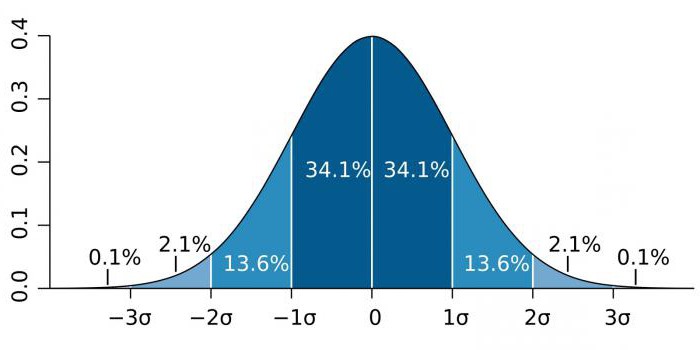
Σε περιοχές υψηλής ακρίβειας, όπως η φυσική των σωματιδίων και οι κατασκευαστικές δραστηριότητες, η στατιστική σημασία συχνά εκφράζεται ως ο λόγος της τυπικής απόκλισης (που υποδηλώνεται από τον συντελεστή σίγμα - σ) σε σχέση με την κανονική κατανομή πιθανότητας (Gaussian distribution). σ είναι ένας στατιστικός δείκτης που καθορίζει τη διασπορά τιμών μιας συγκεκριμένης τιμής σε σχέση με τις μαθηματικές προσδοκίες. Χρησιμοποιείται για να σχεδιαστεί η πιθανότητα γεγονότων.
Ανάλογα με το πεδίο γνώσης, ο συντελεστής σ ποικίλλει σημαντικά. Για παράδειγμα, όταν προβλέπουμε την ύπαρξη του μποζόνιο Higgs, η παράμετρος σ είναι πέντε (σ = 5), που αντιστοιχεί στην τιμή p value = 1 / 3,5 εκατομμύριο.Σε μελέτες γονιδιώματος το επίπεδο σημαντικότητας μπορεί να είναι 5 χ 10-8που δεν είναι ασυνήθιστο για αυτόν τον τομέα.
Αποτελεσματικότητα
Λάβετε υπόψη ότι οι συντελεστές α και p δεν είναι ακριβή χαρακτηριστικά. Όποιο και αν είναι το επίπεδο σημασίας στα στατιστικά στοιχεία του μελετώμενου φαινομένου, δεν αποτελεί μια άνευ όρων βάση για την αποδοχή της υπόθεσης. Για παράδειγμα, όσο μικρότερη είναι η τιμή του α, τόσο μεγαλύτερη είναι η πιθανότητα ότι η καθιερωμένη υπόθεση είναι σημαντική. Ωστόσο, υπάρχει κίνδυνος σφάλματος, ο οποίος μειώνει τη στατιστική ισχύ (σπουδαιότητα) της μελέτης.
Οι ερευνητές που επικεντρώνονται αποκλειστικά σε στατιστικά σημαντικά αποτελέσματα μπορεί να πάρουν εσφαλμένα συμπεράσματα. Ταυτόχρονα, είναι δύσκολο να ελέγξουμε τη δουλειά τους, διότι χρησιμοποιούν υποθέσεις (οι οποίες στην πραγματικότητα είναι οι τιμές α και p). Ως εκ τούτου, συνιστάται πάντα, μαζί με τον υπολογισμό της στατιστικής σημασίας, να προσδιοριστεί ένας άλλος δείκτης - το μέγεθος της στατιστικής επίδρασης. Το μέγεθος ενός αποτελέσματος είναι ένα ποσοτικό μέτρο της ισχύος μιας επίδρασης.
