Στο άρθρο θα εξετάσουμε την έννοια της "πιθανότητας ενός τυχαίου συμβάντος". Είναι γνωστό ότι σε διάφορες σφαίρες της ανθρώπινης δραστηριότητας υπάρχουν φαινόμενα που δεν μπορούν να προβλεφθούν με ακρίβεια. Έτσι, για παράδειγμα, ο όγκος των πωλήσεων των προϊόντων εξαρτάται τόσο από τις πολύ μεταβαλλόμενες ανάγκες των πελατών όσο και από άλλες αποχρώσεις που δεν είναι δυνατόν να ληφθούν υπόψη. Αυτός είναι ο λόγος για τον οποίο, δημιουργώντας παραγωγή και πραγματοποιώντας πωλήσεις, οι ιδιοκτήτες πρέπει να προβλέψουν τα αποτελέσματα των δραστηριοτήτων τους είτε με βάση την προσωπική τους εμπειρία είτε με μια παρόμοια ικανότητα άλλων ανθρώπων.
Για να αξιολογηθεί το εν λόγω γεγονός, είναι απαραίτητο να ληφθούν υπόψη ή να δημιουργηθούν ειδικά οι συνθήκες υπό τις οποίες καταγράφεται. Τέτοιες ενέργειες ονομάζονται εμπειρία ή πείραμα. Στη διαδικασία του, υπάρχουν πιθανά επεισόδια που ονομάζονται τυχαία, αν τελικά μπορούν να λάβουν χώρα ή όχι, καθώς και αξιόπιστα φαινόμενα που προκύπτουν ως αποτέλεσμα της πρακτικής.
Μελετάμε την πιθανότητα ενός γεγονότος χρησιμοποιώντας παραδείγματα. Για παράδειγμα, η χιονόπτωση στη Μόσχα στις 25 Νοεμβρίου θεωρείται τυχαίο επεισόδιο. Η καθημερινή ανατολή είναι ένα αξιόπιστο φαινόμενο και η χιονόπτωση στον ισημερινό του χιονιού θεωρείται αδύνατη περιέργεια. Ένα από τα πιο σημαντικά καθήκοντα στην θεωρία των πιθανοτήτων είναι το πρόβλημα του προσδιορισμού ποσοτικού μέτρου της πιθανότητας εμφάνισης ενός γεγονότος.
Πιθανότητα
Πιθανότητα είναι ο βαθμός (ποσοτική αξιολόγηση, σχετικό μέτρο) της πιθανότητας εμφάνισης ενός συμβάντος. Όταν οι λόγοι για ένα πιθανό περιστατικό στην πραγματικότητα αντισταθμίζονται από αντιφατικά επιχειρήματα, η υπόθεση αυτή λέγεται πιθανή. Διαφορετικά, λέγεται αμφίβολη ή απίστευτη.
Η υπεροχή της αρνητικής βάσης στη θετική και αντίστροφα μπορεί να είναι σε διάφορους βαθμούς, εξαιτίας των οποίων το απαράδεκτο (ή το παραδεκτό) είναι μικρότερο ή μεγαλύτερο. Για το λόγο αυτό, η πιθανότητα ενός γεγονότος συχνά γίνεται αντιληπτή σε επίπεδο πρώτης τάξης, ειδικά σε εκείνα τα περάσματα όπου είναι εξαιρετικά δύσκολο ή αδύνατο να δοθεί ακριβής ποσοτική εκτίμηση. Φυσικά, είναι δυνατές διάφορες διαβαθμίσεις των επιπέδων τυχόν.
Ανάλυση πιθανοτήτων
Παρεμπιπτόντως, η πιθανότητα ανεξάρτητων γεγονότων έχει ειδικές παραμέτρους. Και η ανίχνευση μιας πιθανότητας από μια μαθηματική θέση συμπληρώνει μια συγκεκριμένη πειθαρχία - θεωρία πιθανοτήτων. Σε αυτές τις διδακτικές και μαθηματικές στατιστικές, η έννοια του παραδεκτού χαρακτηρίζεται ως αριθμητική περιγραφή του επεισοδίου (ένα πιθανοτικό μέτρο ή το νόημά του).
Στην πραγματικότητα, αυτό είναι ένα μέτρο σε πολλές περιπτώσεις (υποσύνολα πολλών στοιχειωδών φαινομένων), που αποκτούν τιμές από 0 έως 1:
- μια τιμή 1 αντιστοιχεί σε ένα έγκυρο επεισόδιο.
- ένα αδύνατο γεγονός έχει μηδενική πιθανότητα (το αντίστροφο είναι σχεδόν πάντα ψευδές).
Εάν η εμφάνιση του φαινομένου είναι p, τότε ο κίνδυνος αδράνειας είναι 1-p. Πείτε, πιθανότητα ½ σημαίνει την ίδια πιθανότητα εμφάνισης και μη εμφάνισης της υπόθεσης.

Δήλωση Ευκαιρίας
Δοκιμή, συμβάν, πιθανότητα - αυτές οι μεταβλητές συνδέονται στενά με την επιστήμη. Ένας τυπικός ορισμός της τύχης βασίζεται στην έννοια της ευελιξίας των αποτελεσμάτων.
Ο λόγος του αριθμού των τελικών που συνεισφέρουν σε αυτό το γεγονός με τον συνολικό αριθμό εξίσου πιθανών τελικών είναι μια ευκαιρία. Παραδείγματος χάριν, το παραδεκτό μιας "ουράς" ή ενός "αετού" που πέφτει έξω εάν η ακούσια ανάληψη μιας δεκάρας είναι 1/2, αν υπολογίζεται ότι μόνο αυτές οι δύο διαδρομές είναι εξίσου πιθανές.

Αυτός ο κλασικός ορισμός της τύχης μπορεί να γενικευθεί στην περίπτωση ενός ανεξάντλητου αριθμού δυνητικών τιμών.Για παράδειγμα, εάν οποιοδήποτε φαινόμενο μπορεί να συμβεί με ίσο παραδεκτό σε οποιοδήποτε σημείο (ο αριθμός των σημείων είναι απεριόριστος) κάποιας τοπικής περιοχής του επιπέδου (χώρου), τότε ο κίνδυνος ότι θα συμβεί σε ένα ορισμένο μέρος αυτής της αποδεκτής σφαίρας αντιστοιχεί στην αναλογία της περιοχής (όγκου) στην περιοχή (όγκος) της περιοχής όλων των πιθανών σημείων.
Σύνδεσμος
Η πιθανότητα ενός γεγονότος μπορεί να προσδιοριστεί εμπειρικά. Αυτό οφείλεται στη συχνότητα εμφάνισης του επεισοδίου που βασίζεται στο γεγονός ότι με έναν εντυπωσιακό αριθμό δοκιμών, η συχνότητα πρέπει να επιδιώκει έναν αντικειμενικό βαθμό δυνατότητας αυτού του προηγουμένου.
Στην παρούσα παρουσίαση της θεωρίας πιθανοτήτων, η πιθανότητα αποκαλύπτεται axiomatically, ως ένα ιδιαίτερο γεγονός της αφηρημένης θεωρίας της μέτρησης ενός συνόλου. Εντούτοις, ανάμεσα στο παραδεκτό που εκφράζει το βαθμό της πραγματικότητας της εμφάνισης του φαινομένου και του αφηρημένου μέτρου, ο δεσμός είναι ακριβώς η συχνότητα της ανίχνευσής του.

Φυσικά, είναι πιθανή η πιθανότητα εμφάνισης ενός συμβάντος σε διάφορες διαδικασίες. Μια στοχαστική ερμηνεία ορισμένων φαινομένων είναι ευρέως διαδεδομένη στη σύγχρονη επιστήμη, ιδιαίτερα στην οικονομετρία, στη στατιστική φυσική των θερμοδυναμικών (ορατών) συστημάτων, όπου ακόμη και στην περίπτωση μιας αιτιοκρατικής κλασικής περιγραφής της κίνησης των σωματιδίων, μια συγκεκριμένη περιγραφή ολόκληρης της δομής τους δεν φαίνεται σκόπιμη και πρακτικά δυνατή. Στην κβαντική φυσική, οι ίδιες οι χαρακτηρισμένες διαδικασίες έχουν στοχαστικό χαρακτήρα.
Τυχαίο συμβάν
Φυσικά, η πιθανότητα εμφάνισης ενός συμβάντος σε κάθε ανεξέλεγκτη διαδικασία είναι υψηλή. Τι είναι ένα περιστατικό; Αυτό είναι ένα υποσύνολο των πολλών αποτελεσμάτων ενός τυχαίου πειράματος. Εάν μια τυχαία έρευνα επαναληφθεί πολλές φορές, η συχνότητα εμφάνισης ενός γεγονότος χρησιμεύει ως εκτίμηση του παραδεκτού της. 
Ένα ακούσιο φαινόμενο που δεν συμβαίνει ποτέ ως αποτέλεσμα ενός ακούσιου πειράματος αποκαλείται αδύνατο. Ένα τυχαίο επεισόδιο, το οποίο πραγματοποιείται πάντα ως αποτέλεσμα ενός απροσδόκητου πειράματος, ονομάζεται αξιόπιστο. Και πώς χαρακτηρίζεται η πιθανότητα ανεξάρτητων γεγονότων; Είναι γνωστό ότι δύο τυχαία γεγονότα ονομάζονται ανεξάρτητα εάν η εμφάνιση ενός από αυτά δεν αλλάζει το παραδεκτό της εμφάνισης του άλλου.
Ένα τυχαίο συμβάν είναι ένα κανονικό συμβάν που δημιουργείται δημιουργώντας ακούσιες λειτουργίες με υποκατάσταση τυχαίων μεταβλητών σε μεταβλητές. Η συνήθης λειτουργία της δημιουργίας ενός αριθμού λαχειοφόρων αγορών γίνεται με εργαλεία ηλεκτρονικών υπολογιστών.
Ορισμός
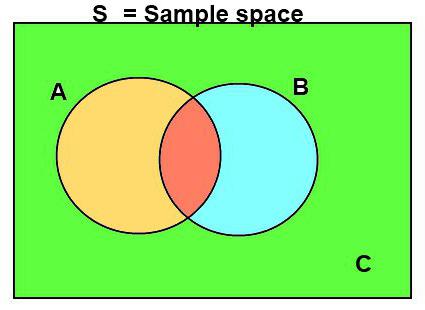
Ένα μαθηματικά τυχαίο επεισόδιο είναι ένα υποσύνολο του χώρου των στοιχειωδών αποτελεσμάτων μιας ακούσιας δοκιμής. Αυτό είναι ένα στοιχείο της σίγμα-άλγεβρας ή άλγεβρας-F, το οποίο με τη σειρά του τίθεται αυτονόητα και μαζί με το χώρο των απλούστερων φαινομένων "Ωμέγα" και η πιθανότητα Ρ σχηματίζει ένα χώρο πιθανότητας.
Ιστορικό της έννοιας της τύχης
Η πιθανότητα ενός τυχαίου γεγονότος έχει συχνά διερευνηθεί. Σε γενικές γραμμές, η εμφάνιση της έννοιας της τύχης έχει συσχετιστεί ιστορικά με τα τυχερά παιχνίδια, ειδικά τα ζάρια. Πριν από την εμφάνιση αυτής της έννοιας, περιγράφηκαν κυρίως τα συνδυαστικά καθήκοντα υπολογισμού του αριθμού δυνητικών αποτελεσμάτων κατά τη ρίψη ζευγαριών ζαριών, καθώς και το ζήτημα της διανομής των στοιχημάτων μεταξύ των συμμετεχόντων όταν το παιχνίδι τελείωσε πριν το χρονοδιάγραμμα.
Ο επίσκοπος Vibold της πόλης Cambrai το 960 αποφάσισε το πρώτο rebus όταν ρίχνει τρία ζάρια. Μετρούσε 56 είδη. Ωστόσο, αυτός ο αριθμός στην πραγματικότητα δεν αναπαράγει το άθροισμα των εξίσου δυνατών μεθόδων, επειδή κάθε μία από τις 56 εκδοχές τους μπορεί να πραγματοποιηθεί από διαφορετικό αριθμό δεξιώσεων.
Η πιθανότητα ενός τυχαίου γεγονότος μελετήθηκε στο πρώτο μισό του 13ου αιώνα από τον Richard de Fornival. Παρά το γεγονός ότι αναφέρει επίσης τον αριθμό 56, αντανακλά στη σκέψη ότι ο ίδιος αριθμός σημείων σε τρία οστά μπορεί να ληφθεί με έξι μεθόδους.
Βάσει των συλλογισμών του, είναι ήδη δυνατό να διαπιστωθεί ότι ο αριθμός των εξίσου προσβάσιμων επιλογών είναι 216. Στη συνέχεια, πολλοί δεν το λύσουν αρκετά σωστά.Για πρώτη φορά, ο Gallio Galilei υπολόγισε τον αριθμό των εξίσου προσβάσιμων αποτελεσμάτων όταν ρίχνει τρία οστά: έθεσε τους έξι (τον αριθμό των εκδοχών της απώλειας ενός οστού) στο βαθμό 3 (ο αριθμός των οστών). Επίσης, συνέταξε έναν πίνακα με τον αριθμό των επιλογών για την εξαγωγή διαφόρων ποσοτήτων σημείων.
Ελπίζουμε ότι το άρθρο μας θα σας εξοικειώσει με την πιθανότητα τυχαίου γεγονότος.








