El nivel de significancia en las estadísticas es un indicador importante que refleja el grado de confianza en la precisión y la verdad de los datos recibidos (pronosticados). El concepto es ampliamente utilizado en varios campos: desde la realización de investigaciones sociológicas, hasta la prueba estadística de hipótesis científicas.

Definición
El nivel de significación estadística (o resultado estadísticamente significativo) muestra cuál es la probabilidad de una ocurrencia accidental de los indicadores estudiados. La significación estadística general del fenómeno se expresa mediante el coeficiente p-valor (nivel p). En cualquier experimento u observación, es probable que los datos obtenidos se deban a errores de muestreo. Esto es especialmente cierto para la sociología.
Es decir, una estadística es estadísticamente significativa cuya probabilidad de ocurrencia accidental es extremadamente pequeña o tiende a extremos. Extremo en este contexto se considera el grado de desviación de las estadísticas de la hipótesis nula (una hipótesis que se verifica para verificar su coherencia con los datos de la muestra obtenida). En la práctica científica, el nivel de significancia se elige antes de la recopilación de datos y, por regla general, su coeficiente es 0.05 (5%). Para sistemas donde los valores precisos son extremadamente importantes, este indicador puede ser 0.01 (1%) o menos.
Antecedentes
El concepto de nivel de significancia fue introducido por el estadístico y genetista británico Ronald Fisher en 1925 cuando desarrolló una metodología para probar hipótesis estadísticas. Al analizar un proceso, hay una cierta probabilidad de ciertos fenómenos. Surgen dificultades cuando se trabaja con probabilidades de porcentaje pequeñas (o no obvias) que se enmarcan en el concepto de "error de medición".
Al trabajar con estadísticas que no son lo suficientemente específicas para verificar, los científicos se enfrentaron con el problema de la hipótesis nula, que "interfiere" con pequeñas cantidades. Fisher sugirió definir para tales sistemas probabilidad de eventos 5% (0.05) como una porción selectiva conveniente, que le permite rechazar la hipótesis nula en los cálculos.
La introducción de un coeficiente fijo
En 1933, los científicos Jerzy Neumann y Egon Pearson en sus trabajos recomendaron de antemano (antes de la recopilación de datos) establecer un cierto nivel de importancia. Los ejemplos del uso de estas reglas son claramente visibles durante la elección. Supongamos que hay dos candidatos, uno de los cuales es muy popular y el segundo es poco conocido. Obviamente, el primer candidato gana las elecciones, y las posibilidades del segundo tienden a cero. Se esfuerzan, pero no son iguales: siempre existe la probabilidad de fuerza mayor, información sensacional, decisiones inesperadas que pueden cambiar los resultados electorales predichos.
Neumann y Pearson coincidieron en que el nivel de significancia propuesto por Fisher de 0.05 (indicado por el símbolo α) es lo más conveniente. Sin embargo, el propio Fisher en 1956 se opuso a la fijación de este valor. Él creía que el nivel de α debería establecerse de acuerdo con circunstancias específicas. Por ejemplo, en física de partículas es 0.01.
Valor p
El término valor p se utilizó por primera vez en el trabajo de Brownley en 1960. El nivel P (valor p) es un indicador que está inversamente relacionado con la verdad de los resultados. El valor p del coeficiente más alto corresponde al nivel más bajo de confianza en la muestra de dependencia entre las variables.
Este valor refleja la probabilidad de errores asociados con la interpretación de los resultados. Suponga que p-level = 0.05 (1/20). Muestra la probabilidad del cinco por ciento de que la relación entre las variables encontradas en la muestra es solo una característica aleatoria de la muestra.Es decir, si esta dependencia está ausente, entonces, con tales experimentos repetidos, en promedio, en cada vigésimo estudio, uno puede esperar la misma o mayor dependencia entre las variables. A menudo, el nivel p se considera como el "margen aceptable" del nivel de error.
Por cierto, el valor p puede no reflejar la relación real entre las variables, sino que solo muestra un cierto valor promedio dentro de los supuestos. En particular, el análisis final de los datos también dependerá de los valores seleccionados de este coeficiente. Con un nivel de p = 0.05, habrá algunos resultados, y con un coeficiente de 0.01, otros.
Prueba de hipótesis estadísticas
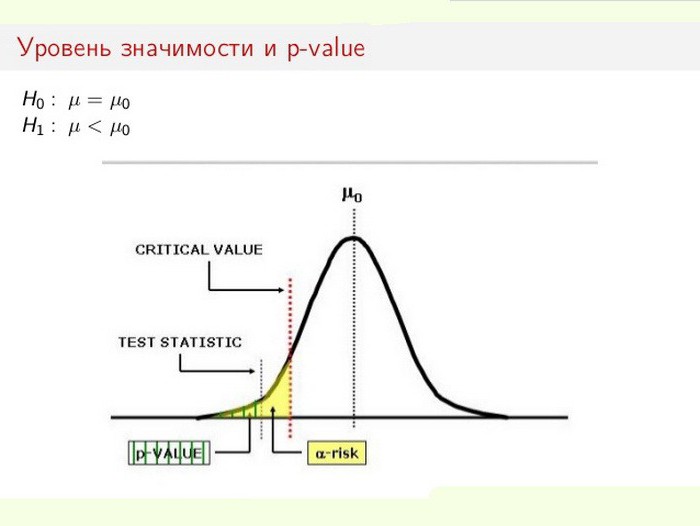
El nivel de significación estadística es especialmente importante cuando se prueban hipótesis. Por ejemplo, cuando se calcula una prueba de dos lados, el área de rechazo se divide por igual en ambos extremos de la distribución de la muestra (en relación con la coordenada cero) y se calcula la verdad de los datos.
Supongamos que, al monitorear un determinado proceso (fenómeno), resulta que la nueva información estadística indica pequeños cambios en relación con los valores anteriores. Además, las discrepancias en los resultados son pequeñas, no obvias, pero importantes para el estudio. El dilema surge ante el especialista: ¿realmente se están produciendo cambios o son estos errores de muestreo (mediciones inexactas)?
En este caso, se utiliza o rechaza la hipótesis nula (todo atribuido a un error, o el cambio en el sistema se reconoce como un hecho consumado). El proceso de resolución del problema se basa en la relación de significancia estadística total (valor p) y nivel de significancia (α). Si el nivel p <α, se rechaza la hipótesis nula. Cuanto más pequeño es el valor p, más significativo es el estadístico de prueba.
Valores utilizados
El nivel de significación depende del material que se analiza. En la práctica, se utilizan los siguientes valores fijos:
- α = 0.1 (o 10%);
- α = 0,05 (o 5%);
- α = 0.01 (o 1%);
- α = 0.001 (o 0.1%).
Cuanto más precisos sean los cálculos, menor será el coeficiente α. Naturalmente, los pronósticos estadísticos en física, química, farmacéutica y genética requieren una mayor precisión que en ciencias políticas, sociología.

Umbrales de relevancia en áreas específicas.
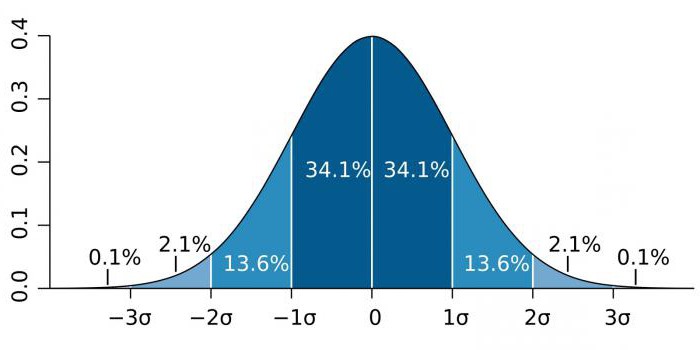
En áreas de alta precisión, como la física de partículas y las actividades de fabricación, la significación estadística a menudo se expresa como la relación de la desviación estándar (denotada por el coeficiente sigma - σ) en relación con la distribución de probabilidad normal (distribución gaussiana). σ es un indicador estadístico que determina la dispersión de valores de un determinado valor en relación con las expectativas matemáticas. Se usa para trazar la probabilidad de eventos.
Dependiendo del campo de conocimiento, el coeficiente σ varía mucho. Por ejemplo, al predecir la existencia del bosón de Higgs, el parámetro σ es cinco (σ = 5), que corresponde a un valor p = 1 / 3.5 millones. En los estudios de genomas, el nivel de significancia puede ser 5 × 10-8que no son infrecuentes para esta área.
Efectividad
Tenga en cuenta que los coeficientes α y valor p no son características precisas. Cualquiera que sea el nivel de significación en las estadísticas del fenómeno estudiado, no es una base incondicional para aceptar la hipótesis. Por ejemplo, cuanto menor es el valor de α, mayor es la posibilidad de que la hipótesis establecida sea significativa. Sin embargo, existe un riesgo de error, lo que reduce el poder estadístico (importancia) del estudio.
Los investigadores que se centran únicamente en resultados estadísticamente significativos pueden llegar a conclusiones erróneas. Al mismo tiempo, es difícil verificar su trabajo, ya que utilizan supuestos (que, de hecho, son los valores de los valores α y p). Por lo tanto, siempre se recomienda, junto con el cálculo de la significación estadística, determinar otro indicador: la magnitud del efecto estadístico. La magnitud de un efecto es una medida cuantitativa de la fuerza de un efecto.
