Tilastollisuuden merkitsevyystaso on tärkeä indikaattori, joka heijastaa luottamuksen tasoa vastaanotetun (ennustetun) tiedon tarkkuuteen ja totuuteen. Käsitettä käytetään laajalti eri aloilla: sosiologisen tutkimuksen suorittamisesta tieteellisten hypoteesien tilastolliseen testaamiseen.

määritelmä
Tilastollisen merkitsevyyden taso (tai tilastollisesti merkitsevä tulos) osoittaa, mikä on tutkittujen indikaattorien vahingossa tapahtuvan esiintymisen todennäköisyys. Ilmiön yleinen tilastollinen merkitys ilmaistaan kertoimella p-arvo (p-taso). Missä tahansa kokeessa tai havainnossa on todennäköistä, että saadut tiedot johtuvat näytteenottovirheistä. Tämä pätee erityisesti sosiologiaan.
Toisin sanoen tilasto on tilastollisesti merkitsevä, jonka vahingossa tapahtuvan esiintymisen todennäköisyys on erittäin pieni tai yleensä äärimmäinen. Äärimmäisenä pidetään tässä yhteydessä tilastojen poikkeamisastetta nollahypoteesista (hypoteesista, joka tarkistetaan johdonmukaisuuden suhteen saadun näytteen tietojen kanssa). Tieteellisessä käytännössä merkitsevyystaso valitaan ennen tiedonkeruua ja yleensä sen kerroin on 0,05 (5%). Järjestelmissä, joissa tarkat arvot ovat erittäin tärkeitä, tämä indikaattori voi olla 0,01 (1%) tai vähemmän.
sairauskertomus
Brittiläinen tilastotieteilijä ja geneetikko Ronald Fisher esitteli merkitsevyystason käsitteen vuonna 1925, kun hän kehitti menetelmän tilastollisten hypoteesien testaamiseksi. Prosessia analysoitaessa on tietty todennäköisyys tietyille ilmiöille. Vaikeuksia syntyy työskennellessä pienten (tai ei selvien) prosentuaalisten todennäköisyyksien kanssa, jotka kuuluvat käsitteeseen "mittausvirhe".
Työskennellessäsi tilastojen kanssa, jotka eivät ole riittävän täsmällisiä todentamiseksi, tutkijat kohtasivat nollahypoteesin ongelman, joka ”häiritsee” pieniä määriä. Fisher ehdotti tällaisten järjestelmien määrittelemistä tapahtumien todennäköisyys 5% (0,05) kätevänä selektiivisenä viipaleena, jonka avulla voit hylätä nollahypoteesin laskelmissa.
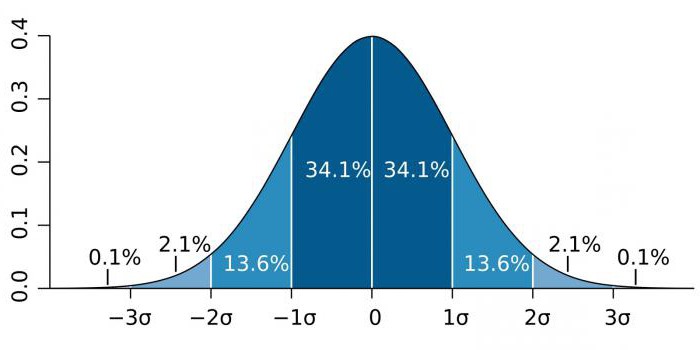
Kiinteän suhteen käyttöönotto
Vuonna 1933 tutkijat Jerzy Neumann ja Egon Pearson suosittelivat teoksissaan etukäteen (ennen tiedonkeruua) tietyn merkitystason saavuttamiseksi. Esimerkkejä näiden sääntöjen käytöstä näkyy selvästi vaalien aikana. Oletetaan, että ehdokkaita on kaksi, joista toinen on erittäin suosittu ja toinen on vähän tunnettu. Ensimmäinen ehdokas on selvästi voittanut vaalit, ja toisen ehdokkaat ovat yleensä nolla. He pyrkivät - mutta eivät yhtäläisesti: aina on mahdollista ylivoimainen este, sensaatiomainen tieto, odottamattomat päätökset, jotka voivat muuttaa ennustettuja vaalituloksia.
Neumann ja Pearson olivat yhtä mieltä siitä, että Fisherin ehdotettu merkitsevyystaso 0,05 (merkitty symbolilla α) on sopivin. Fisher itse vuonna 1956 kuitenkin vastusti tämän arvon vahvistamista. Hän katsoi, että α-taso olisi määritettävä erityisten olosuhteiden mukaisesti. Esimerkiksi hiukkasfysiikassa se on 0,01.
Merkitsevyystaso p-
Termiä p-arvo käytettiin ensimmäisen kerran Brownleyn työssä vuonna 1960. P-taso (p-arvo) on indikaattori, joka liittyy käänteisesti tulosten totuuteen. Suurin kerroin p-arvo vastaa alinta luotettavuustasoa muuttujien välisestä riippuvuudesta.
Tämä arvo heijastaa tulosten tulkintaan liittyvien virheiden todennäköisyyttä. Oletetaan, että p-taso = 0,05 (1/20). Se osoittaa viiden prosentin todennäköisyyden, että otoksesta löytyvien muuttujien välinen suhde on vain otoksen satunnainen piirre.Toisin sanoen, jos tätä riippuvuutta ei ole, niin toistuvilla sellaisilla kokeilla voidaan odottaa keskimäärin jokaisessa kahdeskymmennessä tutkimuksessa muuttujien välinen sama tai suurempi riippuvuus. Usein p-tasoa pidetään virhetason ”hyväksyttävänä marginaalina”.
Muuten, p-arvo ei ehkä heijasta muuttujien välistä todellista suhdetta, vaan näyttää vain tietyn keskiarvon oletusten sisällä. Erityisesti datan lopullinen analyysi riippuu myös tämän kertoimen valituista arvoista. Jos p-taso = 0,05, tuloksia on jonkin verran, ja kertoimella 0,01 muita.
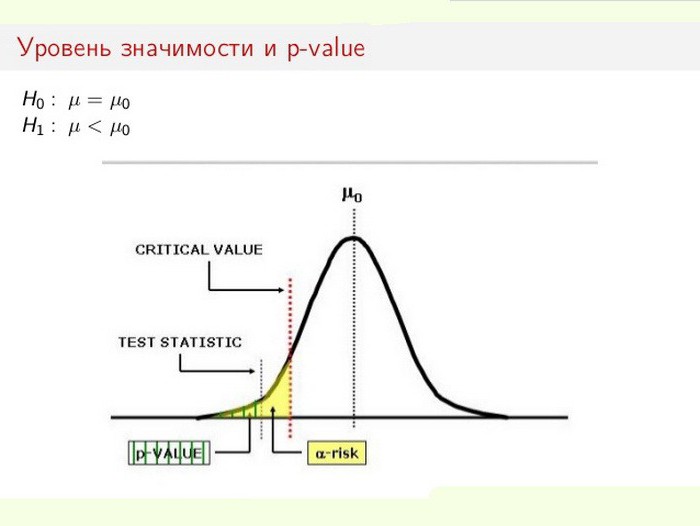
Tilastollisten hypoteesien testaaminen
Tilastollisen merkitsevyyden taso on erityisen tärkeä hypoteesien testaamisessa. Esimerkiksi laskettaessa kaksipuolista testiä, hylkäysalue jaetaan tasaisesti näytteen jakautumisen molemmissa päissä (suhteessa nollakoordinaattiin) ja lasketaan datan totuus.
Oletetaan, että tarkkailtaessa tiettyä prosessia (ilmiötä) kävi ilmi, että uusi tilastotieto osoittaa pieniä muutoksia suhteessa aikaisempiin arvoihin. Lisäksi tulosten väliset erot ovat pieniä, eivät selviä, mutta tärkeitä tutkimukselle. Dilemma syntyy ennen asiantuntijaa: tapahtuvatko muutokset todella vai ovatko nämä näytteenottovirheet (epätarkkoja mittauksia)?
Tässä tapauksessa nollahypoteesia joko käytetään tai hylätään (kaikki johtuu virheestä tai järjestelmän muutos tunnustetaan tosiasialliseksi suoritukseksi). Ongelman ratkaisuprosessi perustuu kokonaistilastollisuuden (p-arvo) ja merkitsevyystason (α) suhteeseen. Jos p-taso <α, nollahypoteesi hylätään. Mitä pienempi p-arvo, sitä merkitsevämpi on testitilasto.
Käytetyt arvot
Merkitysaste riippuu analysoitavasta materiaalista. Käytännössä käytetään seuraavia kiinteitä arvoja:
- a = 0,1 (tai 10%);
- a = 0,05 (tai 5%);
- a = 0,01 (tai 1%);
- a = 0,001 (tai 0,1%).
Mitä tarkempia laskelmia vaaditaan, sitä alhaisempaa kerrointa α käytetään. Luonnollisesti fysiikan, kemian, lääkkeiden ja genetiikan tilastolliset ennusteet vaativat suurempaa tarkkuutta kuin valtiotiede, sosiologia.

Merkitykselliset kynnysarvot tietyillä alueilla
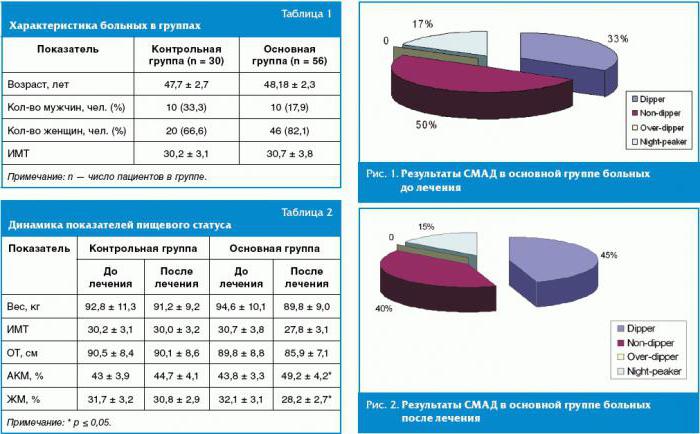
Erittäin tarkkoilla alueilla, kuten hiukkasfysiikka ja valmistustoiminnot, tilastollinen merkitsevyys ilmaistaan usein keskihajonnan suhteena (merkitty sigma-kertoimella - σ) suhteessa normaaliin todennäköisyysjakaumaan (Gaussin jakauma). σ on tilastollinen indikaattori, joka määrittää tietyn arvon hajonta suhteessa matemaattisiin odotuksiin. Käytetään tapahtumien todennäköisyyden piirtämiseen.
Tietokentästä riippuen kerroin σ vaihtelee suuresti. Esimerkiksi ennustaessasi Higgs-bosonin olemassaoloa, parametri σ on viisi (σ = 5), joka vastaa arvoa p-arvo = 1 / 3,5 miljoonaa. Genomitutkimuksissa merkitsevyystaso voi olla 5 × 10-8jotka eivät ole harvinaisia tällä alueella.
tehokkuuden
Muista, että kertoimet α ja p-arvo eivät ole tarkkoja ominaisuuksia. Riippumatta tutkitun ilmiön merkityksellisyystasosta, se ei ole ehdoton perusta hypoteesin hyväksymiselle. Esimerkiksi, mitä pienempi α-arvo, sitä suurempi on mahdollisuus, että vakiintunut hypoteesi on merkittävä. On kuitenkin olemassa virheriski, joka vähentää tutkimuksen tilastollista tehoa (merkitsevyyttä).
Tutkijat, jotka keskittyvät pelkästään tilastollisesti merkittäviin tuloksiin, voivat saada virheelliset johtopäätökset. Samanaikaisesti heidän työtä on vaikea tarkistaa, koska he käyttävät oletuksia (jotka tosiasiassa ovat α- ja p-arvot). Siksi on aina suositeltavaa määrittää tilastollisen merkitsevyyden laskemisen ohella toinen indikaattori - tilastollisen vaikutuksen suuruus. Vaikutuksen suuruus on vaikutuksen voimakkuuden kvantitatiivinen mitta.
