רמת המשמעות בסטטיסטיקה היא אינדיקטור חשוב המשקף את מידת הביטחון ברמת הדיוק והאמת של הנתונים שהתקבלו (חזויים). הרעיון נמצא בשימוש נרחב בתחומים שונים: החל מביצוע מחקר סוציולוגי, לבדיקה סטטיסטית של השערות מדעיות.

הגדרה
רמת המשמעות הסטטיסטית (או תוצאה משמעותית סטטיסטית) מראה מהי ההסתברות להתרחשות מקרית של המדדים שנחקרו. המשמעות הסטטיסטית הכללית של התופעה באה לידי ביטוי על ידי המקדם p-value (p-level). בכל ניסוי או תצפית כלשהי, סביר להניח שהנתונים שהושגו נובעים משגיאות דגימה. זה נכון במיוחד לסוציולוגיה.
כלומר, נתון הוא מובהק סטטיסטית שההסתברות שלו להתרחשות מקרית היא קטנה ביותר או נוטה לקיצוניות. קיצוני בהקשר זה נחשב למידת הסטייה של הסטטיסטיקה מהשערת האפס (השערה שנבדקת אם היא עולה בקנה אחד עם נתוני המדגם שהתקבלו). בפרקטיקה המדעית, נבחרת רמת המשמעות לפני איסוף הנתונים, וככלל המקדם שלה הוא 0.05 (5%). עבור מערכות בהן ערכים מדויקים חשובים ביותר, אינדיקטור זה יכול להיות 0.01 (1%) או פחות.
רקע
מושג רמת המשמעות הוצג על ידי הסטטיסטיקאי והגנטיקאי הבריטי רונלד פישר בשנת 1925 כאשר פיתח מתודולוגיה לבדיקת השערות סטטיסטיות. כאשר מנתחים תהליך, קיימת הסתברות מסוימת לתופעות מסוימות. קשיים מתעוררים בעבודה עם הסתברויות אחוז קטנות (או לא מובנות מאליהן) שנמצאות תחת המושג "שגיאת מדידה".
כשעבדו עם נתונים סטטיסטיים שאינם ספציפיים מספיק כדי לאמת, המדענים עמדו בפני הבעיה של השערת האפס, ש"הפריעה "לכמויות קטנות. פישר הציע להגדיר עבור מערכות כאלה הסתברות לאירועים 5% (0.05) כפרוסה סלקטיבית נוחה, המאפשרים לדחות את השערת האפס בחישובים.
הכנסת מקדם קבוע
בשנת 1933 המליצו המדענים ג'רזי נוימן ואגון פירסון בעבודותיהם מראש (לפני איסוף נתונים) לקבוע רמה מסוימת של משמעות. דוגמאות לשימוש בכללים אלה נראות בבירור במהלך הבחירות. נניח שיש שני מועמדים, אחד מהם פופולרי מאוד, והשני מעט ידוע. ברור שהמועמד הראשון זוכה בבחירות, והסיכויים לשני נוטים לאפס. הם שואפים - אך לא שווים: תמיד קיימת אפשרות לכוח עליון, מידע סנסציוני, החלטות בלתי צפויות שיכולות לשנות את תוצאות הבחירות החזויות.
נוימן ופירסון הסכימו שרמת המשמעות המוצעת של פישר של 0.05 (המסומנת בסמל α) היא הנוחה ביותר. עם זאת, פישר עצמו בשנת 1956 התנגד לקיבוע של ערך זה. הוא האמין כי יש לקבוע את רמת α בהתאם לנסיבות הספציפיות. לדוגמה, בפיזיקת החלקיקים זה 0.01.
ערך P
המונח p-value שימש לראשונה בעבודתו של בראונלי בשנת 1960. רמת P (ערך p) היא אינדיקטור שקשור הפוך לאמת התוצאות. ערך ה- p המקדם הגבוה ביותר תואם את רמת האמון הנמוכה ביותר במדגם התלות בין המשתנים.
ערך זה משקף את ההסתברות לטעויות הקשורות לפרשנות התוצאות. נניח ש- p-level = 0.05 (1/20). זה מראה את ההסתברות של חמישה אחוזים שהקשר בין המשתנים שנמצאו במדגם הוא רק מאפיין אקראי של המדגם.כלומר, אם תלות זו נעדרת, אז בעזרת ניסויים כאלה חוזרים, בממוצע, בכל מחקר עשרים, ניתן לצפות לתלות זהה או גדולה יותר בין המשתנים. לעתים קרובות, רמת ה- p נחשבת ל"מרווח המקובל "של רמת השגיאה.
אגב, ערך p עשוי לא לשקף את הקשר האמיתי בין המשתנים, אלא רק מראה ערך ממוצע מסוים בתוך ההנחות. בפרט, הניתוח הסופי של הנתונים יהיה תלוי גם בערכים שנבחרו של מקדם זה. עם רמת p = 0.05, יהיו תוצאות מסוימות ועם מקדם 0.01, אחרות.
בדיקת השערות סטטיסטיות
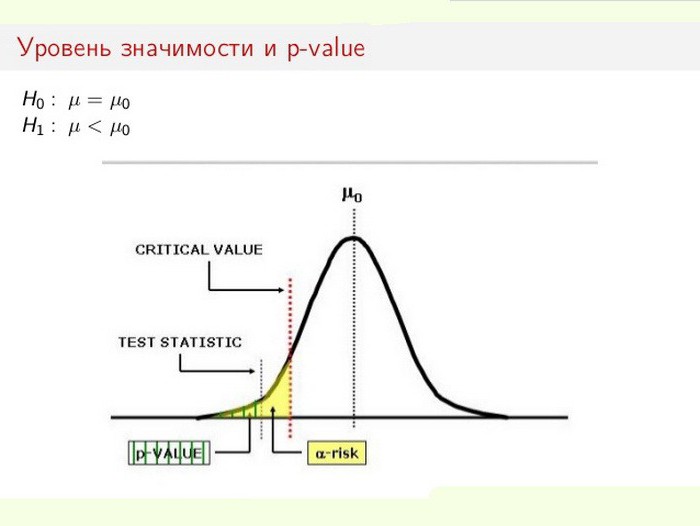
רמת המשמעות הסטטיסטית חשובה במיוחד בבדיקת השערות. לדוגמה, בעת חישוב מבחן דו-צדדי, אזור הדחייה מחולק באופן שווה בשני קצוות חלוקת המדגם (ביחס לקואורדינטת האפס) ומחושבים את אמיתות הנתונים.
נניח שבמעקב אחר תהליך מסוים (תופעה) התברר כי המידע הסטטיסטי החדש מצביע על שינויים קטנים ביחס לערכים הקודמים. יתר על כן, הפערים בתוצאות הם קטנים, לא ברורים, אך חשובים למחקר. הדילמה מתעוררת לפני המומחה: האם השינויים באמת מתרחשים או שמא שגיאות דגימה (מדידות לא מדויקות)?
במקרה זה, השערת האפס משמשת או נדחית (הכל מיוחס לטעות, או שהשינוי במערכת מוכר כעובדה מוגמרת). תהליך פיתרון הבעיה מבוסס על היחס בין המשמעות הסטטיסטית הכוללת (ערך p) ורמת המשמעות (α). אם רמת p <α, אז ההשערה האפסית נדחית. ככל שערך ה- p קטן יותר, כך נתון המבחן משמעותי יותר.
ערכים בשימוש
רמת המשמעות תלויה בחומר המנותח. בפועל משתמשים בערכים הקבועים הבאים:
- α = 0.1 (או 10%);
- α = 0.05 (או 5%);
- α = 0.01 (או 1%);
- α = 0.001 (או 0.1%).
ככל שנדרשים החישובים מדויקים יותר, כך נעשה שימוש במקדם α. באופן טבעי, תחזיות סטטיסטיות בפיזיקה, כימיה, תרופות, גנטיקה דורשות דיוק רב יותר מאשר במדע המדינה, בסוציולוגיה.

סף רלוונטיות בתחומים ספציפיים
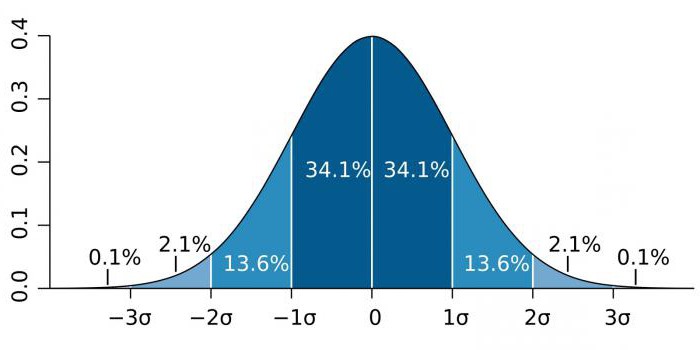
באזורים בעלי דיוק גבוה, כגון פיזיקת חלקיקים ופעילות ייצור, משמעות סטטיסטית מתבטאת לרוב ביחס לסטיית התקן (המצוינת במקדם sigma - σ) ביחס להתפלגות ההסתברות הרגילה (התפלגות גאוסית). σ הוא אינדיקטור סטטיסטי שקובע את פיזור הערכים של ערך מסוים ביחס לציפיות המתמטיות. משמש לעלילת ההסתברות לאירועים.
בהתאם לתחום הידע, המקדם σ משתנה מאוד. לדוגמה, כאשר חוזים את קיומו של בוזון היגס, הפרמטר σ הוא חמש (σ = 5), התואם לערך p-value = 1 / 3.5 מיליון. במחקרים על גנים, רמת המשמעות יכולה להיות 5 × 10-8שאינם נדירים בתחום זה.
אפקטיביות
קחו בחשבון שהמקדמים α וערך ה- p אינם מאפיינים מדויקים. תהיה אשר תהיה רמת המשמעות בסטטיסטיקה של התופעה הנחקרת, אין זה בסיס ללא תנאי לקבל את ההשערה. לדוגמא, ככל שערך α קטן יותר, כך גדל הסיכוי שההשערה שנקבעה היא משמעותית. עם זאת, קיים סיכון לטעות, מה שמפחית את העוצמה הסטטיסטית (משמעות) של המחקר.
חוקרים המתמקדים אך ורק בתוצאות בעלות משמעות סטטיסטית עשויים להגיע למסקנות שגויות. יחד עם זאת, קשה לבדוק מחדש את עבודתם, מכיוון שהם משתמשים בהנחות (שהן, למעשה, α ו- p-value). לכן, תמיד מומלץ, יחד עם חישוב המשמעות הסטטיסטית, לקבוע אינדיקטור אחר - גודל האפקט הסטטיסטי. גודל האפקט הוא מדד כמותי לחוזק האפקט.
